зҡ„зә§ж•°ж–№зЁӢ пјҢ 其收ж•ӣйҖҹеәҰжӣҙеҝ« гҖӮ иҜқиҜҙд»–еңЁеҚ°еәҰзӢ¬з«Ӣе·ҘдҪңж—¶е°ұжҸҗеҮәдәҶи®ёеӨҡж–°йў–зҡ„и®Ўз®— зҡ„ж•°еҲ— пјҢ иҖҢеҪ“д»–иҝңжёЎйҮҚжҙӢеҺ»еҫҖеү‘жЎҘжүҖжҗәеёҰзҡ„дёҖдёӘ笔记жң¬йҮҢе°ұжңүж•ҙж•ҙ 400 йЎөйғҪжҳҜе…ідәҺ зҡ„еҶ…е®№ гҖӮ
>
科жҠҖзҡ„иҝӣжӯҘ пјҢ йҡҸзқҖжңәжў°и®Ўз®—жңәиҜһз”ҹд№ӢеҗҺ пјҢ ж•°еӯҰ家们е°ұиҝ«дёҚеҸҠеҫ…еҲ©з”Ёиҝҷз§Қж–°ејҸе·Ҙе…·еә”з”ЁиҺұеёғе°је…№е…¬ејҸгҖҒ欧жӢүе…¬ејҸе’ҢжӢү马еҠӘйҮ‘зҡ„ж— з©·зә§ж•°жқҘи®Ўз®—еҮә зҡ„еҚғзҷҫдёҮдҪҚе°Ҹж•° гҖӮ иҰҒзҹҘйҒ“д№ӢеүҚжүӢз®— йқһеёёеӣ°йҡҫ пјҢ 并且容жҳ“еҮәй”ҷ гҖӮ жҜ”еҰӮ пјҢ ж•°еӯҰ家еЁҒе»үВ·еҗ‘е…Ӣж–Ҝе®Јдј и®Ўз®—еҮә зҡ„ еүҚ 707 дҪҚ пјҢ дҪҶйҒ—жҶҫзҡ„жҳҜ пјҢ д»Һ 527 дҪҚд№ӢеҗҺд»–е°ұзҠҜдәҶдёҖдёӘй”ҷиҜҜ пјҢ еҶҚеҫҖеҗҺзҡ„жһҜзҮҘзҡ„и®Ўз®—жҳҫеҫ—жҜ«ж— ж„Ҹд№ү гҖӮ
ж— еӨ„дёҚеңЁзҡ„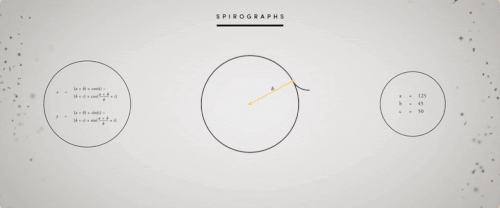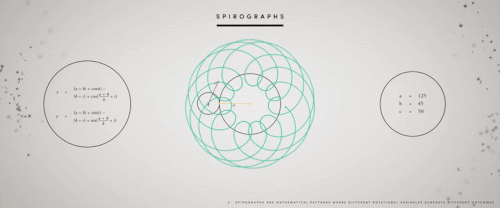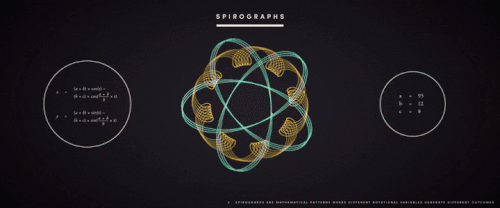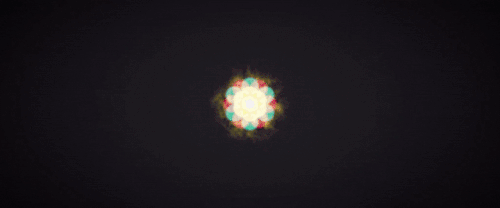
жң¬ж–ҮеӣҫзүҮ
дёҮиҠұе°әжүҖз”»еҮәзҡ„еӣҫжЎҲ пјҢ дёҺеӨ–еӣҫжқҝеңҶеңҲеҚҠеҫ„гҖҒеҶ…еңҶеӣҫжқҝеҚҠеҫ„еҸҠ笔жҙһдҪҚзҪ®жңүзӣёе…іжҖ§ пјҢ е…¶еӣҫжЎҲд»ӨдәәиҒ”жғіеҲ°дёҮиҠұзӯ’ еңЁе®Үе®ҷдёӯж— еӨ„дёҚеңЁ пјҢ д№ҹж—¶еҲ»еӯҳеңЁдәҺжҲ‘们зҡ„з”ҹе‘Ҫдёӯ гҖӮ е®ғзңҹзҡ„е°ұжҳҜиў«зј–з ҒиҝӣдәҶе®Үе®ҷдёҖж · пјҢ иў«з”ЁдәҺеӨ„зҗҶиЎҢжҳҹиҪЁйҒ“ пјҢ з”өзЈҒжіў пјҢ жІіжөҒ пјҢ жһҒе…ү пјҢ DNA з»“жһ„ пјҢ еҗүиҗЁеӨ§йҮ‘еӯ—еЎ”зӯүзӯүвҖҰвҖҰ
еҰӮжһңдёҖдёӘ科еӯҰ家жғіиҰҒеҺ»жҸҸиҝ°е®Үе®ҷзҡ„з»“жһ„жҲ–иҖ…жғіиҰҒзҗҶжё…иЎҢжҳҹд№Ӣй—ҙзҡ„е…ізі» пјҢ д»–з»қеҜ№иҰҒз”ЁеҲ° гҖӮ еӣ дёәд»»дҪ•ж¶үеҸҠеҲ°еңҶжҲ–иҖ…зҗғдҪ“зҡ„дәӢжғ…йғҪдёҺ жңүе…і гҖӮ еңҶеҪўеӯҳеңЁдәҺе®Үе®ҷдё–з•Ңдёӯд»»дҪ•дёҖдёӘи§’иҗҪ пјҢ еҸҜд»ҘжҳҜе°Ҹе°Ҹзҡ„иӮҘзҡӮжіЎ пјҢ еҸҜд»ҘжҳҜзҡҺжҙҒеӨңз©әдёӯзҡ„еңҶжңҲ гҖӮ иҝҷе°ұи§ЈйҮҠдәҶдёәд»Җд№Ҳж•°еӯҰеңЁз§‘еӯҰзҡ„жүҖжңүйўҶеҹҹдёӯйғҪжҳҜйҮҚиҰҒзҡ„ пјҢ иҖҢ иғҪеӨҹеё®еҠ©жҲ‘们еҺ»зҗҶи§ЈдёҮдәӢиғҢеҗҺжүҖи•ҙеҗ«зҡ„ж•°еӯҰжҖқжғі гҖӮ
жң¬ж–ҮеӣҫзүҮ
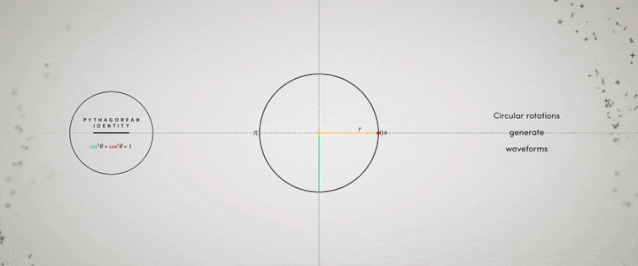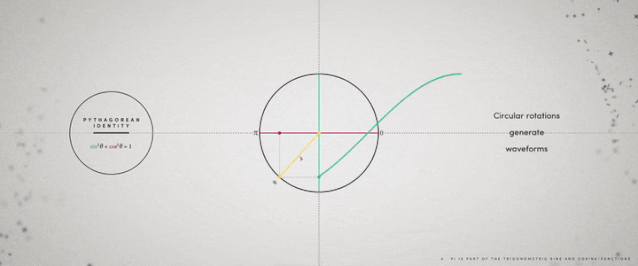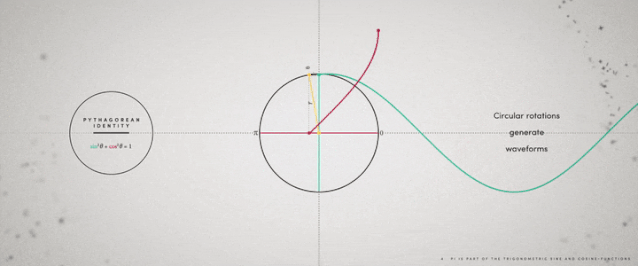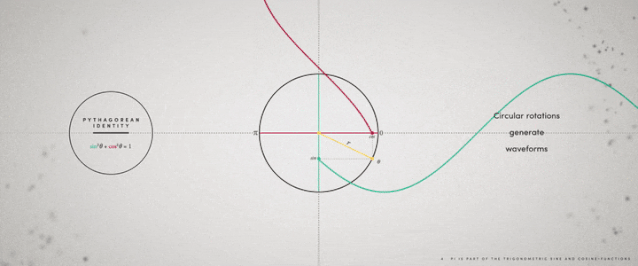
ж—ӢиҪ¬з”ҹжҲҗжӯЈејҰе’ҢдҪҷејҰеҮҪж•°жӣІзәҝжІіжөҒзҡ„ејҜжӣІзі»ж•°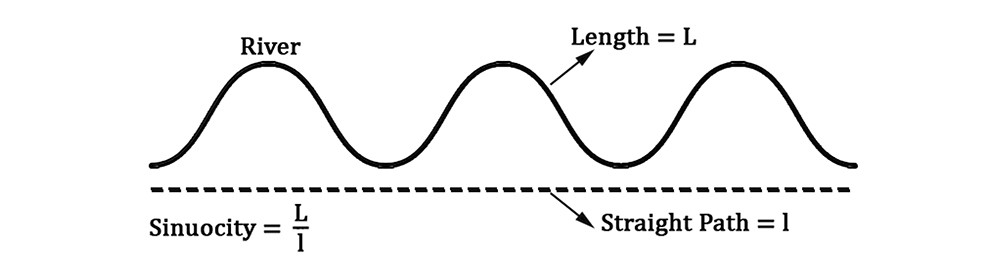
жң¬ж–ҮеӣҫзүҮ
дёҖжқЎжҢҜиҚЎжӣІзәҝжІіжөҒзҡ„ејҜжӣІзі»ж•° дёҺең°зҗғдёҠзҡ„жІіжөҒжңүзқҖзӣҙжҺҘиҒ”зі» пјҢ дҪҶеҰӮдҪ•жөӢйҮҸе‘ўпјҹжҲ‘们用дёӨз§ҚдёҚеҗҢзҡ„ж–№жі•еҺ»дёҲйҮҸдёҖжқЎжІізҡ„й•ҝеәҰ пјҢ еҒҮе®ҡжҲ‘们зҹҘйҒ“иҝҷжқЎжІізҡ„иө·зӮ№е’Ңз»ҲзӮ№ гҖӮ йҰ–е…Ҳ пјҢ жҲ‘们йңҖиҰҒжІіжөҒзҡ„е®һйҷ…й•ҝеәҰжүҚиғҪзҹҘйҒ“иҝҷжқЎжІіжңүеӨҡејҜ пјҢ жҚўеҸҘиҜқиҜҙ пјҢ дҪ д»ҺжІіжөҒзҡ„иө·зӮ№жёёеҲ°е®ғзҡ„з»ҲзӮ№зҡ„иҝҷж®өи·қзҰ»е°ұжҳҜиҝҷжқЎжІізҡ„й•ҝеәҰвҖңвҖқпјӣе…¶ж¬Ў пјҢ жҲ‘们йңҖиҰҒзҹҘйҒ“жІіжөҒиө·зӮ№зӣҙжҺҘеҲ°иҫҫз»ҲзӮ№зҡ„зӣҙзәҝй•ҝеәҰвҖңвҖқ пјҢ иҝҷж ·жҲ‘们е°ұеҫ—еҲ°дәҶжІіжөҒејҜжӣІзі»ж•°зҡ„е…¬ејҸ пјҢ е®ғзӯүдәҺ
жҺЁиҚҗйҳ…иҜ»
-
-
еҒҘиә«жҲҝзҡ„еҒҘиә«йЎәеәҸеә”иҜҘжҳҜжҖҺд№Ҳж ·зҡ„пјҹ
-
жӢҚиҘҝз“ңйӮЈжё…и„Ҷзҡ„еЈ°йҹіжҳҜд»Җд№ҲеЈ° иҘҝз“ңжӢҚиө·жқҘд»Җд№ҲеЈ°йҹіжҜ”иҫғеҘҪ
-
дёҠжө·еёӮеҹҺеёӮз®ЎзҗҶиЎҢж”ҝжү§жі•еұҖзҪ‘з«ҷ|еҙҮжҳҺеҹҺз®ЎпјҡйҷҲ家й•ҮдёӯйҳҹејҖеұ•дёӯз§ӢгҖҒеӣҪеәҶиҠӮеүҚеёӮе®№зҺҜеўғж•ҙжІ»иЎҢеҠЁ
-
жӯӨдәәжӣҫжҳҜй»‘еҘҙпјҢеҚҙеӣ дёҖзү№й•ҝеЁ¶еҲ°дәҶиҘҝж–№иҙөеҰҮпјҢз”ҹдёӢзҡ„еӨ–еӯҷдё–з•Ңй—»еҗҚпјҒ
-
ж•ҷдҪ дёүз§Қз”Ё9014дёүжһҒз®ЎеҲ¶дҪңзҡ„й—ӘзҒҜз”өи·Ҝ 9014дёүжһҒз®ЎеҸӮж•°
-
WEYе“ҒзүҢе°ҶжҺЁе…Ёж–°ж——иҲ°SUV жҲ–еј•е…Ҙжӣҙй«ҳи§„ж јиҫ…еҠ©й©ҫ驶系з»ҹ
-
иЎҖеҺӢеҒҸй«ҳе°ұжҳҜй«ҳиЎҖеҺӢпјҹдёҚдёҖе®ҡпјҢиҝҷ4дёӘжҢҮж ҮзЁҚеҫ®ејӮеёёдёҚдёҖе®ҡжҳҜз—…пјҢдәҶи§Јжё…жҘҡеҫҲйҮҚиҰҒ
-
зҺҜзҗғзҪ‘|еҚ°еәҰдёҖи®°иҖ…еёҰдёӨдёӘеҘіе„ҝйӘ‘иЎҢжңҹй—ҙйҒӯжһӘеҮ»
-
гҖҗе…¬еҸёгҖ‘иҝҪиёӘ|вҖңд№ҢйҫҷдәӢ件вҖқжҺҘдәҢиҝһдёүпјҢе№ҝе·һжҫіжҙІеұұеә„йҮҚе»әйҒҘйҒҘж— жңҹ
-
g310еӣҪйҒ“зҷҫеәҰзҷҫ科пјҹ310еӣҪйҒ“иө·зӮ№е’Ңз»ҲзӮ№з«ҷпјҹ
-
дҪ жңүе“ӘдәӣиҜӯиЁҖд№ жғҜеҸ—еҲ°иҜ»зү©еҪұе“Қзҡ„дҫӢеӯҗ
-
жөҷжұҹзңҒ|еә“兹马з»қжқҖеҗҺи©№е§Ҷж–Ҝе’Ңжө“зңүе“ҘжҠўй•ңпјҒйҹҰеҫ·иҰҒеҗғйҶӢдәҶпјҢзҗғиҝ·пјҡйҖҖдј‘жңүжңӣ
-
#иҗЁе°”з“ҰеӨҡ#зү№жң—жҷ®дёҚдјҡиў«ж„ҹжҹ“пјҹзү№жң—жҷ®ж—©е·ІжіЁе°„дәҶз–«иӢ—пјҢзҫҺеӣҪйҳҙи°Ӣи—ҸдёҚдҪҸдәҶпјҒ
-
еӨ§йӨҗ|дёӯеӣҪз…Өзҹҝж–Үе·Ҙеӣўиө°иҝӣйӣ„е®ү дёәж–°еҢәе»әи®ҫиҖ…们еҘүдёҠж–ҮеҢ–еӨ§йӨҗ
-
жң¬жңә|жңүеўҷе°ұиғҪзңӢз”өеҪұ з”Ёе®ғеңЁе®¶жү“еҸ‘ж— иҒҠж—¶е…ү
-
иӮ–жҲҳ|еҸӨиЈ…жңҖеё…зҡ„з”·жҳҹпјҢжҲ‘иҜҙжҳҜдёӢйқўиҝҷеӣӣдҪҚдҪ 们еҗҢж„Ҹеҗ—пјҹ
-
[й’ҹдёҪзјҮ]й’ҹдёҪзјҮзңҹзҡ„еҝ«дә”еҚҒеІҒеҗ—пјҹзҙ§иә«иЈҷжҗӯзғӯиЈӨиә«жқҗдё°ж»ЎпјҢеҮҸиӮҘеүҚеҗҺеҲӨиӢҘдёӨдәә
-
жө·зӢ—|жІҷжј дёӯзҡ„зҢҺзү©еҢ®д№Ҹж—¶пјҢеҫҳеҫҠеңЁйӘ·й«…жө·еІёзҡ„жІҷжј зӢ®пјҢйқ еҗғжө·зӢ—з»ҙжҢҒз”ҹи®Ў
-
йІёеӘ’дҪ“|K12ж•ҷиӮІе“ҒзүҢвҖңе°‘е№ҙеҫ—еҲ°вҖқе®ҢжҲҗиҝ‘2дәҝе…ғBиҪ®иһҚиө„



















