ж•°еӯҰ|йҡҗи—ҸеңЁ ПҖ дёӯзҡ„зҫҺдёҪ( дёғ )
жңҖйҮҚиҰҒзҡ„жҳҜд»ҺиҝҷдёӘе…¬ејҸйҮҢжҲ‘们зңӢеҮәжІіжөҒејҜжӣІзі»ж•°жІЎжңүдёҠйҷҗеҖј пјҢ дёҖжқЎжІід№ҹеҸҜд»ҘйқһеёёејҜ гҖӮ 然иҖҢ пјҢ ең°зҗғ科еӯҰ家 Hans-Henrik St?lum и®Ўз®—еҮәдәҶдё–з•Ңеҗ„ең°зҡ„жүҖжңүжІіжөҒејҜжӣІзі»ж•°зҡ„е№іеқҮеҖјжҳҜ 
жң¬ж–ҮеӣҫзүҮ
дёҖжқЎжІіжөҒиҮӘ1984иҮі2012зҡ„иңҝиң’еҸҳиҝҒе…ідәҺејҜжӣІзі»ж•°иҝҳжңүдёҖдёӘжңүи¶Јзҡ„дәӢе®һ пјҢ жІіжөҒеҸҜд»ҘеңЁжҹҗдәӣең°еҪўдҪңз”ЁдёӢдјҡеҸҳеҫ—йқһеёёејҜжӣІ пјҢ дҪҶеҶҚеҫҖеҗҺеҸҲзӘҒ然еҸҳзӣҙ пјҢ иҝҷж ·еңЁжҹҗдәӣиҢғеӣҙеҶ…е®ғзҡ„ејҜжӣІзі»ж•°еҖјдјҡеҫҲеӨ§ пјҢ дҪҶжҳҜжҖ»дҪ“жұӮе№іеқҮд№ӢеҗҺеҸҲиғҪзӯүдәҺ
еңЁеӨ§иҮӘ然дёӯеҜ»жүҫ
и’ҷзү№еҚЎзҪ—ж–№жі•и’ҷзү№еҚЎзҪ—ж–№жі•жҳҜдёҖз§Қд»ҘжҰӮзҺҮз»ҹи®ЎзҗҶи®әдёәжҢҮеҜјзҡ„ж•°еҖји®Ўз®—ж–№жі• гҖӮ е®ғз”ЁйҡҸжңәж•°пјҲжҲ–жӣҙеёёи§Ғзҡ„дјӘйҡҸжңәж•°пјүжқҘи§ЈеҶіеҫҲеӨҡи®Ўз®—й—®йўҳзҡ„ж–№жі• гҖӮ
зҺ°еңЁеҒҮе®ҡжҲ‘们жңүдёҖеј зҪ‘ж јеһӢеқҗж Үзәё пјҢ е»әз«ӢжңүеҺҹзӮ№зҡ„е№ійқўзӣҙи§’еқҗж Үзі» пјҢ еҲ©з”Ёд»ӢдәҺ 0 е’Ң 1 д№Ӣй—ҙзҡ„ж•°еҜ№ж ҮеҮәеқҗж Үе№ійқўдёҠ第дёҖиұЎйҷҗзҡ„зӮ№ пјҢ еңЁиҝҷиҝҮзЁӢдёӯ пјҢ дҪ дјҡеҸ‘зҺ°дёҖдәӣзӮ№еҲ°еҺҹзӮ№зҡ„и·қзҰ»е°ҸдәҺ 1 пјҢ дёҖдәӣзӮ№еҲ°еҺҹзӮ№зҡ„и·қзҰ»еӨ§дәҺ 1 пјҢ иҖҢиҝҷдәӣзӮ№д№Ӣй—ҙе°ұжҳҜеӣӣеҲҶд№ӢдёҖзҡ„еңҶе‘Ё пјҢ е®ғзҡ„йқўз§ҜеҮ д№Һе°ұжҳҜ 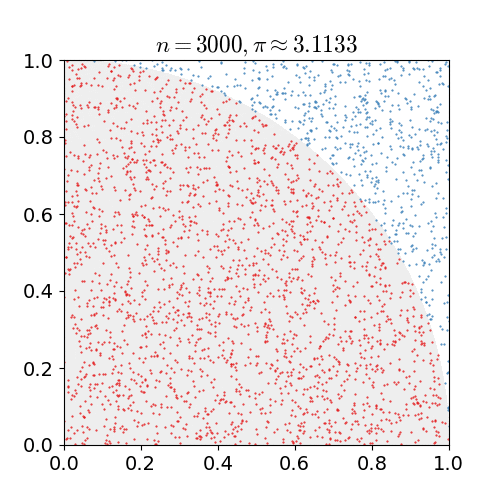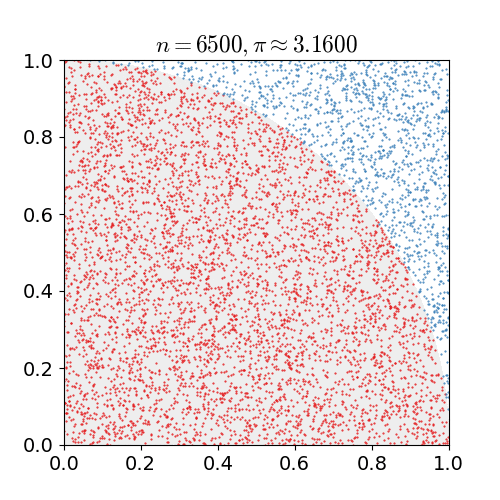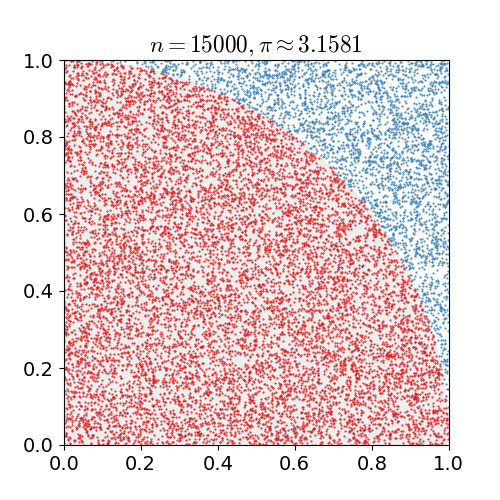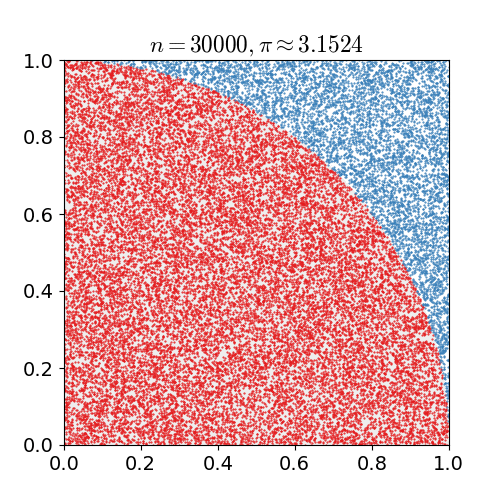
жң¬ж–ҮеӣҫзүҮ
дҪҝз”Ёи’ҷзү№еҚЎзҪ—ж–№жі•дј°з®—
иҝҷйҮҢи®ҫй’Ҳзҡ„й•ҝеәҰжҳҜ l пјҢ е№іиЎҢзәҝд№Ӣй—ҙзҡ„и·қзҰ»дёә
жҺЁиҚҗйҳ…иҜ»
- иҝҳзҸ ж јж ј |еҘ№жҳҜгҖҠиҝҳзҸ гҖӢдёӯзҡ„иҖҒдҪӣзҲ·пјҢе’ҢдёҲеӨ«з»“е©ҡ20еӨҡе№ҙд»ҚжҒ©зҲұеҰӮеҲқпјҢи®©дәәзҫЎж…•
- жҳҺжҳҹе©ҡ姻|зӣҳзӮ№еЁұд№җеңҲдёӯзҡ„е№ІдәІпјҢеҲҳеҫ·еҚҺз»ҷж”ҜжҢҒпјҢе‘Ёжҳҹй©°з»ҷеҗҚж°”пјҢиҖҢд»–д»ӨдәәдҪңе‘•пјҒ
- ж”ҫйЈһиҮӘжҲ‘|гҖҠд№җйҳҹзҡ„еӨҸеӨ©гҖӢе®Ңж»ЎиҗҪ幕пјҢиҝҷдёӘиөӣжһңи·ҹдҪ еҝғзӣ®дёӯзҡ„HOT5е·®еҲ«еӨ§еҗ—пјҹ
- е’ҢеҢҲеҘҙ|вҖңдҪҶдҪҝйҫҷеҹҺйЈһе°ҶеңЁвҖқдёӯзҡ„вҖңйҫҷеҹҺйЈһе°ҶвҖқпјҢеҲ°еә•жҢҮзҡ„и°Ғзӯ”жқҺе№ҝжҳҜй”ҷзҡ„
- з»јиүә|гҖҠжј”е‘ҳиҜ·е°ұдҪҚгҖӢдёӯзҡ„е•ҶдёҡејҸеҗ№жҚ§пјҢдёҖзңӢе°ұзҹҘйҒ“йғҪжҳҜиҖҒжҚ§е“ҸдәҶ
- ж·ұжө·еҠЁзү©|зғӯеёҰйӣЁжһ—дёӯзҡ„йёҹзұ»е’Ңж·ұжө·дёӯзҡ„и •иҷ«пјҢжҲ‘们иҜҘдҝқжҠӨе“ӘдёӘпјҹ
- еә§жӨ…|иө°иҝӣеҗҙиҺ«ж„ҒзҺ°е®һдёӯзҡ„家пјҢйӨҗеҺ…жҳҜиҰҒеҪ“дјҡи®®е®Өз”ЁпјҹдёӨжҺ’еә§жӨ…иғҪеқҗеҮ еҚҒдәә
- и®әж–Ү|2020еҚҺж•°д№Ӣжҳҹйқ’е°‘е№ҙж•°еӯҰеӨ§дјҡе®ҢзҫҺ收е®ҳ ж ёжЎғзј–зЁӢеӯҰе‘ҳж–©иҺ·е…ЁеӣҪеүҚдёү
- иӢұиҜӯ|жө·еә•е°ҸзәөйҳҹеӯҰиӢұиҜӯжҗәжүӢиұҢиұҶжҖқз»ҙ дёәз”ЁжҲ·жҸҗдҫӣиӢұиҜӯж•°еӯҰеҸҢ科еҗҜи’ҷ
- йғҪеҸҜд»Ҙ|жңүзҪ‘еҸӢжҸҗй—®вҖңзӣёдәІиҠӮзӣ®дёӯзҡ„еҘіеҳүе®ҫпјҢйғҪжҳҜд»Һе“ӘйҮҢиҜ·жқҘзҡ„пјҹвҖқзңҹзӣёеҺҹжқҘжҳҜиҝҷж ·зҡ„