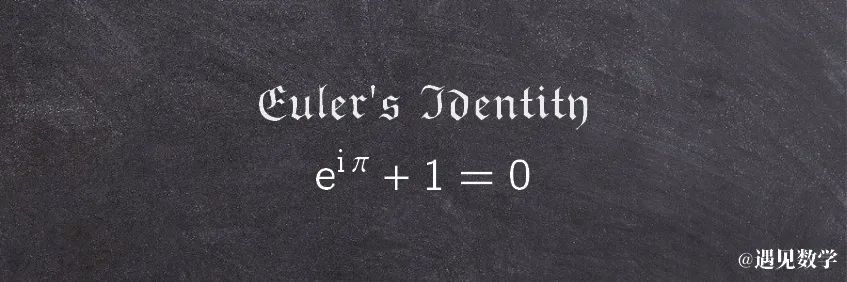(3.1408 and 3.1429 д№Ӣй—ҙ) гҖӮ еӣ жӯӨ пјҢ д»–и®Ўз®— еҲ°е°Ҹж•°зӮ№еҗҺзҡ„зІҫзЎ®дёӨдҪҚ гҖӮ йҳҝеҹәзұіеҫ·зҡ„жүӢеҠЁи®Ўз®—ж–№жі•еҪ“然иҝҳеҸҜд»ҘеҶҚж”№иҝӣ пјҢ иҝҷж ·д№ҹи®©д»–з©·е°ҪдёҖз”ҹйғҪжІЎжңүиҫҫжҲҗ гҖӮ
иҖҢжҲ‘еӣҪеҚ—еҢ—жңқеҲҳе®Ӣж—¶д»Јжқ°еҮәзҡ„ж•°еӯҰ家гҖҒеӨ©ж–ҮеӯҰ家зҘ–еҶІд№ӢеҲ©з”ЁеүІеңҶжңҜи®Ўз®— жӯЈ 24576 иҫ№еҪўзҡ„иҫ№й•ҝ пјҢ еҫ—еҲ° ПҖ вүҲ 355/113 пјҢ е…¶е°Ҹж•°зӮ№еҗҺзҡ„еүҚе…ӯдҪҚж•°йғҪжҳҜжӯЈзЎ®еҖј гҖӮ иҝҷж ·зҡ„з»“жһңеңЁд№ӢеҗҺзҡ„е…«зҷҫе№ҙеҶ… пјҢ йғҪжҳҜеҮҶзЎ®еәҰжңҖй«ҳзҡ„ дј°и®ЎеҖј гҖӮ
ж•°еӯҰ家们йңҖиҰҒеҺ»жүҫеҲ°жӣҙжңүж•Ҳзҡ„е…¬ејҸе’Ңжӣҙж–°зҡ„ж•°еӯҰж–№жі• гҖӮ еҫ®з§ҜеҲҶзҡ„еҸ‘жҳҺдҪҝеҫ— зҡ„и®Ўз®—жңүдәҶдёҖж¬ЎеӨ§зҡ„йЈһи·ғ гҖӮ д№ӢеҗҺ пјҢ ж•°еӯҰ家ејҖе§Ӣз”Ёж— з©·зә§ж•°зҡ„ж–№ејҸжқҘи®Ўз®— гҖӮ ж— з©·зә§ж•°жҳҜжңүеәҸзҡ„ж— з©·дёӘж•°еӯ—е’Ңзҡ„иЎЁиҫҫејҸ пјҢ иҖҢ且收ж•ӣзҡ„ж— з©·зә§ж•°дјҡеҫ—еҲ°дёҖдёӘзү№е®ҡзҡ„еҖј гҖӮ
еҪ“д»Ҡдё–з•Ңдәәзұ»жңүеҫҲеӨҡж–№жі•еҺ»и®Ўз®— пјҢ жңҖж—©зҡ„ж јйӣ·жһңйҮҢ-иҺұеёғе°јиҢЁе…¬ејҸеҰӮдёӢеӣҫжүҖзӨә гҖӮ иҝҷж ·еҲ©з”Ёж— з©·зә§ж•°еҺ»иЎЁзӨәеҸҚжӯЈеҲҮеҮҪж•° arctanx пјҢ жҠҠж— з©·еӨҡдёӘе°Ҹж•°еҠ еҲ°дёҖиө·и®Ўз®—еҮәдәҶ гҖӮ
>
еҪ“ x=1 д»Је…Ҙж–№зЁӢеҚіиғҪжұӮеҫ— /4 зҡ„еҖј гҖӮ дәә们жүҖеұ•ејҖзҡ„йЎ№и¶ҠеӨҡ пјҢ з»“жһңи¶Ҡи¶Ӣиҝ‘дәҺ гҖӮ дёҚиҝҮиҜҘзә§ж•°ж”¶ж•ӣйҖҹеәҰе®һеңЁеӨӘж…ў пјҢ дёәдәҶзІҫзЎ®еҫ—еҲ° е°Ҹж•°зӮ№еҗҺ 10 дҪҚ пјҢ жҲ‘们иҰҒжҠҠеӨ§зәҰ 50 дәҝйЎ№еҠ иө·жқҘжүҚеҘҪ гҖӮ
жҺўз©¶ зҡ„йҒ“и·ҜдёҠеҶҚеҫҖеҗҺеҸ‘еұ• пјҢ еҸҰдёҖдҪҚдјҹеӨ§зҡ„ж•°еӯҰ家欧жӢүпјҲLeonhard Eulerпјүзҷ»еңә гҖӮ еңЁд»– 28 еІҒ(1735е№ҙ)зҡ„ж—¶еҖҷдёәи§ЈеҶіеҪ“ж—¶йҡҫеҖ’欧жҙІжүҖжңүж•°еӯҰ家зҡ„дёҖдёӘйҡҫйўҳ пјҢ дёәеңҶе‘ЁзҺҮжүҫеҲ°дәҶдёӢйқўиҝҷдёӘжӣҙеҰҷдёҚеҸҜиЁҖзҡ„ж•°еӯҰиЎЁзӨәзӯүејҸ пјҢ 并且з”ұд»–ејҖе§ӢдҪҝз”ЁеёҢи…Ҡеӯ—жҜҚвҖңвҖқиЎЁзӨәеңҶе‘ЁзҺҮ гҖӮ д№ӢеҗҺиҝҷдёӘз¬ҰеҸ·иў«ж¬§жҙІж•°еӯҰ家жүҖжҺҘеҸ— пјҢ 并еә”з”ЁејҖжқҘ гҖӮ
>
дёҠйқўе…¶е®һе°ұжҳҜе·ҙеЎһе°”й—®йўҳзҡ„еҮҶзЎ®з»“жһң пјҢ иҝҷж ·е…¶е®һи®Ўз®—еҫ—д№ҹжҳҜж— з©·зә§ж•°е’Ң гҖӮ дёҚиҝҮ пјҢ зңҹжӯЈеҘҮеҰҷзҡ„жҳҜжүҖжңүе№іж–№ж•°еҖ’ж•°д№Ӣе’Ңеұ…然дёҺ жҗӯдёҠдәҶе…ізі» гҖӮ
йҷӨжӯӨд№ӢеӨ– пјҢ 欧жӢүиҝҳеңЁеҸҰдёҖдёӘжјӮдә®зҡ„ж–№зЁӢдёӯз”ЁеҲ° пјҢ еҚіж¬§жӢүжҒ’зӯүејҸ гҖӮ
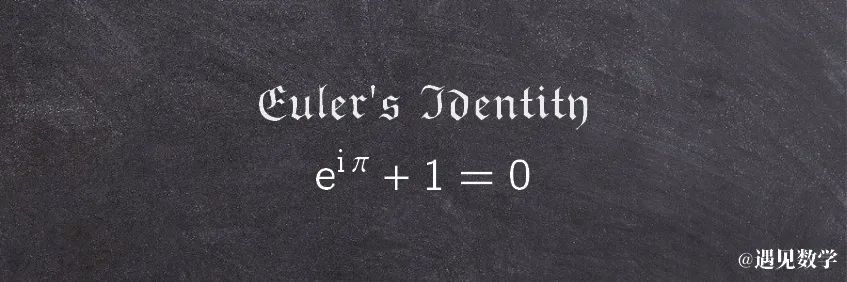
жң¬ж–ҮеӣҫзүҮ
и®Ўз®— зҡ„ж–№жі•еҶҚж”№иҝӣ пјҢ ж„ҹи°ўеҚ°еәҰж•°еӯҰ家ж–ҜйҮҢе°јз“Ұз‘ҹВ·жӢү马еҠӘйҮ‘з»ҷеҮәдәҶдёӢйқўж–°зҡ„и®Ўз®—
жҺЁиҚҗйҳ…иҜ»
-
-
еҒҘиә«жҲҝзҡ„еҒҘиә«йЎәеәҸеә”иҜҘжҳҜжҖҺд№Ҳж ·зҡ„пјҹ
-
жӢҚиҘҝз“ңйӮЈжё…и„Ҷзҡ„еЈ°йҹіжҳҜд»Җд№ҲеЈ° иҘҝз“ңжӢҚиө·жқҘд»Җд№ҲеЈ°йҹіжҜ”иҫғеҘҪ
-
дёҠжө·еёӮеҹҺеёӮз®ЎзҗҶиЎҢж”ҝжү§жі•еұҖзҪ‘з«ҷ|еҙҮжҳҺеҹҺз®ЎпјҡйҷҲ家й•ҮдёӯйҳҹејҖеұ•дёӯз§ӢгҖҒеӣҪеәҶиҠӮеүҚеёӮе®№зҺҜеўғж•ҙжІ»иЎҢеҠЁ
-
жӯӨдәәжӣҫжҳҜй»‘еҘҙпјҢеҚҙеӣ дёҖзү№й•ҝеЁ¶еҲ°дәҶиҘҝж–№иҙөеҰҮпјҢз”ҹдёӢзҡ„еӨ–еӯҷдё–з•Ңй—»еҗҚпјҒ
-
ж•ҷдҪ дёүз§Қз”Ё9014дёүжһҒз®ЎеҲ¶дҪңзҡ„й—ӘзҒҜз”өи·Ҝ 9014дёүжһҒз®ЎеҸӮж•°
-
WEYе“ҒзүҢе°ҶжҺЁе…Ёж–°ж——иҲ°SUV жҲ–еј•е…Ҙжӣҙй«ҳи§„ж јиҫ…еҠ©й©ҫ驶系з»ҹ
-
иЎҖеҺӢеҒҸй«ҳе°ұжҳҜй«ҳиЎҖеҺӢпјҹдёҚдёҖе®ҡпјҢиҝҷ4дёӘжҢҮж ҮзЁҚеҫ®ејӮеёёдёҚдёҖе®ҡжҳҜз—…пјҢдәҶи§Јжё…жҘҡеҫҲйҮҚиҰҒ
-
зҺҜзҗғзҪ‘|еҚ°еәҰдёҖи®°иҖ…еёҰдёӨдёӘеҘіе„ҝйӘ‘иЎҢжңҹй—ҙйҒӯжһӘеҮ»
-
гҖҗе…¬еҸёгҖ‘иҝҪиёӘ|вҖңд№ҢйҫҷдәӢ件вҖқжҺҘдәҢиҝһдёүпјҢе№ҝе·һжҫіжҙІеұұеә„йҮҚе»әйҒҘйҒҘж— жңҹ
-
g310еӣҪйҒ“зҷҫеәҰзҷҫ科пјҹ310еӣҪйҒ“иө·зӮ№е’Ңз»ҲзӮ№з«ҷпјҹ
-
дҪ жңүе“ӘдәӣиҜӯиЁҖд№ жғҜеҸ—еҲ°иҜ»зү©еҪұе“Қзҡ„дҫӢеӯҗ
-
жөҷжұҹзңҒ|еә“兹马з»қжқҖеҗҺи©№е§Ҷж–Ҝе’Ңжө“зңүе“ҘжҠўй•ңпјҒйҹҰеҫ·иҰҒеҗғйҶӢдәҶпјҢзҗғиҝ·пјҡйҖҖдј‘жңүжңӣ
-
#иҗЁе°”з“ҰеӨҡ#зү№жң—жҷ®дёҚдјҡиў«ж„ҹжҹ“пјҹзү№жң—жҷ®ж—©е·ІжіЁе°„дәҶз–«иӢ—пјҢзҫҺеӣҪйҳҙи°Ӣи—ҸдёҚдҪҸдәҶпјҒ
-
еӨ§йӨҗ|дёӯеӣҪз…Өзҹҝж–Үе·Ҙеӣўиө°иҝӣйӣ„е®ү дёәж–°еҢәе»әи®ҫиҖ…们еҘүдёҠж–ҮеҢ–еӨ§йӨҗ
-
жң¬жңә|жңүеўҷе°ұиғҪзңӢз”өеҪұ з”Ёе®ғеңЁе®¶жү“еҸ‘ж— иҒҠж—¶е…ү
-
иӮ–жҲҳ|еҸӨиЈ…жңҖеё…зҡ„з”·жҳҹпјҢжҲ‘иҜҙжҳҜдёӢйқўиҝҷеӣӣдҪҚдҪ 们еҗҢж„Ҹеҗ—пјҹ
-
[й’ҹдёҪзјҮ]й’ҹдёҪзјҮзңҹзҡ„еҝ«дә”еҚҒеІҒеҗ—пјҹзҙ§иә«иЈҷжҗӯзғӯиЈӨиә«жқҗдё°ж»ЎпјҢеҮҸиӮҘеүҚеҗҺеҲӨиӢҘдёӨдәә
-
жө·зӢ—|жІҷжј дёӯзҡ„зҢҺзү©еҢ®д№Ҹж—¶пјҢеҫҳеҫҠеңЁйӘ·й«…жө·еІёзҡ„жІҷжј зӢ®пјҢйқ еҗғжө·зӢ—з»ҙжҢҒз”ҹи®Ў
-
йІёеӘ’дҪ“|K12ж•ҷиӮІе“ҒзүҢвҖңе°‘е№ҙеҫ—еҲ°вҖқе®ҢжҲҗиҝ‘2дәҝе…ғBиҪ®иһҚиө„