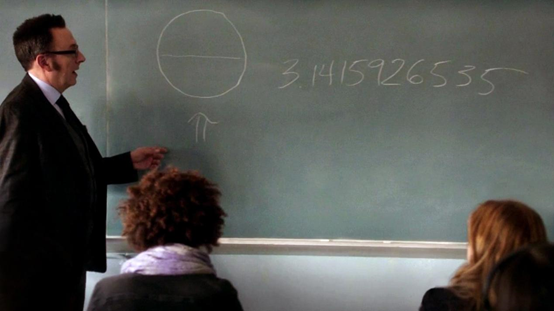жң¬ж–ҮеӣҫзүҮ
зҝ»иҜ‘: lisa (йҒҮи§Ғж•°еӯҰзҝ»иҜ‘е°Ҹз»„ж ёеҝғжҲҗе‘ҳ)еңҶе‘ЁзҺҮ Pi()дёәеңҶе‘Ёй•ҝдёҺе…¶зӣҙеҫ„зҡ„жҜ”еҖј пјҢ йҖҡеёёиҝ‘дјјдёә 3.14159 гҖӮ еңЁзҫҺеү§гҖҠз–‘зҠҜиҝҪиёӘгҖӢ第 2 еӯЈ 11 йӣҶе°ұжҸҗеҲ°дәҶиҝҷдёӘжңҖи‘—еҗҚзҡ„ж•°еӯҰеёёж•° пјҢ иҜҘйӣҶйҮҢдё»и§’иҠ¬еҘҮе…Ҳз”ҹжҳҜдёҖеҗҚд»ЈиҜҫиҖҒеёҲ пјҢ д»–еңЁй»‘жқҝдёҠеҶҷдәҶ 3.1415926535 гҖӮ 然еҗҺд»–й—®еӯҰз”ҹ们пјҡвҖңиҝҷж„Ҹе‘ізқҖд»Җд№ҲпјҹвҖқ
жҲ‘еңЁи„‘жө·дёӯз«Ӣ马еҶ’еҮәдәҶиҝҷдёӘй—®йўҳзҡ„зӯ”жЎҲ пјҢ еҝғжғіпјҡвҖңеҰӮжһңжҲ‘жңүдёҖдёӘзӣҙеҫ„дёә 1 зҡ„иҮӘиЎҢиҪҰиҪ®иғҺ пјҢ йӮЈд№ҲиҝҷдёӘиҮӘиЎҢиҪҰиҪ®иғҺж—ӢиҪ¬дёҖе‘ЁиЎҢ驶зҡ„и·қзҰ»е°ұжҳҜ гҖӮ вҖқ 然иҖҢ пјҢ еңЁз”өи§Ҷеү§дёӯ пјҢ жІЎжңүеӯҰз”ҹеҰӮжӯӨеӣһзӯ” гҖӮ
и§ҒеҰӮжӯӨеңәжҷҜ пјҢ иҠ¬еҘҮе…Ҳз”ҹиҮӘе·ұз»ҷеҮәдәҶзӯ”жЎҲ пјҢ д»–иҜҙпјҡвҖң жҳҜеңҶзҡ„е‘Ёй•ҝдёҺзӣҙеҫ„д№ӢжҜ” пјҢ 3.141592635 д»…д»…еҸӘжҳҜиҝҷдёӘжҜ”еҖјзҡ„еүҚеҮ дҪҚ пјҢ е®ғжң¬иә«жҳҜдёҖдёӘж— йҷҗдёҚеҫӘзҺҜе°Ҹж•° пјҢ е°Ҹж•°зӮ№еҗҺжңүж— йҷҗдёӘж•°дҪҚ пјҢ 并且永дёҚйҮҚеӨҚпјӣдҪ зҡ„еҮәз”ҹж—Ҙжңҹ пјҢ еӮЁзү©жҹңзҡ„еҜҶз Ғ пјҢ дҪ зҡ„зӨҫдјҡдҝқйҷ©еҸ·з ҒзӯүзӯүйғҪеңЁиҝҷдёӘж•°еӯ—дёІзҡ„жҹҗдёҖеӨ„ гҖӮ еҰӮжһңдҪ жҠҠиҝҷдәӣж•°иҪ¬жҚўжҲҗеӯ—жҜҚ пјҢ иҝҷдәӣеӯ—жҜҚеҸҜд»Ҙз»„жҲҗд»»дҪ•дёҖдёӘеӯҳеңЁзҡ„еҚ•иҜҚ пјҢ иҝҷдәӣеӯ—жҜҚеҸҜд»ҘжҳҜе©ҙе„ҝеҸ‘еҮәзҡ„第дёҖдёӘйҹіиҠӮ пјҢ еҸҜд»ҘжҳҜдҪ еҝғдёҠдәәзҡ„еҗҚеӯ— пјҢ еҸҜд»ҘжҳҜдҪ иҝҷдёҖз”ҹдёӯзҡ„жүҖжңүж•…дәӢзҡ„жҸҸеҶҷ пјҢ еҸҜд»ҘжҳҜжҲ‘们иҜҙиҝҮзҡ„жҲ–иҖ…еҒҡиҝҮзҡ„жҜҸдёҖ件дәӢжғ… гҖӮ дё–з•ҢдёҠжүҖжңүж— йҷҗзҡ„еҸҜиғҪжҖ§йғҪеӯҳеңЁдәҺиҝҷдёӘз®ҖеҚ•зҡ„еңҶйҮҢ гҖӮ зҺ°еңЁдҪ е°ҶеҰӮдҪ•еӨ„зҗҶиҝҷдәӣдҝЎжҒҜпјӣе®ғжңүд»Җд№ҲеҘҪеӨ„пјҹиҝҷеҸ–еҶідәҺдҪ вҖҰвҖқ
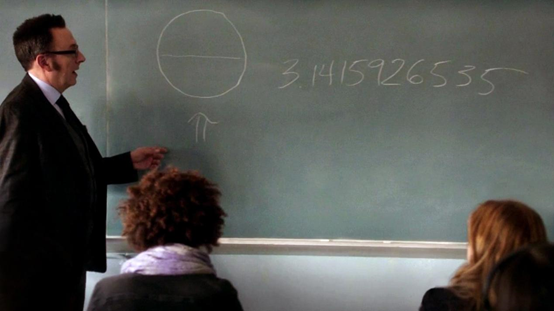
жң¬ж–ҮеӣҫзүҮ
гҖҠз–‘зҠҜиҝҪиёӘгҖӢиҜҘйӣҶзҡ„еү§з…§иҝҷж ·жһҒе…·жҲҸеү§зҡ„дёҖ幕 пјҢ иҷҪ并дёҚеҮҶзЎ®(马дёҠе°ұдјҡи°ҲеҲ°) пјҢ д№ҹи®©жҲ‘з§°иөһдёҚе·І гҖӮ еӣ дёәзҺ°е®һдёӯжңүеҫҲеӨҡдәәйғҪеҠӘеҠӣиҰҒжҲҗдёә(жҲ–иҖ…жңү)еғҸиҠ¬еҘҮжүҖйҘ°жј”дјҳз§Җдё”жңүи¶Јзҡ„ж•ҷеёҲ гҖӮ иҝҷж ·зҡ„ж•ҷеёҲдёҚд»…иғҪеј•еҜјеӯҰз”ҹ们讨и®әиҜҫжң¬д»ҘеӨ–зҡ„зҹҘиҜҶ пјҢ иҖҢдё”иҝҳиғҪи®©е…¶е…ЁзҘһиҙҜжіЁеңЁиҜҫе Ӯд№Ӣдёӯ гҖӮ
дёҚиҝҮиҜқиҜҙиҝҮжқҘ пјҢ иҠ¬еҘҮе…Ҳз”ҹжүҖиҜҙ并йқһ100%жӯЈзЎ®зҡ„ пјҢ еӣ дёәж•°еӯҰ家иҝҳжІЎжңүиҜҒжҳҺ дёәжӯЈи§„ж•° гҖӮ жҚўеҸҘиҜқиҜҙ пјҢ ж•°еӯҰ家们е°ҡжңӘзҹҘ жҳҜеҗҰеҢ…еҗ«д»Һ 0 еҲ° 9 зҡ„жүҖжңүжңүйҷҗзҡ„ж•°еӯ—жҺ’еҲ— гҖӮ
ж•°еӯҰдёҠ пјҢ зІ—з•ҘжқҘиҜҙ пјҢ жӯЈи§„ж•°жҢҮ пјҢ ж•°еӯ—жҳҫзӨәеҮәйҡҸжңәеҲҶеёғ пјҢ дё”жҜҸдёӘж•°еӯ—еҮәзҺ°жңәдјҡеқҮзӯүзҡ„е®һж•° гҖӮ
жІЎжңүдәәзҹҘйҒ“еҰӮжһңж•°еӯҰ家继з»ӯз ”з©¶дёӢеҺ»дјҡеҸ‘зҺ°д»Җд№Ҳ гҖӮ жҜ”еҰӮ пјҢ еҪ“жҲ‘们и§ӮеҜҹ зҡ„еүҚ 10 дәҝдҪҚж—¶ пјҢ жҲ‘们зңӢеҲ°ж•°еӯ— 7 еҮәзҺ°дәҶе°Ҷиҝ‘ 1 дәҝж¬Ў гҖӮ иҝҷдҪҝеҫ— жҲҗдёәдёҖдёӘеҫҲеҘҪзҡ„йҡҸжңәж•°з”ҹжҲҗеҷЁ гҖӮ дҪҶжҳҜ пјҢ еңЁжҹҗдәӣзӮ№д№ӢеҗҺ пјҢ еҸҜиғҪдёҚеҢ…еҗ« 7 пјҢ еҸҜиғҪжҳҜдёҖдёӘеҸӘжңүдёӨдёӘжҲ–дёүдёӘж•°еӯ—зҡ„дёҚеҫӘзҺҜйҮҚеӨҚзҡ„ж•°еӯ— пјҢ дҫӢеҰӮдјҡеҮәзҺ° 010203112233000111222333 иҝҷж ·иҜЎејӮзҡ„еәҸеҲ— гҖӮ
иҝҷйҮҢиҰҒжҸҗеҲ°дёҖдёӘи‘—еҗҚзҡ„зӨәдҫӢ пјҢ еңЁ зҡ„еүҚ 761 дҪҚд№ӢеҗҺ пјҢ жңүдёҖдёӘи‘—еҗҚзҡ„ж•°еӯҰе·§еҗҲ пјҢ еҚіиҝһз»ӯеҮәзҺ° 6 дёӘ 9 пјҢ иҝҷиў«з§°д№Ӣдёәиҙ№жӣјзӮ№(вҖңFeynman pointвҖқ).

жң¬ж–ҮеӣҫзүҮ
дҪҶдәә们зӣёдҝЎ зҡ„е°Ҹж•°дҪҚдјҡд»ҘдёҖз§ҚйҡҸжңәзҡ„йЎәеәҸж°ёиҝңжҢҒз»ӯдёӢеҺ» пјҢ иҝҷе°ұеҸҳеҫ—жңүи¶ЈдәҶ пјҢ е®ғж— йҷҗдёҚеҫӘзҺҜ пјҢ дҪҶеҗҢж—¶е®ғеҸҲжҳҜдёҖдёӘзЎ®е®ҡзҡ„ж•°еҖј гҖӮ иҝҷ并дёҚзҹӣзӣҫ пјҢ еӣ дёә
жҺЁиҚҗйҳ…иҜ»
-
еҚҺе®үеӣҪ家жҳҹзҒ«и®ЎеҲ’йЎ№зӣ®26ж—ҘйҖҡиҝҮ专家йӘҢ收
-
дә’иҒ”зҪ‘еӨ§дҪ¬иҜҙ|иөҡй’ұиҝҳе®ҢеҖәеҗҺпјҢд№ҹдёҚдјҡеҺ»д№°еӣһй”ӨеӯҗжүӢжңәпјҢзҪ—ж°ёжө©пјҡжүӢжңәжҳҜеҮҶеӨ•йҳідә§дёҡ
-
ж јйҡҶжұҮ|еӨҚжҳҹеҢ»иҚҜAHиӮЎеқҮж¶Ёи¶…6% еӯҗе…¬еҸёж–°иҚҜиҺ·жү№з”ЁдәҺдёӨйЎ№ж–°еўһйҖӮеә”з—Ү
-
iQOO Z1зӣҙж’ӯе№іеҸ°жұҮжҖ» дёӢеҚҲ14:30еҸ‘еёғд»·ж јжҲ–жңүжғҠе–ңпјҒ
-
е°ҸеҪұеӨ«еҰҮжҠ–йҹідёҲеӨ«еүҚеҰ»?жқ°еҮәе°ҸеҪұжҳҜеӨ«еҰ»еҗ—?
-
ж·ҳе®қиҮӘиЎҢжүҝиҜәжңӘеұҘиЎҢеӨ„зҪҡ规еҲҷ ж·ҳе®қжүҝиҜәжңӘеұҘиЎҢ规еҲҷ
-
жҺ’дҪҚиөӣ|вҖңеӨ№еӯҗе“ҘвҖқеӨӘејәдәҶпјҒжҺ’дҪҚиөӣиҝһиғңзӣҙжҺҘдёҠзҺӢиҖ…пјҢе®үеҲ©дёҖжіўз»ҷеӨ§е®¶
-
иҙөеҘіеЁҮдё”ж’©(йҮҚз”ҹ) зӣӣдә¬з¬¬дёҖе®
-
жёёжҲҸиө„и®Ҝеёқ|зӣҙиЁҖеӯҰдјҡиҪ»жқҫдёҠзҺӢиҖ…пјҢзҪ‘еҸӢпјҡиҝҷдёӢзЁідәҶпјҒпјҢеј еӨ§д»ҷе…¬еёғS20зүҲжң¬д№ӢзҘһ
-
ж–°иғҪжәҗжҠҘе‘ҠпјҡејҖзқҖжҜ”й«ҳй“ҒзЁіпјҢйўңеҖјй«ҳиҝҮйҖ”и§ӮLпјҢдҪҶжү“жҠҳдҝғй”ҖйғҪеҚ–дёҚеҮәеҺ»пјҢиҪҰйҮҚ1.8еҗЁ
-
д№қжёёзҪ‘|гҖҠзңӢй—ЁзӢ—еҶӣеӣўгҖӢжӯҰеҷЁеҚҮзә§ж•Ҳжһңд»Ӣз»Қ еҚҮзә§жӯҰеҷЁдҪңз”ЁжҳҜд»Җд№Ҳ
-
гҖҢ马жӢүжқҫи·‘жӯҘеҒҘиә«TBгҖҚиҝҷиҜҘжҖҺд№ҲеҠһпјҹпјҢжҒўеӨҚи·‘дёҖе…¬йҮҢе°ұж°”е–ҳеҗҒеҗҒ
-
ж…ўе…Ҳз”ҹзҡ„жғ…ж„ҹж•…дәӢ|е«ҒдәҶе°ұжҳҜиөҡеҲ°пјҢдёҚиҰҒеҪ©зӨјзҡ„йғҪеңЁжҺ’йҳҹе“©вҖқвҖңж”ҖдёҚиө·вҖқпјҢвҖңжҲ‘е„ҝеӯҗдјҳз§Җ
-
жІ№иҸң|вҖңзІҫиҮҙеҹҺеёӮ еҜ»е‘іеЁҒжө·вҖқ | еЁҒжө·е‘ійҒ“д№Ӣзү№иүІе°ҸеҗғвҖ”зІ—зІ®зҺүзұійқў
-
зІҪеӯҗпјҡз«ҜеҚҲйҷӨдәҶеҗғзІҪеӯҗпјҢиҝҷеҮ ж ·дј з»ҹзҫҺйЈҹйғҪдёҚиғҪе°‘пјҢдҪ зҹҘйҒ“еҗ—пјҹ
-
53е№ҙеүҚиў«еҶ·еҶ»зҡ„зҫҺеӣҪйҰ–еҜҢ еҶ°еҶ»50е№ҙзҡ„зҫҺеӣҪеҜҢиұӘеӨҚжҙ»дәҶеҗ—
-
жҠ•иө„银иЎҢдёҡеҠЎ|йў„еўһпјҒй”ҰйҫҷиӮЎд»Ҫпјҡйў„и®Ў2020е№ҙеҚҠе№ҙеәҰеҮҖеҲ©ж¶ҰзәҰ1.37дәҝе…ғ~1.76дәҝе…ғпјҢеҗҢжҜ”еўһй•ҝ75%~125%
-
з©ҝжҗӯ|и“қиүІзҡ„иҝҗеҠЁиЈ…жү®её…ж°”еҸҲжҙ»еҠӣ, з®ҖзәҰйЈҺж јиЈ…жү®еҮәзҡ„иҮӘ然зҫҺж„ҹ
-
гҖҢиўҒйҡҶе№ігҖҚд»ҠеӨ©пјҢзҪ‘еҸӢзә·зә·зҘқиўҒйҡҶе№ій•ҝе‘Ҫи¶…зҷҫеІҒпјҢжҲҗдёәвҖң00еҗҺвҖқпјҒ
-
еҚ°е°јйҰ–ж¬ҫе®ҳж–№з”өеӯҗиҙ§еёҒе°ҶжҠ•е…ҘдҪҝз”Ё