жҳҜеңҶзҡ„е‘Ёй•ҝе’Ңзӣҙеҫ„зҡ„жҜ”еҖј пјҢ жүҖд»Ҙе®ғжҳҜдёҖдёӘжңүзЎ®е®ҡеҖјзҡ„ж•°еӯҰеёёж•° гҖӮ еҪ“然 пјҢ йҖҡеёёзҡ„и®Ўз®—дёӯ пјҢ жҲ‘们еҸӘйңҖиҰҒ зҡ„иҝ‘дјјеҖје°ұеӨҹдәҶ гҖӮ
еңЁ 1768 е№ҙ пјҢ з‘һеЈ«ж•°еӯҰ家зәҰзҝ°В·жө·еӣ йҮҢеёҢВ·жң—дјҜиҜҒжҳҺдәҶ зҡ„еҖјжҳҜж— зҗҶж•° пјҢ жүҖд»Ҙе®ғдёҚиғҪеҶҷжҲҗеҲҶж•°зҡ„йӮЈж ·еҪўејҸ гҖӮ еңЁйӮЈд№ӢеүҚ 22/7 е°ұз»Ҹеёёиў«з”ЁжқҘеҪ“дҪң зҡ„иҝ‘дјјеҖј пјҢ иҷҪ然е®ғе®һйҷ…дёҠ并дёҚзӯүдәҺ гҖӮ жҲ‘们йғҪзҹҘйҒ“ж— зҗҶж•°дёҚиғҪеҶҷжҲҗдёӨдёӘж•ҙж•°зҡ„жҜ”еҖјпјҲеҚіеҲҶж•° пјҢ еғҸ a/b зҡ„еҪўејҸпјү пјҢ еӣ дёәж— зҗҶж•°жҳҜж— йҷҗзҡ„ пјҢ дё”дёҚеҫӘзҺҜзҡ„е°Ҹж•° гҖӮ
еҶҚеҗҺжқҘ 1882 е№ҙ пјҢ еҫ·еӣҪж•°еӯҰ家иҙ№иҝӘеҚ—еҫ·В·еҶҜВ·жһ—еҫ·жӣјиҜҒжҳҺдәҶ жҳҜдёҖдёӘи¶…и¶Ҡж•° пјҢ еҚідёҚжҳҜд»»ж„Ҹж•ҙзі»ж•°д»Јж•°еӨҡйЎ№ејҸзҡ„ж № гҖӮ
ж•°еӯҰ家йҮ‘з”°еә·жӯЈпјҲYasumasa KanadaпјүеҸ‘зҺ°еңҶе‘ЁзҺҮзҡ„еүҚдёҮдәҝдёӘж•°еӯ—еңЁз»ҹи®ЎеӯҰдёҠжҳҜйҡҸжңәзҡ„ гҖӮ еҰӮжһңдҪ жҹҘзңӢдёӢиЎЁ пјҢ дҪ дјҡеҸ‘зҺ°жҜҸдёӘж•°еӯ—еҸ‘з”ҹзҡ„дәӢ件жҳҜзӢ¬з«Ӣзҡ„ пјҢ еҸ‘з”ҹзҡ„жҰӮзҺҮзәҰжҳҜеҚҒеҲҶд№ӢдёҖ гҖӮ
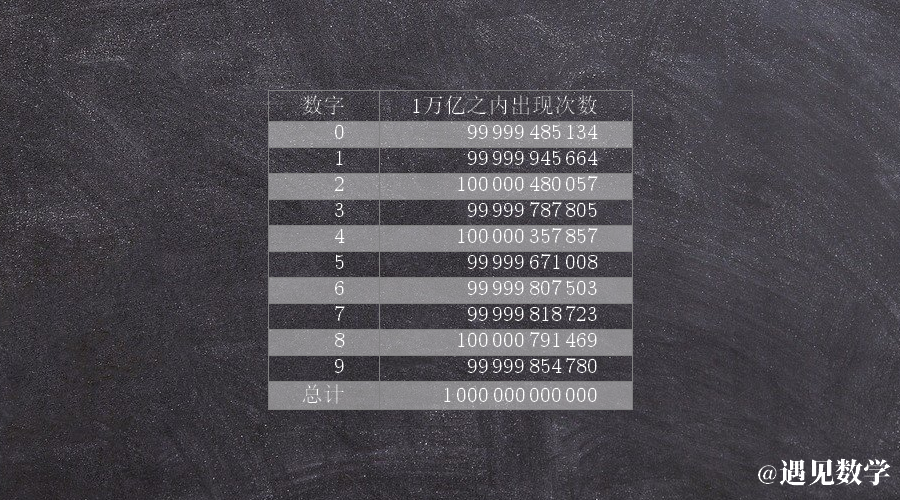
жң¬ж–ҮеӣҫзүҮ
еңҶе‘ЁзҺҮдёӯиҝһз»ӯзҡ„е…ӯдёӘ9и®ёеӨҡе№ҙд№ӢеҗҺзҡ„ 2019 е№ҙ пјҢ и°·жӯҢеҘіе·ҘзЁӢеёҲ Emma Haruko Iwao еҲ©з”Ёдә‘и®Ўз®—иө„жәҗ пјҢ иҠұдәҶ 121 еӨ©и®Ўз®—еҮә зҡ„ 34.1 дёҮдәҝдҪҚ гҖӮ дҪ еҸҜд»ҘеңЁдҪ и„‘жө·дёӯжғіиұЎиҝҷж ·зҡ„з”»йқўпјҡеҰӮжһңиҰҒз”Ёжҷ®йҖҡеӯ—дҪ“жү“еҚ° е°Ҹж•°зӮ№еҗҺзҡ„ 10 дәҝдҪҚ пјҢ е®ғзҡ„й•ҝеәҰе°Ҷд»ҺзҫҺеӣҪзәҪзәҰ延伸еҲ°е ӘиҗЁж–Ҝе·һпјҒ
然иҖҢ пјҢ 34.1 дёҮдәҝдҪҚиҝҷд№Ҳе·ЁеӨ§зҡ„ж•°еӯ—д»Қ然дёҚи¶ід»ҘеңЁж•°еӯҰдёҠиҜҒжҳҺ жҳҜжӯЈи§„ж•°жҲҗз«Ӣ гҖӮ и¶…зә§и®Ўз®—жңәд»ҚеңЁе°қиҜ•жҢ‘жҲҳи®Ўз®—жӣҙзІҫзЎ®зҡ„ гҖӮ дҪ жҹҘзңӢдёӢйқўзҡ„еӣҫиЎЁе°ұдјҡзңӢеҲ°иҮӘе…¬е…ғеүҚ 250 е№ҙд»ҘжқҘ пјҢ еҺҶеҸІж—¶й—ҙиҪҙеӣҫдёҠжҺўзҙўеңҶе‘ЁзҺҮзҡ„е·ІзҹҘдҪҚж•° гҖӮ
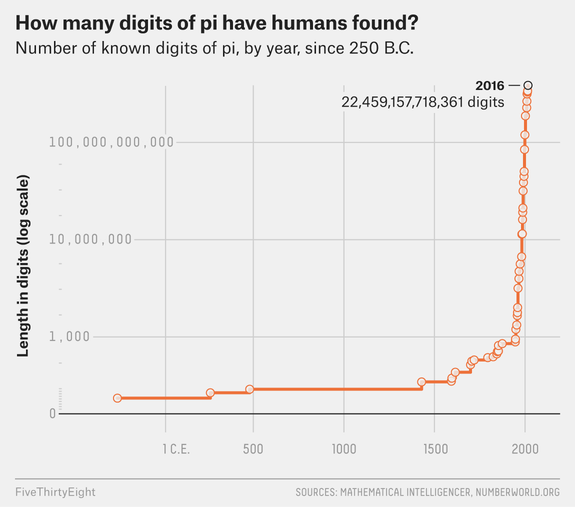
жң¬ж–ҮеӣҫзүҮ
еҪ“ж•°еӯҰ家еҸ‘зҺ°ж–°зҡ„з®—жі•гҖҒз”өи„‘еҸҳеҫ—жҷ®еҸҠж—¶ пјҢ зҡ„е·ІзҹҘе°Ҹж•°дҪҚе‘ҲжҢҮж•°еўһеҠ гҖӮ жіЁж„ҸеһӮзӣҙеқҗж ҮдҪҝз”ЁдәҶеҜ№ж•°еқҗж ҮеҶҚеӣһеҲ°ж–Үз« жҸҗеҲ°иҝҷйғЁзҫҺеү§дёӯиҠ¬еҘҮе…Ҳз”ҹ пјҢ жҲ‘们жҳҺзҷҪд»–жүҖиҜҙзҡ„д№ҹйқһй”ҷиҜҜ гҖӮ дҪ еҸҜд»ҘеҫҲиҪ»жқҫең°еңЁ дёӯжүҫеҲ°иҮӘе·ұзҡ„з”ҹж—Ҙ гҖӮ еҰӮжһңдҪ зҷ»йҷҶиҝҷдёӘзҪ‘еқҖ mypiday.com иҫ“е…ҘдҪ зҡ„з”ҹж—Ҙ пјҢ дёҠйқўе°ұдјҡжҳҫзӨәе®ғеңЁ дёӯзҡ„дҪҚзҪ® гҖӮ
еҰӮжһң жҳҜдёҖдёӘжӯЈи§„ж•° пјҢ йӮЈеҸҜд»ҘиҜҙжҲ‘们зҡ„ж•ҙдёӘе‘ҪиҝҗйғҪжҳҜз”Ё зј–з Ғ пјҢ е°ҶжқҘеҸ‘з”ҹзҡ„дёҖеҲҮз”»йқўпјҲеӣҫзүҮжҳҜдәҢиҝӣеҲ¶ж–Ү件пјүйғҪе°ҶеңЁ
жҺЁиҚҗйҳ…иҜ»
-
-
еҒҘиә«жҲҝзҡ„еҒҘиә«йЎәеәҸеә”иҜҘжҳҜжҖҺд№Ҳж ·зҡ„пјҹ
-
жӢҚиҘҝз“ңйӮЈжё…и„Ҷзҡ„еЈ°йҹіжҳҜд»Җд№ҲеЈ° иҘҝз“ңжӢҚиө·жқҘд»Җд№ҲеЈ°йҹіжҜ”иҫғеҘҪ
-
дёҠжө·еёӮеҹҺеёӮз®ЎзҗҶиЎҢж”ҝжү§жі•еұҖзҪ‘з«ҷ|еҙҮжҳҺеҹҺз®ЎпјҡйҷҲ家й•ҮдёӯйҳҹејҖеұ•дёӯз§ӢгҖҒеӣҪеәҶиҠӮеүҚеёӮе®№зҺҜеўғж•ҙжІ»иЎҢеҠЁ
-
жӯӨдәәжӣҫжҳҜй»‘еҘҙпјҢеҚҙеӣ дёҖзү№й•ҝеЁ¶еҲ°дәҶиҘҝж–№иҙөеҰҮпјҢз”ҹдёӢзҡ„еӨ–еӯҷдё–з•Ңй—»еҗҚпјҒ
-
ж•ҷдҪ дёүз§Қз”Ё9014дёүжһҒз®ЎеҲ¶дҪңзҡ„й—ӘзҒҜз”өи·Ҝ 9014дёүжһҒз®ЎеҸӮж•°
-
WEYе“ҒзүҢе°ҶжҺЁе…Ёж–°ж——иҲ°SUV жҲ–еј•е…Ҙжӣҙй«ҳи§„ж јиҫ…еҠ©й©ҫ驶系з»ҹ
-
иЎҖеҺӢеҒҸй«ҳе°ұжҳҜй«ҳиЎҖеҺӢпјҹдёҚдёҖе®ҡпјҢиҝҷ4дёӘжҢҮж ҮзЁҚеҫ®ејӮеёёдёҚдёҖе®ҡжҳҜз—…пјҢдәҶи§Јжё…жҘҡеҫҲйҮҚиҰҒ
-
зҺҜзҗғзҪ‘|еҚ°еәҰдёҖи®°иҖ…еёҰдёӨдёӘеҘіе„ҝйӘ‘иЎҢжңҹй—ҙйҒӯжһӘеҮ»
-
гҖҗе…¬еҸёгҖ‘иҝҪиёӘ|вҖңд№ҢйҫҷдәӢ件вҖқжҺҘдәҢиҝһдёүпјҢе№ҝе·һжҫіжҙІеұұеә„йҮҚе»әйҒҘйҒҘж— жңҹ
-
g310еӣҪйҒ“зҷҫеәҰзҷҫ科пјҹ310еӣҪйҒ“иө·зӮ№е’Ңз»ҲзӮ№з«ҷпјҹ
-
дҪ жңүе“ӘдәӣиҜӯиЁҖд№ жғҜеҸ—еҲ°иҜ»зү©еҪұе“Қзҡ„дҫӢеӯҗ
-
жөҷжұҹзңҒ|еә“兹马з»қжқҖеҗҺи©№е§Ҷж–Ҝе’Ңжө“зңүе“ҘжҠўй•ңпјҒйҹҰеҫ·иҰҒеҗғйҶӢдәҶпјҢзҗғиҝ·пјҡйҖҖдј‘жңүжңӣ
-
#иҗЁе°”з“ҰеӨҡ#зү№жң—жҷ®дёҚдјҡиў«ж„ҹжҹ“пјҹзү№жң—жҷ®ж—©е·ІжіЁе°„дәҶз–«иӢ—пјҢзҫҺеӣҪйҳҙи°Ӣи—ҸдёҚдҪҸдәҶпјҒ
-
еӨ§йӨҗ|дёӯеӣҪз…Өзҹҝж–Үе·Ҙеӣўиө°иҝӣйӣ„е®ү дёәж–°еҢәе»әи®ҫиҖ…们еҘүдёҠж–ҮеҢ–еӨ§йӨҗ
-
жң¬жңә|жңүеўҷе°ұиғҪзңӢз”өеҪұ з”Ёе®ғеңЁе®¶жү“еҸ‘ж— иҒҠж—¶е…ү
-
иӮ–жҲҳ|еҸӨиЈ…жңҖеё…зҡ„з”·жҳҹпјҢжҲ‘иҜҙжҳҜдёӢйқўиҝҷеӣӣдҪҚдҪ 们еҗҢж„Ҹеҗ—пјҹ
-
[й’ҹдёҪзјҮ]й’ҹдёҪзјҮзңҹзҡ„еҝ«дә”еҚҒеІҒеҗ—пјҹзҙ§иә«иЈҷжҗӯзғӯиЈӨиә«жқҗдё°ж»ЎпјҢеҮҸиӮҘеүҚеҗҺеҲӨиӢҘдёӨдәә
-
жө·зӢ—|жІҷжј дёӯзҡ„зҢҺзү©еҢ®д№Ҹж—¶пјҢеҫҳеҫҠеңЁйӘ·й«…жө·еІёзҡ„жІҷжј зӢ®пјҢйқ еҗғжө·зӢ—з»ҙжҢҒз”ҹи®Ў
-
йІёеӘ’дҪ“|K12ж•ҷиӮІе“ҒзүҢвҖңе°‘е№ҙеҫ—еҲ°вҖқе®ҢжҲҗиҝ‘2дәҝе…ғBиҪ®иһҚиө„


















