ж•°еӯҰ|йҡҗи—ҸеңЁ ПҖ дёӯзҡ„зҫҺдёҪ( еӣӣ )
еңЁ 1962 е№ҙ 9 жңҲ 12 еҸ· пјҢ зәҰзҝ°иӮҜе°јиҝӘпјҲJohn F. KennedyпјүеҸ‘иЎЁдәҶдёҖзҜҮе…ідәҺеӨӘз©әи®ЎеҲ’зҡ„жј”и®І гҖӮ
вҖңдёәд»Җд№ҲйҖүжӢ©зҷ»жңҲдҪңдёәжҲ‘们зҡ„зӣ®ж ҮпјҹйӮЈд»–们д№ҹи®ёдјҡй—®дёәд»Җд№ҲжҲ‘们иҰҒзҷ»дёҠжңҖй«ҳзҡ„еұұеі°пјҹдёәд»Җд№Ҳ пјҢ иҰҒеңЁ35е№ҙеүҚ пјҢ йЈһи¶ҠеӨ§иҘҝжҙӢпјҹдёәд»Җд№Ҳиө–ж–ҜеӨ§еӯҰиҰҒдёҺеҫ·е…ӢиҗЁж–ҜеӨ§еӯҰз«һиөӣпјҹжҲ‘们еҶіе®ҡзҷ»жңҲ гҖӮ жҲ‘们еҶіе®ҡзҷ»жңҲ гҖӮ жҲ‘们еҶіе®ҡеңЁиҝҷеҚҒе№ҙй—ҙзҷ»дёҠжңҲзҗғ并е®һзҺ°жӣҙеӨҡжўҰжғі пјҢ 并йқһе®ғ们иҪ»иҖҢжҳ“дёҫ пјҢ иҖҢжӯЈжҳҜеӣ дёәе®ғ们еӣ°йҡҫйҮҚйҮҚ гҖӮ еӣ дёәиҝҷдёӘзӣ®ж Үе°ҶдҝғиҝӣжҲ‘们е®һзҺ°жңҖдҪізҡ„з»„з»Ү并жөӢиҜ•жҲ‘们顶尖зҡ„жҠҖжңҜе’ҢеҠӣйҮҸ пјҢ еӣ дёәиҝҷдёӘжҢ‘жҲҳжҲ‘们д№җдәҺжҺҘеҸ— пјҢ еӣ дёәиҝҷдёӘжҢ‘жҲҳжҲ‘们дёҚж„ҝжҺЁиҝҹ пјҢ еӣ дёәиҝҷдёӘжҢ‘жҲҳжҲ‘们еҝ—еңЁеҝ…еҫ— пјҢ е…¶д»–зҡ„жҢ‘жҲҳд№ҹжҳҜеҰӮжӯӨ гҖӮ вҖқ
еӣһжәҜиҝҮеҺ» пјҢ
жҺўз©¶
жқҘиҮӘеҸӨеёҢи…Ҡзҡ„йҳҝеҹәзұіеҫ·дҫҝжҳҜжңҖж—©и®Ўз®—еңҶе‘ЁзҺҮзҡ„жҷәиҖ…д№ӢдёҖ гҖӮ еҪ“ж—¶д»–еҸҜиғҪжҳҜи®ҫи®ЎеҲ¶йҖ иҪҰиҪ®зҡ„иҝҮзЁӢдёӯжҺҘи§ҰеҲ°иҝҷдёӘзҘһз§ҳзҡ„еёёж•° гҖӮ дҪҶжҳҜ他究з«ҹжҳҜжҖҺд№Ҳдј°и®ЎеҮә 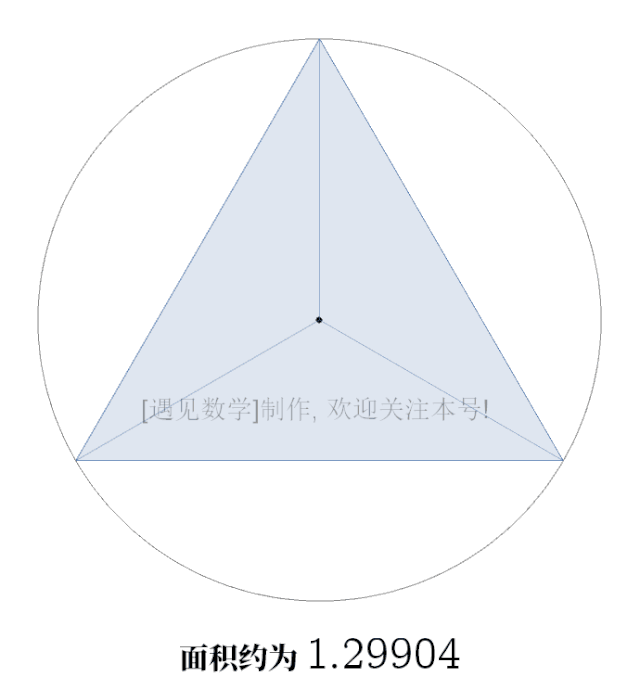
жң¬ж–ҮеӣҫзүҮ
д»–жүҖйҮҮз”Ёиҝҷз§ҚйҖҡиҝҮжӯЈеӨҡиҫ№еҪўзҡ„еҮ дҪ•з®—жі•жҳҜжңүз”Ёзҡ„ пјҢ еӣ дёәеҪ“ж—¶дәә们еҫҲйҡҫзІҫзЎ®ең°жөӢйҮҸжӣІйқў гҖӮ йҰ–е…Ҳ пјҢ д»–еҒҡдәҶе·ІзҹҘе‘Ёй•ҝзҡ„жӯЈж–№еҪўзҡ„еӨ–жҺҘеңҶ пјҢ 然еҗҺеңЁиҝҷдёӘеӨ–жҺҘеңҶзҡ„еӨ–йқўз”»з¬¬дәҢдёӘжӯЈж–№еҪў пјҢ ж»Ўи¶іеӨ–жҺҘеңҶжҳҜ第дәҢдёӘжӯЈж–№еҪўзҡ„еҶ…еҲҮеңҶ并жұӮеҮәиҜҘжӯЈж–№еҪўзҡ„е‘Ёй•ҝ гҖӮ иҝҷж ·д»–е°ұеҫ—еҲ°дәҶеңҶзҡ„е‘Ёй•ҝеә”иҜҘжҳҜд»ӢдәҺдёӨдёӘжӯЈж–№еҪўзҡ„е‘Ёй•ҝд№Ӣй—ҙ гҖӮ 然иҖҢеҲ©з”Ёиҝҷз§Қж–№жі•и®Ўз®—еҮәжқҘзҡ„дёӨдёӘжӯЈж–№еҪўзҡ„е‘Ёй•ҝе·®еҖјжҜ”иҫғеӨ§ гҖӮ еӣ жӯӨд»–еҸҲжҠҠжӯЈж–№еҪўжҚўжҲҗдә”иҫ№еҪўжқҘйҮҚж–°и®Ўз®—еңҶе‘Ёзҡ„дёҠдёӢз•Ң пјҢ д»–еҫ—еҲ°дәҶдёҖдёӘиҫғе°Ҹзҡ„еңҶе‘Ёзҡ„з•Ңйҷҗ гҖӮ д№ӢеҗҺ пјҢ д»–дёҚж–ӯең°еўһеҠ еңҶеҶ…еҲҮе’ҢеӨ–жҺҘеӨҡиҫ№еҪўзҡ„иҫ№ж•° гҖӮ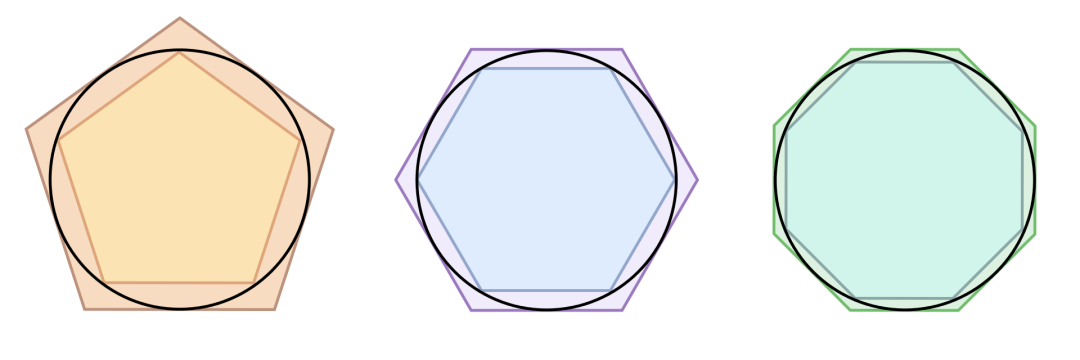
жң¬ж–ҮеӣҫзүҮ
йҳҝеҹәзұіеҫ·дҪҝз”Ёз©·з«ӯжі•йҖҡиҝҮи®Ўз®—еӨ–жҺҘеӨҡиҫ№еҪўе’ҢеҶ…жҺҘеӨҡиҫ№еҪўзҡ„е‘Ёй•ҝжқҘдј°и®Ў
жҺЁиҚҗйҳ…иҜ»
- иҝҳзҸ ж јж ј |еҘ№жҳҜгҖҠиҝҳзҸ гҖӢдёӯзҡ„иҖҒдҪӣзҲ·пјҢе’ҢдёҲеӨ«з»“е©ҡ20еӨҡе№ҙд»ҚжҒ©зҲұеҰӮеҲқпјҢи®©дәәзҫЎж…•
- жҳҺжҳҹе©ҡ姻|зӣҳзӮ№еЁұд№җеңҲдёӯзҡ„е№ІдәІпјҢеҲҳеҫ·еҚҺз»ҷж”ҜжҢҒпјҢе‘Ёжҳҹй©°з»ҷеҗҚж°”пјҢиҖҢд»–д»ӨдәәдҪңе‘•пјҒ
- ж”ҫйЈһиҮӘжҲ‘|гҖҠд№җйҳҹзҡ„еӨҸеӨ©гҖӢе®Ңж»ЎиҗҪ幕пјҢиҝҷдёӘиөӣжһңи·ҹдҪ еҝғзӣ®дёӯзҡ„HOT5е·®еҲ«еӨ§еҗ—пјҹ
- е’ҢеҢҲеҘҙ|вҖңдҪҶдҪҝйҫҷеҹҺйЈһе°ҶеңЁвҖқдёӯзҡ„вҖңйҫҷеҹҺйЈһе°ҶвҖқпјҢеҲ°еә•жҢҮзҡ„и°Ғзӯ”жқҺе№ҝжҳҜй”ҷзҡ„
- з»јиүә|гҖҠжј”е‘ҳиҜ·е°ұдҪҚгҖӢдёӯзҡ„е•ҶдёҡејҸеҗ№жҚ§пјҢдёҖзңӢе°ұзҹҘйҒ“йғҪжҳҜиҖҒжҚ§е“ҸдәҶ
- ж·ұжө·еҠЁзү©|зғӯеёҰйӣЁжһ—дёӯзҡ„йёҹзұ»е’Ңж·ұжө·дёӯзҡ„и •иҷ«пјҢжҲ‘们иҜҘдҝқжҠӨе“ӘдёӘпјҹ
- еә§жӨ…|иө°иҝӣеҗҙиҺ«ж„ҒзҺ°е®һдёӯзҡ„家пјҢйӨҗеҺ…жҳҜиҰҒеҪ“дјҡи®®е®Өз”ЁпјҹдёӨжҺ’еә§жӨ…иғҪеқҗеҮ еҚҒдәә
- и®әж–Ү|2020еҚҺж•°д№Ӣжҳҹйқ’е°‘е№ҙж•°еӯҰеӨ§дјҡе®ҢзҫҺ收е®ҳ ж ёжЎғзј–зЁӢеӯҰе‘ҳж–©иҺ·е…ЁеӣҪеүҚдёү
- иӢұиҜӯ|жө·еә•е°ҸзәөйҳҹеӯҰиӢұиҜӯжҗәжүӢиұҢиұҶжҖқз»ҙ дёәз”ЁжҲ·жҸҗдҫӣиӢұиҜӯж•°еӯҰеҸҢ科еҗҜи’ҷ
- йғҪеҸҜд»Ҙ|жңүзҪ‘еҸӢжҸҗй—®вҖңзӣёдәІиҠӮзӣ®дёӯзҡ„еҘіеҳүе®ҫпјҢйғҪжҳҜд»Һе“ӘйҮҢиҜ·жқҘзҡ„пјҹвҖқзңҹзӣёеҺҹжқҘжҳҜиҝҷж ·зҡ„
















