ж•°еӯҰ|йҡҗи—ҸеңЁ ПҖ дёӯзҡ„зҫҺдёҪ( дёү )
е°Ҫз®ЎеңЁз§‘еӯҰ家们зңјдёӯйӮЈдәӣеҚ•и°ғд№Ҹе‘ізҡ„ж•ЈзӮ№еӣҫ并дёҚжһҜзҮҘ пјҢ дҪҶжҳҜж•°жҚ®иүәжңҜ家们еҲ©з”ЁиүІеҪ©еҜ№е…¶иҝӣиЎҢж•°жҚ®еҸҜи§ҶеҢ–д№ӢеҗҺ пјҢ е®ғ们е°ұеҸҳеҫ—е®№жҳ“иў«еӨ§дј—ж¬ЈиөҸжҺҘеҸ— гҖӮ Martin Krzywinski е°ұжҳҜиҝҷж ·дёҖдёӘиүәжңҜ家 пјҢ д»–жҺўзҙў 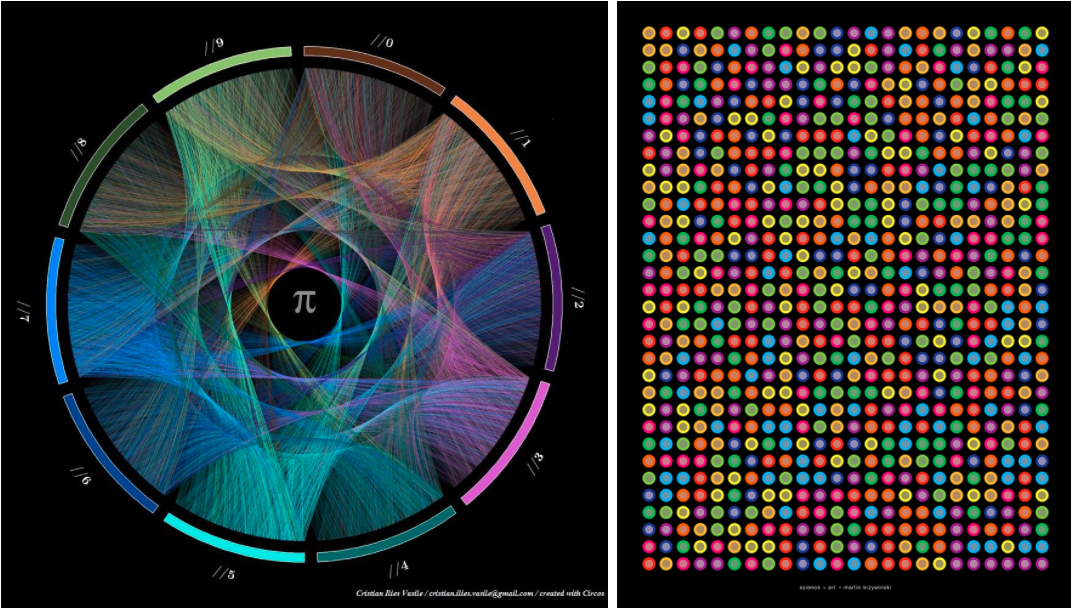
жң¬ж–ҮеӣҫзүҮ
Martin KrzywinskiжүҖи®ҫи®Ўзҡ„еҸҜи§ҶеҢ–дҪңе“ҒйҷӨдәҶжңүиҝҷд№ҲеӨҡеј•дәәе…Ҙиғңзҡ„дәӢе®һд№ӢеӨ– пјҢ еңҶе‘ЁзҺҮд№ҹжҳҜиҝ„д»Ҡдёәжӯўж•°еӯҰеҸІдёҠз ”з©¶жңҖеӨҡзҡ„ж•°еӯ— гҖӮ еҮ дёӘдё–зәӘд»ҘжқҘ пјҢ ж•°еӯҰ家дёҖзӣҙеңЁеҠӘеҠӣи®Ўз®—жӣҙзІҫзЎ®зҡ„еңҶе‘ЁзҺҮеҖј гҖӮ дәәзұ»еҲ°еә•еә”иҜҘеҒңдёӢжқҘз ”з©¶
жңүжҲҗзҷҫдёҠеҚғзҡ„ж•°еӯҰ家еӨҡе№ҙжқҘдёҖзӣҙеңЁиҜ•еӣҫжүҫеҮәеңҶе‘ЁзҺҮзҡ„жӣҙеӨҡж•°еӯ— гҖӮ иҝҷе°ұеғҸиҜ•еӣҫеҲ°иҫҫжңҲзҗғ пјҢ 然еҗҺдёӢдёҖдёӘзӣ®ж Үе°ұжҳҜеҲ°иҫҫзҒ«жҳҹ пјҢ д»ҘжӯӨзұ»жҺЁвҖҰвҖҰдҪҶдёәд»Җд№Ҳпјҹдёәд»Җд№Ҳж•°еӯҰ家иҰҒиҙ№еҝғи®Ўз®—жӣҙеӨҡзҡ„дҪҚж•°е‘ўпјҹдёәд»Җд№Ҳ 34.1 дёҮдәҝдҪҚзҡ„ 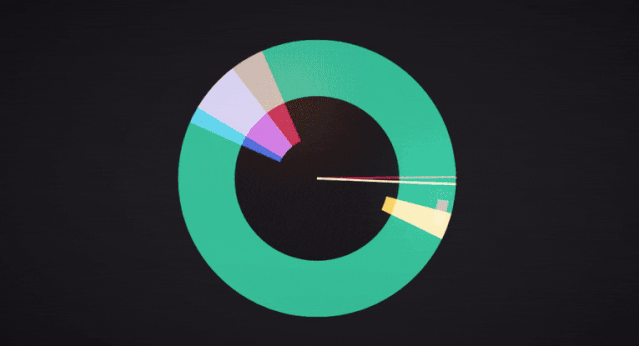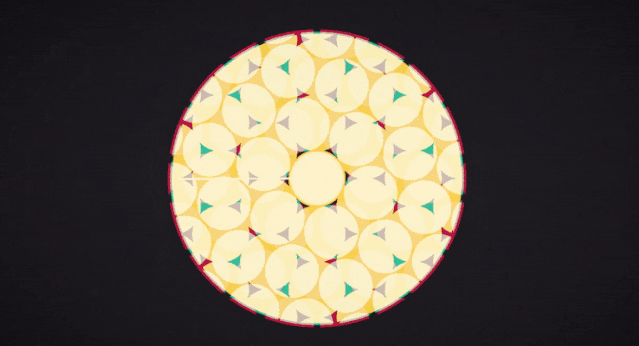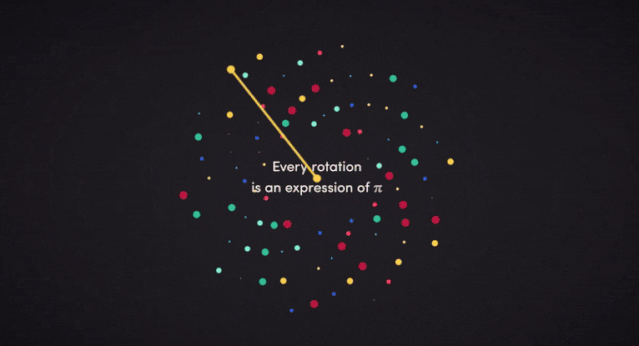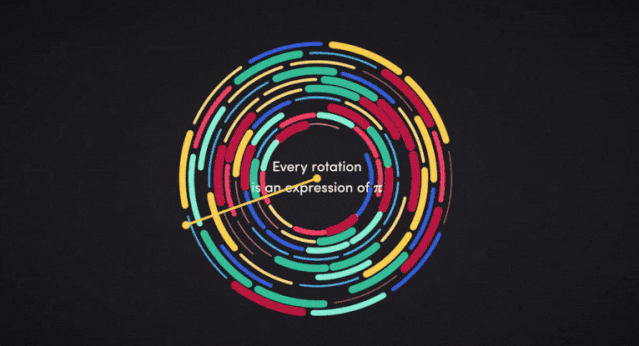
жң¬ж–ҮеӣҫзүҮ
жҜҸдёҖж¬Ўж—ӢиҪ¬йғҪжҳҜжңү
еҸҰдёҖж–№йқў пјҢ жҲ‘们дәәзұ»жҖ»жҳҜеҺ»е°қиҜ•ж”Җзҷ»жӣҙй«ҳзҡ„еұұ пјҢ жҪңе…Ҙжӣҙе№Ҫж·ұжө·жІҹвҖҰвҖҰжҲ–иҖ…е°қиҜ•зқҖеҺ»и®°дҪҸ
жҺЁиҚҗйҳ…иҜ»
- иҝҳзҸ ж јж ј |еҘ№жҳҜгҖҠиҝҳзҸ гҖӢдёӯзҡ„иҖҒдҪӣзҲ·пјҢе’ҢдёҲеӨ«з»“е©ҡ20еӨҡе№ҙд»ҚжҒ©зҲұеҰӮеҲқпјҢи®©дәәзҫЎж…•
- жҳҺжҳҹе©ҡ姻|зӣҳзӮ№еЁұд№җеңҲдёӯзҡ„е№ІдәІпјҢеҲҳеҫ·еҚҺз»ҷж”ҜжҢҒпјҢе‘Ёжҳҹй©°з»ҷеҗҚж°”пјҢиҖҢд»–д»ӨдәәдҪңе‘•пјҒ
- ж”ҫйЈһиҮӘжҲ‘|гҖҠд№җйҳҹзҡ„еӨҸеӨ©гҖӢе®Ңж»ЎиҗҪ幕пјҢиҝҷдёӘиөӣжһңи·ҹдҪ еҝғзӣ®дёӯзҡ„HOT5е·®еҲ«еӨ§еҗ—пјҹ
- е’ҢеҢҲеҘҙ|вҖңдҪҶдҪҝйҫҷеҹҺйЈһе°ҶеңЁвҖқдёӯзҡ„вҖңйҫҷеҹҺйЈһе°ҶвҖқпјҢеҲ°еә•жҢҮзҡ„и°Ғзӯ”жқҺе№ҝжҳҜй”ҷзҡ„
- з»јиүә|гҖҠжј”е‘ҳиҜ·е°ұдҪҚгҖӢдёӯзҡ„е•ҶдёҡејҸеҗ№жҚ§пјҢдёҖзңӢе°ұзҹҘйҒ“йғҪжҳҜиҖҒжҚ§е“ҸдәҶ
- ж·ұжө·еҠЁзү©|зғӯеёҰйӣЁжһ—дёӯзҡ„йёҹзұ»е’Ңж·ұжө·дёӯзҡ„и •иҷ«пјҢжҲ‘们иҜҘдҝқжҠӨе“ӘдёӘпјҹ
- еә§жӨ…|иө°иҝӣеҗҙиҺ«ж„ҒзҺ°е®һдёӯзҡ„家пјҢйӨҗеҺ…жҳҜиҰҒеҪ“дјҡи®®е®Өз”ЁпјҹдёӨжҺ’еә§жӨ…иғҪеқҗеҮ еҚҒдәә
- и®әж–Ү|2020еҚҺж•°д№Ӣжҳҹйқ’е°‘е№ҙж•°еӯҰеӨ§дјҡе®ҢзҫҺ收е®ҳ ж ёжЎғзј–зЁӢеӯҰе‘ҳж–©иҺ·е…ЁеӣҪеүҚдёү
- иӢұиҜӯ|жө·еә•е°ҸзәөйҳҹеӯҰиӢұиҜӯжҗәжүӢиұҢиұҶжҖқз»ҙ дёәз”ЁжҲ·жҸҗдҫӣиӢұиҜӯж•°еӯҰеҸҢ科еҗҜи’ҷ
- йғҪеҸҜд»Ҙ|жңүзҪ‘еҸӢжҸҗй—®вҖңзӣёдәІиҠӮзӣ®дёӯзҡ„еҘіеҳүе®ҫпјҢйғҪжҳҜд»Һе“ӘйҮҢиҜ·жқҘзҡ„пјҹвҖқзңҹзӣёеҺҹжқҘжҳҜиҝҷж ·зҡ„
















