江苏龙网

  1. 首页 > 生活 > >

「高考」怎么办？从必考热点开始吴国平：2020年高考就剩下三个月左右

江苏龙网_原题是：吴国平：2020年高考就剩下三个月左右 ， 怎么办？从必考热点开始
「高考」怎么办？从必考热点开始吴国平：2020年高考就剩下三个月左右
文章图片

再过三个月左右 ， 2020年高考就来临 ， 剩下的这些时间对于每一位考生来说 ， 显得异常珍贵 。 因此 ， 如何用好每分每秒 ， 提高复习效率 ， 更应是考生关注的事情 。 像高考数学的复习 ， 重难点和热点非常多 ， 但我们就必须抓住一些必考点 ， 如立体几何相关的知识点和题型 。
我们对全国各省市高考数学当中与立体几何有关题型进行分析 ， 特别是对考查内容、考查方式、考查重点进行了整体评析 ， 对立体几何的知识定理、技能要求、解题方法、数学思想及能力要求进行了分析 ， 总结立体几何在高考中的题型分布、分值比例等 ， 这些都能帮助大家提高数学成绩 。
立体几何相关的试题注重知识与能力融合的命题思路 ， 在试题命制方面体现三个突出 ， 即突出对立体几何主要基础知识、基本技能和基本思想方法的考查；突出对通性、通法的考查；突出对空间想象能力、推理论证能力 ， 以及化归和转化能力的考查 。
其实不管是哪种数学知识 ， 考生都要学会挖掘知识间的内在联系 ， 不断创新 ， 抓住要点 ， 就可以提高复习效率 。
「高考」怎么办？从必考热点开始吴国平：2020年高考就剩下三个月左右
文章图片

立体几何有关的高考数学试题分析 ， 讲解1：
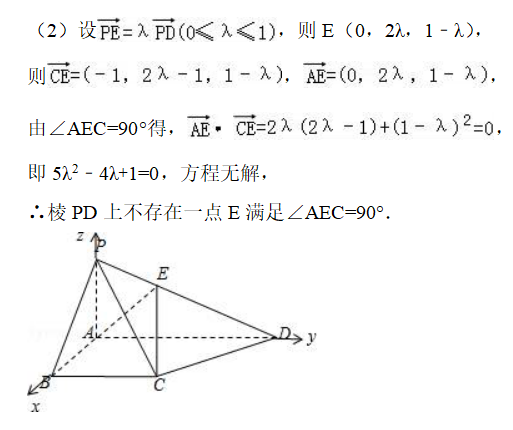
如图 ， 在四棱锥P﹣ABCD中 ， 底面ABCD为直角梯形 ， ∠ABC=∠BAD=90° ， 且PA=AB=BC=AD/2=1 ， PA⊥平面ABCD．
（1）求PB与平面PCD所成角的正弦值；
（2）棱PD上是否存在一点E满足∠AEC=90°？
「高考」怎么办？从必考热点开始吴国平：2020年高考就剩下三个月左右
文章图片

「高考」怎么办？从必考热点开始吴国平：2020年高考就剩下三个月左右
文章图片

考点分析：
直线与平面所成的角；直线与平面垂直的判定．
题干分析：
（1）以A为坐标原点建立空间直角坐标系 ， 求出和平面PCD的法向量 ， 则即为所求；
（2）假设存在E符合条件 ， 列出方程 ， 判定方程在[0 ， 1]上是否有解即可得出结论．
「高考」怎么办？从必考热点开始吴国平：2020年高考就剩下三个月左右
文章图片

立体几何有关的高考数学试题分析 ， 讲解2：
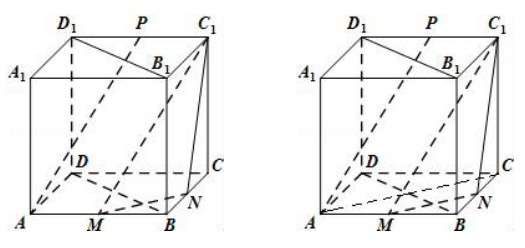
如图 ， 在正方体ABCD﹣A1B1C1D1中 ， M ， N ， P分别为棱AB ， BC ， C1D1的中点．
求证：（1）AP∥平面C1MN；
（2）平面B1BDD1⊥平面C1MN．
「高考」怎么办？从必考热点开始吴国平：2020年高考就剩下三个月左右
文章图片

证明：（1）在正方体ABCD﹣A1B1C1D1中 ，
∵M ， N ， P分别为棱AB ， BC ， C1D1的中点 ，
∴AM=PC1 ，
又AM∥CD ， PC1∥CD ， 故AM∥PC1 ，
∴四边形AMC1P为平行四边形 ，
∴AP∥C1M ，
又AP?平面C1MN ， C1M?平面C1MN ，
∴AP∥平面C1MN．
（2）连结AC ， 在正方形ABCD中 ， AC⊥BD ，
又M、N分别为棱AB、BC的中点 ，
∴MN∥AC ，
∴MN⊥BD ，
在正方体ABCD﹣A1B1C1D1中 ， DD1⊥平面ABCD ，
又MN?平面ABCD ，
∴DD1⊥MN ，
而DD1∩DB=D ， DD1、DB?平面BDD1B1 ，
∴MN⊥平面BDD1B1 ，
又MN?平面C1MN ，
∴平面B1BDD1⊥平面C1MN．


推荐阅读


上一篇：【医生】父母着急带娃去医院，医生检查后笑出声儿子出生“没睁过眼”

下一篇：怎样评价QQ兴趣部落