一文讲透微积分的本质( 三 ) _微积分

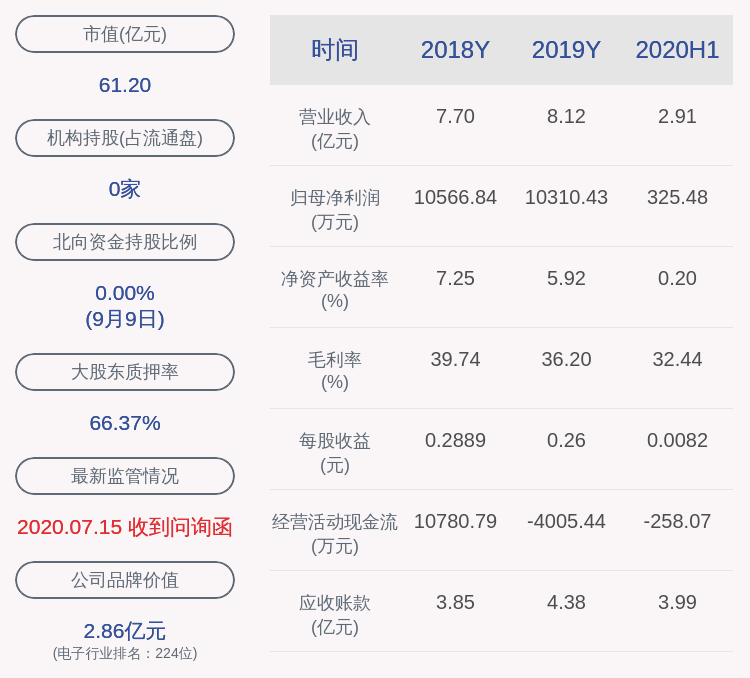
另一方面，使用积分公式可得
这与梯形面积公式计算出来的结果完全相等。
下面，我们来看抛物线的例子。
图 103 是抛物线部分图像。计算从x =1 到x = 2 的面积。这次的图无法再使用“梯形面积公式”，所以只能使用积分。

文章插图
套用积分公式得出
看，一瞬间就可以得出答案。没有积分似乎很难计算出来。不得不说，积分真是太厉害了。
顺便说一下，前文说到圆的面积、球的表面积时出现了公式

文章插图
这里只是把x换成了r，是幂函数的积分公式的特殊情况（分别为β =1、β = 2）。
03
近似和忽略
微积分的本质在于近似与忽略。近似指的是忽略一些东西，只给出大概的答案。
即使是复杂的形状，也可以将其视为简单长方形的组合（积分），函数在局部可以视为切线或者抛物线（微分），这个思考角度才是微积分的要领。
重要的是不要在意细节。不在意细小的部分，“用直线段近似函数图像”就可以搞清楚容积最大的冰激凌蛋卷筒是什么形状，也可以“把曲线看作折线的组合”来计算悬链线的长度。虽然整体计算很难，但分成较小的部分就会变成简单的累加。这就是微积分厉害之处。
实际上，这种思想并不仅限于微积分，可以说整个数学都是这样的。微积分则是了解该方法有效性的最好素材。
实际上，我们居住的现实世界中，近似可以说是无处不在。比如，不存在无限小的东西（无法比基本粒子更小），宇宙也并非无限广阔。
但是，在实际的微积分中，要考虑无限小的量，或者无限大的空间，这是近似。忽略基本粒子的大小，搁置宇宙的边界限制，这种想法或许与事实相悖，但是这种方法给我们带来的恩惠却不可估量。
微分积分的内容是从细致分割图形开始讲起的，之后又讲到自然常数e，最后又到悬链线的长度。读到这里，大家是不是已经自然而然地认可“近似和忽略”的思考方法呢？如果是的话，那么这就是很大的进步了。

文章插图
《简单微积分：学校未教过的超简易》
作者：[日]神永正博
译者：李慧慧
仅用“阅读”就能理解微积分原理，无须背诵公式、烦琐计算，传授日本微积分入门的“巧妙思路” 。
书为微积分入门科普读物，书中以微积分的“思考方法”为核心，以生活例子通俗讲解了微积分的基本原理、公式推导以及实际应用意义，解答了微积分初学者遭遇的常见困惑。

文章插图
《微积分的历程：从牛顿到勒贝格》
作者：邓纳姆
译者：李伯民汪军张怀勇
本书荣获“第七届文津图书奖推荐书目” 。
这不是一本数学家的传记，而是一座展示微积分宏伟画卷的陈列室。书中的每一个结果，从牛顿的正弦函数的推导，到伽玛函数的表示，再到贝尔的分类定理，无一不处于各个时代的研究前沿，至今还闪烁着耀眼夺目的光芒。

文章插图
《普林斯顿微积分读本（修订版）》
《普林斯顿数学分析读本》
《普林斯顿概率论读本》
作者：[美] 史蒂文·J. 米勒、拉菲·格林贝格、史蒂文·J. 米勒
译者：李馨
风靡美国普林斯顿大学的数学课程读本，教你怎样在数学考试中获得高分，用大量例子和代码全面探讨数学问题提供课程视频和讲义。被誉为“普林斯顿读本”三剑客。