жўҜеәҰзӣҙж–№еӣҫ(HOG)з”ЁдәҺеӣҫеғҸеӨҡеҲҶзұ»е’ҢеӣҫеғҸжҺЁиҚҗ( дәҢ )
зҺ°еңЁи®©жҲ‘们иҖғиҷ‘дёӢйқўзҡ„еӣҫеғҸ пјҢ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
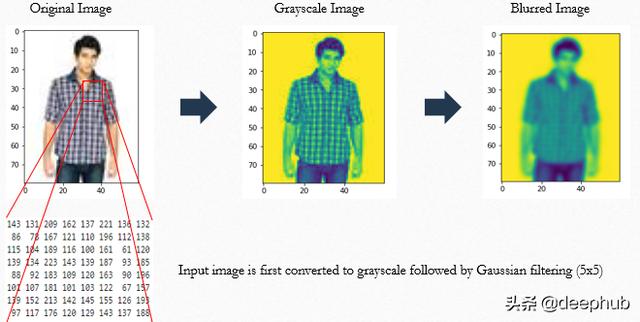
и®©жҲ‘们еҒҮи®ҫзәўиүІзҡ„ж–№жЎҶз”Ё8x8зҹ©йҳөиЎЁзӨә пјҢ жҜҸдёӘеҚ•е…ғж јдёӯйғҪжңүж•°еӯ— гҖӮ еңЁиҝӣиЎҢеӣҫеғҸзү№еҫҒе·ҘзЁӢд№ӢеүҚ пјҢ е»әи®®еҒҡд»ҘдёӢеҮ 件дәӢ:
1. Resize:е°ҶжүҖжңүеӣҫеғҸи°ғж•ҙдёәз»ҹдёҖеҪўзҠ¶ пјҢ д»ҘйҒҝе…Қд»»дҪ•дёҺи®Ўз®—зӣёе…ізҡ„йҡҗжӮЈ гҖӮ еңЁжң¬дҫӢдёӯ пјҢ жүҖжңүеӣҫеғҸзҡ„еҪўзҠ¶з»ҹдёҖ(60x80) гҖӮ еҰӮжһңжӮЁжғіжү§иЎҢи°ғж•ҙеӨ§е°Ҹж“ҚдҪң пјҢ иҜ·еҸӮйҳ…д»ҘдёӢеҶ…е®№:
def resize_image(img,ids):return cv.resize(img, (60, 80),interpolation =cv.INTER_LINEAR)all_images_resized = [[resize_image(x,y),y] for x,y in all_images]len(all_images_resized)1. Normalize :д»ҘйҒҝе…Қдә®еәҰгҖҒеҜ№жҜ”еәҰжҲ–е…¶д»–з…§жҳҺж•ҲжһңйҖ жҲҗзҡ„еҪұе“Қ гҖӮ
1. FilteringпјҡиҖғиҷ‘еҮ дёӘзӣёйӮ»еғҸзҙ пјҢ иҖҢдёҚжҳҜеҚ•дёҖеғҸзҙ еҖјдҪңдёәеғҸзҙ зҡ„зңҹе®һеҖј гҖӮ й«ҳж–Ҝж»ӨжіўеҜ№дёӯеҝғеғҸзҙ жқғйҮҚжңҖеӨ§ пјҢ еҜ№зӣёйӮ»еғҸзҙ жқғйҮҚжҢүwгҖҒrгҖҒtйҖ’еҮҸ пјҢ еҚіж №жҚ®зӘ—еҸЈеӨ§е°ҸзЎ®е®ҡдёҺдёӯеҝғеғҸзҙ зҡ„и·қзҰ» гҖӮ
гҖҗжўҜеәҰзӣҙж–№еӣҫ(HOG)з”ЁдәҺеӣҫеғҸеӨҡеҲҶзұ»е’ҢеӣҫеғҸжҺЁиҚҗгҖ‘жңҖеҗҺеҜ№ж»ӨжіўеҗҺзҡ„еӣҫеғҸиҝӣиЎҢеҰӮдёӢи®Ўз®—:
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
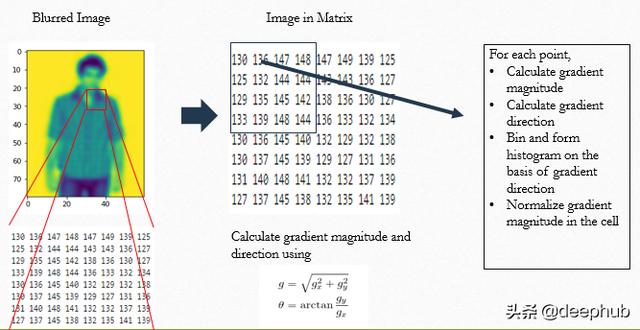
е°Ҷж•ҙдёӘеӣҫеғҸеҲҶжҲҗиӢҘе№Іеқ—(b) гҖӮ дёҖдёӘе…ёеһӢзҡ„еқ—жҳҜдёҠйқўжҸҗеҲ°зҡ„зәўжЎҶ гҖӮ жӯӨеӨ– пјҢ е…¶д»–еқ—еҸҜд»ҘзңӢдҪңжҳҜй»‘зӣ’дёӯжҸҗеҲ°зҡ„еҚ•е…ғж ј(c)зҡ„йӣҶеҗҲ гҖӮ дёҠеӣҫдёӯ пјҢ bзҡ„е°әеҜёжҳҜ8x8, cзҡ„е°әеҜёжҳҜ4x4
жҺҘдёӢжқҘ пјҢ еҜ№дәҺжҜҸдёӘеҚ•е…ғж ј пјҢ и®Ўз®—еҚ•е…ғж јдёӯжҜҸдёӘзӮ№зҡ„жўҜеәҰеӨ§е°Ҹе’Ңж–№еҗ‘(дёәдәҶз®ҖеҚ•иө·и§Ғ пјҢ жўҜеәҰеӨ§е°ҸеҸҜд»Ҙз®ҖеҚ•ең°еҒҮи®ҫдёәSobelеҜјж•°жҲ–д»»ж„ҸдёӨдёӘиҝһз»ӯзҡ„xе’ҢyеғҸзҙ еҖјд№Ӣй—ҙзҡ„е·®) гҖӮ 然еҗҺеҪўжҲҗеӨ§е°Ҹдёәnзҡ„зӣҙж–№еӣҫ пјҢ е°ҶжўҜеәҰйҮҸзә§еҖјд»Һw.r.tжўҜеәҰж–№еҗ‘иҝӣиЎҢеӨ„зҗҶ гҖӮ жңҖеҗҺж №жҚ®и§„еҲҷеҜ№зӣҙж–№еӣҫиҝӣиЎҢеҪ’дёҖеҢ– пјҢ еҪўжҲҗдёҖдёӘnз»ҙеҗ‘йҮҸ гҖӮ
еҜ№дәҺдёҖдёӘеҚ•е…ғж ј пјҢ жҲ‘们еҫ—еҲ°дёҖдёӘnз»ҙеҗ‘йҮҸ гҖӮ жҺҘдёӢжқҘзҡ„ж“ҚдҪңжҳҜйҖҡиҝҮеҗ‘еҸіз§»еҠЁ50%йҮҚеҸ зҡ„еӣҫеғҸеқ—е’Ңеҗ‘дёӢ移50%йҮҚеҸ зҡ„еӣҫеғҸеқ—жқҘиҰҶзӣ–ж•ҙдёӘеӣҫеғҸ гҖӮ
жңҖеҗҺ пјҢ е°ҶжүҖжңүиҝҷдәӣзӣҙж–№еӣҫдёІиҒ”иө·жқҘ пјҢ еҪўжҲҗдёҖдёӘдёҖз»ҙеҗ‘йҮҸ пјҢ з§°дёәHOGзү№еҫҒжҸҸиҝ°з¬Ұ гҖӮ
HOGеҸҜд»ҘйҖҡиҝҮдёӢйқўзҡ„д»Јз Ғж®өиҝӣиЎҢе®һзҺ° гҖӮ
##HOG Descriptor#Returns a 1D vector for an imageppcr = 8ppcc = 8hog_images = []hog_features = []for image in tqdm(train_images): blur = cv.GaussianBlur(image,(5,5),0) #Gaussian Filtering fd,hog_image = hog(blur, orientations=8, pixels_per_cell=(ppcr,ppcc),cells_per_block=(2,2),block_norm= вҖҳL2вҖҷ,visualize=True) hog_images.append(hog_image) hog_features.append(fd)hog_features = np.array(hog_features)hog_features.shapeеҸӮж•°
еҜ№иҝҷдёӘй—®йўҳпјҡ-еқ—еӨ§е°Ҹдёә16x16
-еҚ•е…ғж јеӨ§е°Ҹдёә8x8
иҝҷдҪҝеҫ—pixelpercell = (8x8)并且cellsperblock = (2x2)
-orientations(=8)жҳҜжҜҸдёӘеҚ•е…ғж јзҡ„зӣҙж–№еӣҫе®№еҷЁзҡ„ж•°йҮҸ гҖӮ еңЁиҝҷ8дёӘе®№еҷЁдёӯе°Ҷж”ҫзҪ®16дёӘжўҜеәҰеҖј пјҢ 并е°Ҷе®ғ们添еҠ еҲ°жҜҸдёӘе®№еҷЁдёӯд»ҘиЎЁзӨәиҜҘж–№еҗ‘е®№еҷЁзҡ„жўҜеәҰеӨ§е°Ҹ гҖӮ еҪ“дёӨдёӘиҝһз»ӯз®ұеӯҗд№Ӣй—ҙзҡ„жўҜеәҰеҲҶй…ҚеҸ‘з”ҹеҶІзӘҒж—¶ пјҢ йҖҡеёёйҖҡиҝҮжўҜеәҰжҸ’еҖјжқҘеҜ№жўҜеәҰеҖјиҝӣиЎҢжҠ•зҘЁ гҖӮ
-block_norm ="L1" гҖӮ е…¶д»–еҸӮж•°жңүL1еҪ’дёҖеҢ–жҲ–L2-Hys(Hysteresis) гҖӮ L2-HysеңЁжҹҗдәӣжғ…еҶөдёӢеҸҜд»ҘеҮҸе°‘еҷӘйҹі гҖӮ е®ғдҪҝз”Ёl2 -иҢғж•°жқҘе®ҢжҲҗ пјҢ 然еҗҺе°ҶжңҖеӨ§еҖјйҷҗеҲ¶дёә0.2 пјҢ 并дҪҝз”Ёl2 -иҢғж•°жқҘйҮҚж–°еҪ’дёҖеҢ– гҖӮ
#normalization by 'L2-Hys'out = block / np.sqrt(np.sum(block ** 2) + eps ** 2)out = np.minimum(out, 0.2)out = out / np.sqrt(np.sum(out ** 2) + eps ** 2)еҪ“е®һйҷ…еӣҫеғҸеҪўзҠ¶дёә60x80 пјҢ еқ—еӨ§е°Ҹдёә16x16ж—¶ пјҢ жҖ»е…ұе°ҶеҲӣе»ә6x9 = 54дёӘеқ—(иҖғиҷ‘еҲ°x,yдёӯд»»ж„ҸдёҖжӯҘ50%зҡ„йҮҚеҸ ) пјҢ иҖҢеңЁжҜҸдёӘеқ—дёӯжҲ‘们е°Ҷжңү4дёӘеҚ•е…ғж ј пјҢ жҜҸдёӘеҚ•е…ғж јжңү8дёӘзӣҙж–№еӣҫ гҖӮ еӣ жӯӨ пјҢ зү№еҫҒеҗ‘йҮҸзҡ„й•ҝеәҰдёә54x4x8 = 1728












![[з»ҝиұҶ]з”·дәәжғіиҰҒй•ҝеҜҝпјҢ5件вҖңиҖ—йҳівҖқзҡ„дәӢиҰҒвҖңиҲҚејғвҖқпјҢдёҖдәӣдәәиЎЁзӨәеҫҲйҡҫеҒҡеҲ°](http://img88.010lm.com/img.php?https://image.uc.cn/s/wemedia/s/2020/26fa2bbcc60faf5ef39679c3f1999fd3.jpg)




