江苏龙网

  1. 首页 > 人文 > >

数据不平衡问题( 二 )


数据不平衡问题文章插图
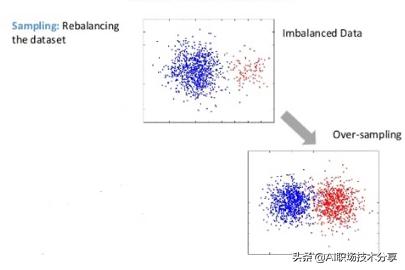
过采样 – 随机复制
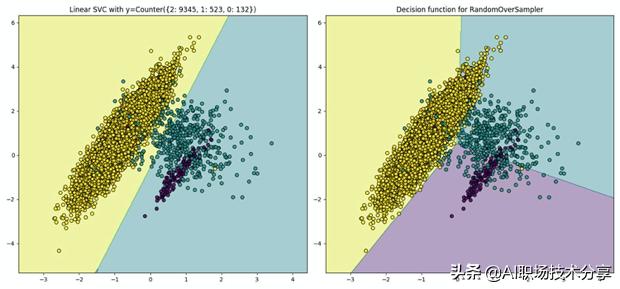
?随机复制即对少量样本进行复制后达到样本均衡的效果以提升模型效果 。 如下图所示 ， 在进行复制前 ， Linear SVC只找到一个超平面——即认为样本集中仅两类样本 。 随机复制后 ，Linear SVC找到了另外两 个超平面 。
数据不平衡问题文章插图
过采样 – 样本构建
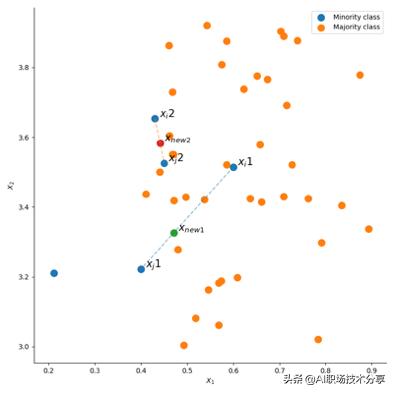
?在随机过采样的基础上 ， 通过样本构造一方面降低了直接复制样本带来的过拟合风险 ， 另一方面 实现了样本均衡 。 比较典型的样本构造方法有SMOTE(Synthetic minority over-sampling technique)及其衍生算法 。
?SMOTE算法通过从少量样本集合中筛选的样本x_i和x_j及对应的随机数0 < < 1 ， 通过两个样本间的关系来构建新的样本x_n=x_i+λ(x_j-x_i) 。
?由于SMOTE算法构建样本时 ， 是随机的进行样本点的组 合和参数设置 ， 因此会有以下2个问题:
?1)在进行少量样本构造时 ， 未考虑样本分布情况 ， 对于少量样本比较稀 疏的区域 ， 采用与少量样本比较密集的区域相同的概率进行构建 ， 会使构建 的样本可能更接近于边界;只是简单的在同类近邻之间插值 ， 并没有考虑少 数类样本周围多数类样本的分布情况 。
?2)当样本维度过高时 ， 样本在空间上的分布会稀疏 ， 由此可能使构建的 样本无法代表少量样本的特征 。
数据不平衡问题文章插图
?针对上述问题 ， 衍生出SMOTEBoost、Borderline-SMOTE、Kmeans-SMOTE等 。
a)SMOTEBoost把SMOTE算法和Boost算法结合 ， 在每一轮分类学习过程中增加对少数类的样本的权重 ， 使得基学习器 (base learner) 能够更好地关注到少数类样本 。
b)Borderline-SMOTE在构造样本时考虑少量样本周围的样本分布 ， 选择少量样本集合(DANGER集合)——其邻居节点 既有多量样本也有少量样本 ， 且多量样本数不大于少量样本的点来构造新样本 。
c) Kmeans-SMOTE包括聚类、过滤和过采样三步 。 利用Kmeans算法完成聚类后 ， 进行样本簇过滤 ， 在每个样本簇内利 用SMOTE算法构建新样本 。
数据不平衡问题文章插图
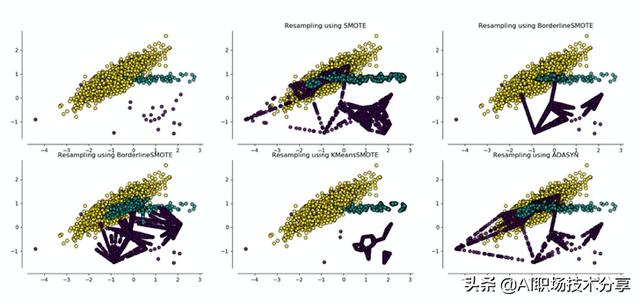
?通过比较不同算法得到的样本构造 ， 可得以下结论:
①利用样本构建的方法 ， 可以得到新的少量样本;
②利用不同算法构建的新样本在数量和分布上不同 ， 其中利用SMOTE算法构建的新样本 ， 由于没有考虑原始样本分布情况 ， 构建的新 样本会受到“噪声”点的影响 。 同样ASASYN算法只考虑了分布密度而未考虑样本分布 ， 构建的新样本也会受到“噪声”点的影响 。Borderline-SMOTE算法由于考虑了样本的分布 ， 构建的新样本能够比较好的避免“噪声”点的影响 。 Kmeans-SMOTE算法由于要去寻找簇 后再构建新样本 ， 可构建的新样本数量受限 。
?注:“噪声”点对应类别上属于少量样本 ， 但是分布上比较靠近边界或者与多量样本混为一起 。
样本均衡 – 模型算法
?上述的过采样和欠采样都是从样本的层面去克服样本的不平衡 ， 从算法层面来说 ， 克服样本不平 衡 。 在现实任务中常会遇到这样的情况:不同类型的错误所造成的后果不同 。
?例如:在医疗诊断中 ， 错误地把患者诊断为健康人与错误地把健康人诊断为患者 ， 看起来都是犯 了“一次错误” ， 但是后者的影响是增加了进一步检查的麻烦 ， 前者的后果却可能是丧失了拯救生命 的最佳时机;
【数据不平衡问题】?再如 ， 门禁系统错误地把可通行人员拦在门外 ， 将使得用户体验不佳 ， 但错误地把陌生人放进门 内 ， 则会造成严重的安全事故;


推荐阅读


上一篇：在 iPhone 12 Pro Max 上，玩天涯明月刀手游是怎样一种体验？

下一篇：如何优化 TensorFlow Lite 运行时内存？