ж·ұеәҰеҚ·з§Ҝ|ж·ұе…ҘеҚ·з§ҜзҘһз»ҸзҪ‘з»ңпјҡй«ҳзә§еҚ·з§ҜеұӮеҺҹзҗҶе’Ңи®Ўз®—зҡ„еҸҜи§ҶеҢ–( дәҢ )
е°ҶжүҖжңүж·»еҠ зҡ„еғҸзҙ з”Ё0д»Је…ҘеҗҺпјҢеҶҚеҜ№ж”ҫеӨ§еҗҺзҡ„feature mapиҝӣиЎҢжҷ®йҖҡеҚ·з§ҜгҖӮиҝҷе°ұжҳҜжҲ‘们еҰӮдҪ•еңЁеҜ№feature mapжү§иЎҢеҚ·з§Ҝж“ҚдҪңзҡ„еҗҢж—¶еўһеҠ е®ғзҡ„еӨ§е°ҸгҖӮ
ж–Үз« еӣҫзүҮ
дёҠйҮҮж ·
гҖҗ ж·ұеәҰеҚ·з§Ҝ|ж·ұе…ҘеҚ·з§ҜзҘһз»ҸзҪ‘з»ңпјҡй«ҳзә§еҚ·з§ҜеұӮеҺҹзҗҶе’Ңи®Ўз®—зҡ„еҸҜи§ҶеҢ–гҖ‘еҜ№дәҺдёҠйҮҮж ·еұӮпјҢжҲ‘们еңЁж·»еҠ еғҸзҙ зҡ„дҪҚзҪ®еӨҚеҲ¶еҺҹе§ӢеғҸзҙ еҖјгҖӮеӣ жӯӨжҜҸдёӘеғҸзҙ е°Ҷиў«еӨҚеҲ¶4ж¬ЎеҰӮжһңжҲ‘们еҒҡзҡ„жҳҜдёҖдёӘ2еҖҚжү©е……гҖӮд»ҺжҠҖжңҜдёҠи®ІпјҢеҰӮжһңжҲ‘们еҸӘиҖғиҷ‘дёҠйҮҮж ·еұӮпјҢеңЁеҜ№feature mapиҝӣиЎҢж”ҫеӨ§еҗҺе°ұдёҚеӯҳеңЁеҚ·з§ҜгҖӮдҪҶжҳҜжҲ‘们йҖҡеёёеңЁдёҠйҮҮж ·еұӮд№ӢеҗҺеҠ дёҠеҚ·з§ҜеұӮиҝҷж ·зҪ‘з»ңе°ұжңүдәҶдёҖдәӣеӯҰд№ иғҪеҠӣеӣ дёәдёҠйҮҮж ·еұӮжң¬иә«жІЎжңүд»»дҪ•еҸӮж•°гҖӮ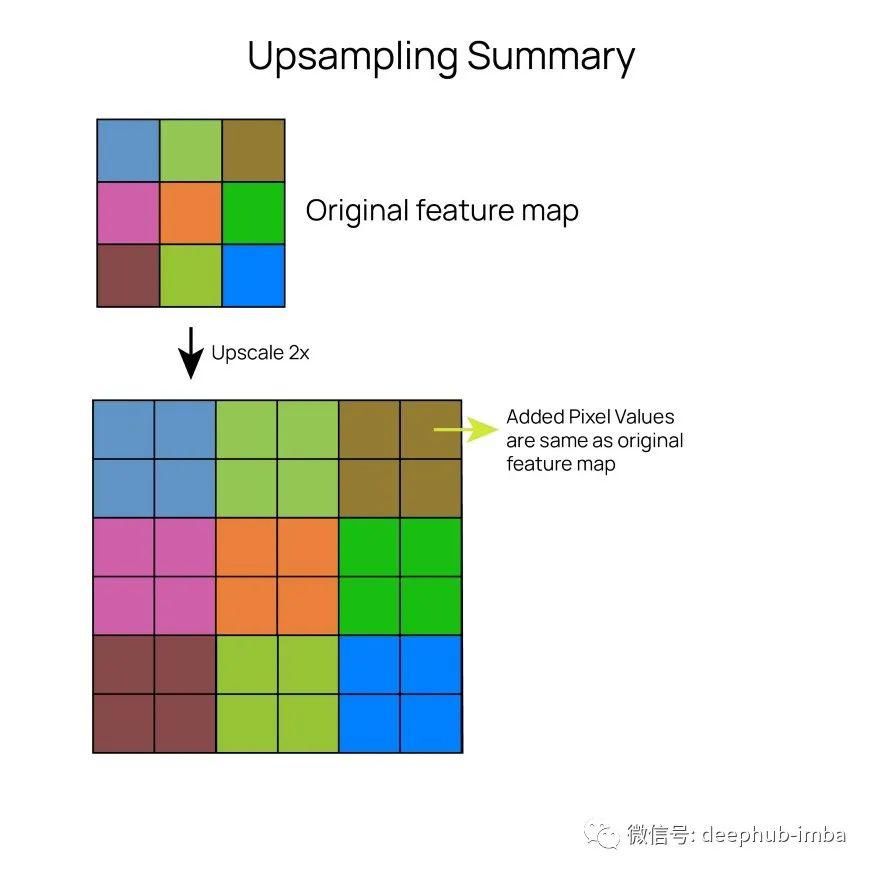
ж–Үз« еӣҫзүҮ
иҝҷдёӨеұӮеңЁзҪ‘з»ңзҘһз»ҸзҪ‘з»ңдёӯиў«е№ҝжіӣдҪҝз”ЁпјҢзҪ‘з»ңзҘһз»ҸзҪ‘з»ңиҜ•еӣҫиҫ“еҮәдёҺеҺҹе§Ӣиҫ“е…ҘзӣёеҗҢеӨ§е°Ҹзҡ„feature mapгҖӮдёҖиҲ¬жғ…еҶөдёӢпјҢдјҡжңүдёҖдәӣжҷ®йҖҡзҡ„еҚ·з§Ҝе’Ңжұ еҢ–еұӮпјҢиҝҷдјҡеҮҸе°Ҹfeature mapзҡ„еӨ§е°ҸгҖӮеңЁиҝҷд№ӢеҗҺпјҢжҲ‘们е°Ҷеј•е…ҘеҸҚеҚ·з§ҜеұӮпјҢе°ҶеӨ§е°ҸеўһеҠ еӣһеҺҹжқҘзҡ„еӨ§е°ҸгҖӮиҜӯд№үеҲҶеүІCNNsгҖҒU-NetгҖҒGANsзӯүдҪҝз”ЁеҸҚеҚ·з§ҜеұӮгҖӮ
з©әжҙһеҚ·з§ҜDilated (Atrous) Convolution
еңЁз ”究з•ҢдёӯпјҢз©әжҙһеҚ·з§Ҝд№ҹиў«з§°дёәдјёзј©еҚ·з§ҜгҖӮеңЁз©әжҙһеҚ·з§ҜдёӯпјҢжҲ‘们жң¬иҙЁдёҠиҜ•еӣҫеўһеҠ жҜҸдёӘж ёзҡ„йқўз§ҜпјҢеҗҢж—¶дҝқжҢҒжҜҸдёӘж ёзҡ„е…ғзҙ ж•°йҮҸе®Ңе…ЁзӣёеҗҢгҖӮ
еҜ№дәҺжү©еј еҚ·з§ҜпјҢжҲ‘们еҹәжң¬дёҠеҸ–ж ёеҮҪж•°еңЁиҝӣиЎҢеҚ·з§Ҝиҝҗз®—д№ӢеүҚеңЁж ёеҮҪж•°зҡ„е…ғзҙ д№Ӣй—ҙеҠ дёҠй—ҙйҡ”гҖӮйҖҡиҝҮиҝҷж ·еҒҡпјҢеҶ…ж ёзҡ„жҺҘеҸ—еҢәеҹҹдјҡеўһеҠ пјҢиҖҢеҸӮж•°зҡ„ж•°йҮҸдјҡзӣёеҗҢгҖӮ
дёҺжҷ®йҖҡеҚ·з§ҜеұӮзӣёжҜ”пјҢе®ғзңӢиө·жқҘжҳҜиҝҷж ·зҡ„: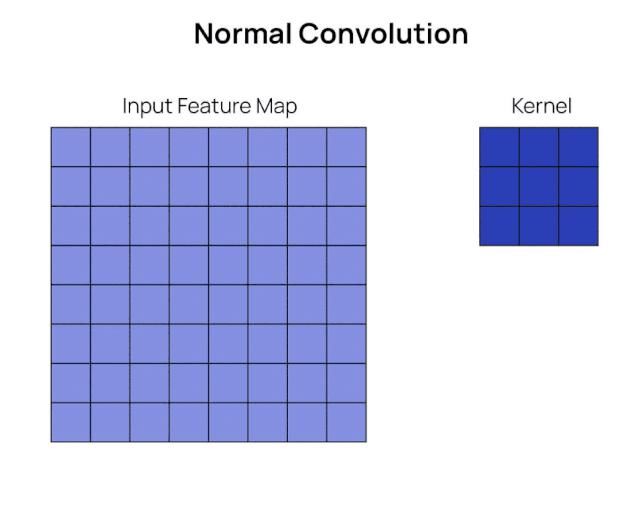
ж–Үз« еӣҫзүҮ
еҸҜд»ҘзңӢеҲ°пјҢеҶ…ж ёдёӯзҡ„е…ғзҙ ж•°йҮҸдҝқжҢҒдёҚеҸҳпјҢдҪҶжҳҜеә”з”ЁеҶ…ж ёзҡ„жңүж•Ҳйқўз§Ҝд»Һ3*3еўһеҠ еҲ°5*5гҖӮжҲ‘们иҝҳеҸҜд»Ҙж”№еҸҳж ёзҡ„иҶЁиғҖзҺҮпјҢиҝҷжң¬иҙЁдёҠж„Ҹе‘ізқҖж ёе…ғзҙ д№Ӣй—ҙзҡ„й—ҙйҡҷе°ҶжңүеӨҡе®ҪгҖӮеҜ№дәҺдёҠйқўдҫӢеӯҗдёӯзҡ„иҶЁиғҖж ёпјҢиҶЁиғҖзҺҮдёә2гҖӮй»ҳи®Өзҡ„еҚ·з§Ҝж ёзҡ„иҶЁиғҖзҺҮдёә1пјҢеҹәжң¬дёҠж„Ҹе‘ізқҖж ёе…ғзҙ д№Ӣй—ҙжІЎжңүй—ҙйҡҷгҖӮ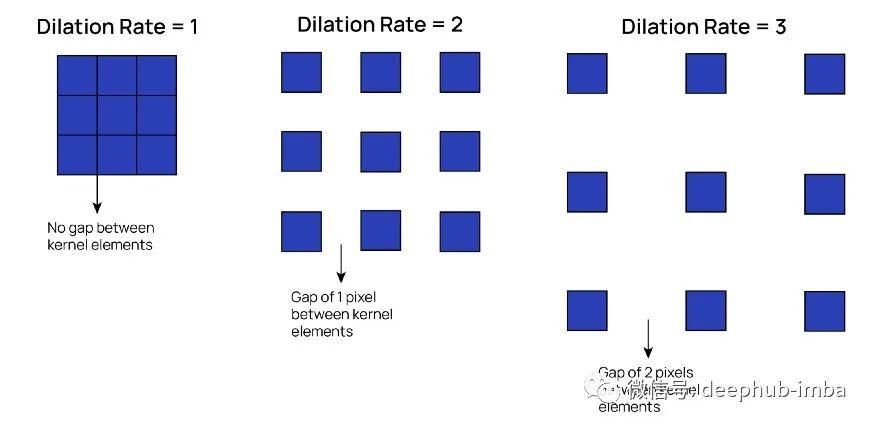
ж–Үз« еӣҫзүҮ
еҪ“жҲ‘们жғіи®©еҚ·з§Ҝеә”з”ЁдәҺжӣҙеӨ§зҡ„еҢәеҹҹпјҢеҗҢж—¶еҸҲиғҪиҠӮзңҒи®Ўз®—жҲҗжң¬ж—¶пјҢжҲ‘们е°ұдҪҝз”ЁдәҶжү©еј еҚ·з§ҜгҖӮеҰӮжһңжҲ‘们жғіз”ЁдёҖдёӘжҷ®йҖҡзҡ„еҚ·з§ҜеұӮиҰҶзӣ–5*5зҡ„йқўз§ҜпјҢйӮЈд№ҲжҲ‘们йңҖиҰҒдёҖдёӘ5*5йқўз§Ҝзҡ„ж ёпјҢд№ҹе°ұжҳҜ25дёӘе…ғзҙ гҖӮ然иҖҢпјҢеҰӮжһңжҲ‘们дҪҝз”Ёжү©еј зҺҮдёә2зҡ„жү©еј еҚ·з§ҜпјҢжҲ‘们еҸҜд»Ҙз”Ё9дёӘе…ғзҙ иҰҶзӣ–зӣёеҗҢзҡ„еҢәеҹҹгҖӮйҷӨжӯӨд№ӢеӨ–пјҢеҶ…ж ёзҡ„жҺҘеҸ—еҢәеҹҹд№ҹеўһеҠ дәҶпјҢдҪҝеҫ—е®ғ们иғҪеӨҹжҚ•жҚүеҲ°еңЁиҫ“е…Ҙзү№еҫҒеӣҫдёӯеҮәзҺ°зҡ„жӣҙз»Ҷзҡ„з»ҶиҠӮгҖӮ
еҲҶз»„еҚ·з§Ҝ
еңЁеҲҶз»„еҚ·з§ҜдёӯпјҢеҹәжң¬зҡ„жҰӮеҝөжҳҜжҲ‘们е°Ҷиҫ“е…Ҙдёӯзҡ„дҝЎйҒ“еҲҶжҲҗзӣёзӯүзҡ„з»„гҖӮ然еҗҺпјҢжҲ‘们е°ҶеҲҶй…ҚзӣёеҗҢж•°йҮҸзҡ„еҶ…ж ёз»ҷжҜҸдёҖз»„гҖӮжҜҸдёӘеҶ…ж ёе°ҶеҸӘеә”з”ЁдәҺе…¶еҗ„иҮӘз»„дёӯзҡ„йҖҡйҒ“пјҢиҖҢдёҚжҳҜеә”з”ЁдәҺиҫ“е…Ҙзҡ„жүҖжңүйҖҡйҒ“гҖӮ
дҫӢеҰӮпјҢеҰӮжһңжҲ‘们жңүдёҖдёӘжңү4дёӘйҖҡйҒ“зҡ„иҫ“е…Ҙзү№еҫҒеӣҫпјҢ并且жҲ‘们еёҢжңӣжҖ»е…ұжңү2з»„пјҢйӮЈд№ҲжҜҸз»„йғҪе°Ҷжңү2дёӘйҖҡйҒ“гҖӮеҒҮи®ҫжҜҸдёҖз»„жңү4дёӘеҶ…ж ёгҖӮжҜҸдёӘеҶ…ж ёзҡ„ж·ұеәҰе°Ҷдёә2пјҢеӣ дёәе®ғ们е°ҶеҸӘеә”з”ЁдәҺжҜҸдёӘз»„пјҢиҖҢдёҚжҳҜж•ҙдёӘиҫ“е…ҘгҖӮе°ҶдёӨз»„зҡ„иҫ“еҮәзү№еҫҒеӣҫиҝһжҺҘеңЁдёҖиө·пјҢеҪўжҲҗжңҖз»Ҳзҡ„иҫ“еҮәзү№еҫҒеӣҫгҖӮеӣ жӯӨпјҢеңЁжң¬дҫӢдёӯпјҢжҜҸз»„е°Ҷиҫ“еҮә4дёӘfeature mapпјҢеӣ жӯӨиҫ“еҮәзҡ„channelжҖ»ж•°дёә8гҖӮи®©жҲ‘们зңӢзңӢиҝҷдёӘдҫӢеӯҗзҡ„еҸҜи§ҶеҢ–и§ЈйҮҠ: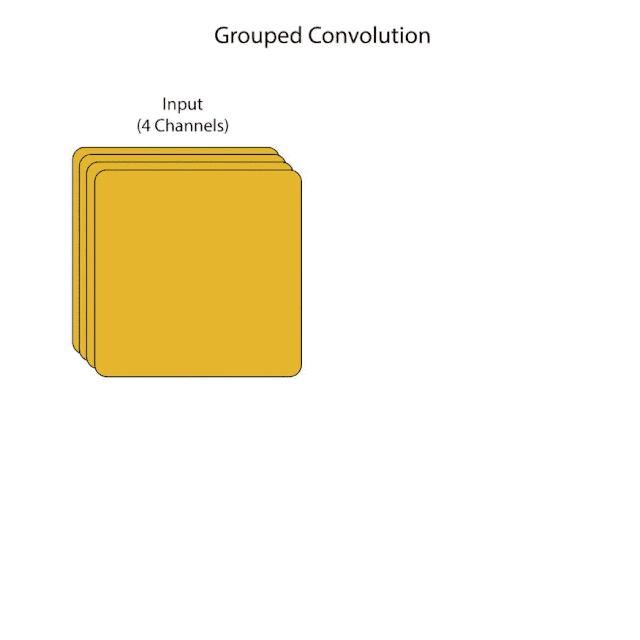
ж–Үз« еӣҫзүҮ
еҜ№дәҺеҲҶз»„еҚ·з§ҜпјҢжҲ‘们жң¬иҙЁдёҠжҳҜеңЁжҜҸдёҖеұӮ并иЎҢең°жү§иЎҢеҚ·з§ҜгҖӮиҝҷеўһеҠ дәҶжЁЎеһӢеңЁйҖҡиҝҮзҪ‘з»ңиҝӣиЎҢеҸҚеҗ‘дј ж’ӯж—¶еҸҜд»ҘйҮҮеҸ–зҡ„и·Ҝеҫ„ж•°йҮҸгҖӮйҷӨжӯӨд№ӢеӨ–пјҢе®ғиҝҳеҮҸе°‘дәҶиҜҘеұӮзҡ„и®Ўз®—жҲҗжң¬пјҢеӣ дёәжҜҸдёӘеҶ…ж ёе°ҶжӢҘжңүжӣҙе°‘зҡ„еҸӮж•°пјҢ并且е°Ҷеә”з”ЁдәҺиҫ“е…Ҙдёӯзҡ„жӣҙе°‘зҡ„йҖҡйҒ“гҖӮиҝҷе°ұжҳҜжҲ‘们дҪҝз”Ёз»„еҗҲеҚ·з§Ҝзҡ„еҺҹеӣ гҖӮиҝҷдәӣеңЁResNextжһ¶жһ„дёӯдҪҝз”ЁгҖӮ
дҪңиҖ…пјҡHarsha Bommana
deephubзҝ»иҜ‘з»„
DeepHub
жҺЁиҚҗйҳ…иҜ»
- жҙҫеҮәжүҖ|жі°е®үеёӮе…¬е®үеұҖеІұеІіеҲҶеұҖзҘқйҳіжҙҫеҮәжүҖж·ұе…ҘйӣҶеёӮејҖеұ•е®үе…ЁйҳІиҢғе®Јдј
- еҶңдёҡ科жҠҖзӨҫдјҡеҢ–жңҚеҠЎ|ж”ҝеәңеҠ ејәеҶңдёҡ科жҠҖзӨҫдјҡеҢ–жңҚеҠЎдҪ“зі»е»әи®ҫ 2020еҶңдёҡ科жҠҖиЎҢдёҡеёӮеңәж·ұеәҰеҲҶжһҗ
- жҷәиғҪ硬件|жӯҢе°”иӮЎд»Ҫж·ұеәҰи§ЈжһҗпјҡTWSиҖіжңәж”ҫйҮҸеј•йўҶеўһй•ҝпјҢзІҫеҜҶеҲ¶йҖ еҶ…еҠҹй“ёе°ұжҲҗй•ҝ
- е№ҝиҘҝиҙөжёҜжёҜеҚ—еҢәжЈҖеҜҹйҷўж·ұе…Ҙд№Ўжқ‘ејҖеұ•зҰҒжҜ’е®Јдј
- дёӯиҖҒе№ҙ|ж·ұеәҰпјҡдёӯиҖҒе№ҙиә«дҪ“жңәиғҪеҸҳеҢ–еӮ¬з”ҹж•°еҚғдәҝдёӯиҖҒе№ҙжңҚиЈ…еёӮеңәпјҒ
- е…үзјҶдә§йҮҸе…үзәӨе…үзјҶ|2020дёҠеҚҠе№ҙе…ЁеӣҪе…үзјҶдә§йҮҸ1.32дәҝиҠҜеҚғзұі 2020е…үзәӨе…үзјҶжқҗж–ҷиЎҢдёҡеёӮеңәж·ұеәҰеҲҶжһҗ
- ж•°еӯ—йҹід№җдёӯеӣҪйҹід№җеҚҺиҜӯж•°еӯ—йҹід№җ|2020е№ҙж•°еӯ—йҹід№җиЎҢдёҡеёӮеңәж·ұеәҰеҲҶжһҗ жҖ»дҪ“й”Җе”®йўқзӘҒз ҙ3дәҝе…ғеӨ§е…і
- и§Ҷйў‘еңЁзәҝи§Ҷйў‘зҪ‘з»ңи§Ҷйў‘|2020е№ҙеңЁзәҝи§Ҷйў‘иЎҢдёҡеёӮеңәж·ұеәҰеҲҶжһҗ зҪ‘з»ңи§Ҷйў‘зӣёе…ідјҒдёҡжіЁеҶҢйҮҸдёә4.2дёҮ家
- жҷәиғҪй—ЁзҰҒдәәи„ёиҜҶеҲ«жҷәж…§еҹҺеёӮ|2020жҷәиғҪй—ЁзҰҒиЎҢдёҡеёӮеңәеҸ‘еұ•и¶ӢеҠҝж·ұеәҰеҲҶжһҗ дәәи„ёиҜҶеҲ«жҲҗдёәжҷәиғҪй—ЁзҰҒдёҖеӨ§и¶ӢеҠҝ
- ж”»з•Ҙ|ж— ж·ұеәҰдёҚдә‘еҚ—вҖ”вҖ”дёҪжұҹе·ҙжӢүзҘһеұұеҫ’жӯҘз©ҝи¶Ҡж”»з•Ҙ



![[еқҰиЁҖ]收е…ҘжҸҗй«ҳдәҶпјҹж»ҙж»ҙеҸёжңәеқҰиЁҖпјҡеӣ дёәе№іеҸ°иҝҷжіўж“ҚдҪңпјҢзҺ°еңЁж”¶е…Ҙ](/renwen/images/defaultpic.gif)













