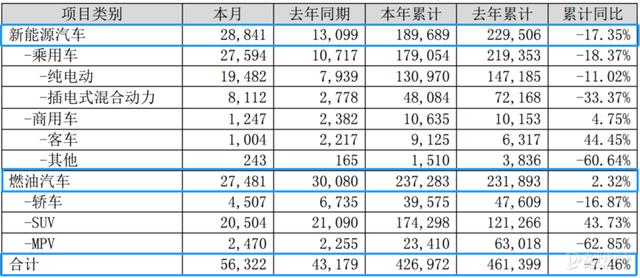
svm问题中拉格朗日对偶后的限制条件
基本型使用拉格朗日乘子法得到了SVM的拉格朗日函数。其对w求导等于0再带回就可以把w和b消掉，得到对偶型。另外拉格朗日函数对b求导也要等于0，于是得到了你说的第二个条件。
■网友
在拉格朗日对偶问题的推导过程中，由拉格朗日等式
经过推导可以将SVM对偶问题转化为无条件形式：
后面min的部分是对L(b,w,alpha)计算最小值，根据梯度下降法，最小值处的梯度=0。则分别对b，w求导可以得到：
也就是说我们最终求的最优解是同时满足上述两个条件的。这个时候我们的条件其实一共有三种，分别是：
我们最终将其带入到原等式，将b和w消掉。我们简化dual SVM的问题到只和alpha有关，而第三种约束条件表示的是alpha与w之间的关系，在求解对偶问题时，计算alpha的过程中不需要w，所以可以将第三个问题省略，只需要将前两种约束作为最优化求解的约束。
并且KKT条件并不是只保留了第二种约束。KKT条件是包含上述三种约束的。KKT条件一共有如下：
最后我们可以根据KKT条件，由alpha计算得到b，w。
■网友
不知道题主是不是想问为什么对b要求偏导数？
据我肤浅的理解，对b求导是必须的。
首先，对问题：在约束g(x)\u0026lt;=0（或=0）下，求f(x)的最小值。其拉格朗日乘子法得到对偶问题的几何意义就是得到：
入\u0026gt;=0
即：两个曲面的梯度线性相关。当然还得讨论不等式约束条件下，两个梯度的方向问题。
那么重点来了：
此处f(x)的真实表达式（在SVM的经典描述下）f(x)---\u0026gt;f(w, b) = 1/2*||w||^2；g(x) ----\u0026gt;g(w, b) = 1 - yi*(w^T*xi + b)\u0026lt;=0。两者的梯度为(w, 0)和(-yi*xi, -yi)，得到最终表达式：
(w, 0) + （对底数i求和）αi*(-yi*xi, -yi) = (0, 0)
这是一个二元函数求梯度的问题。
故：对b求偏导数是必须的。
【svm问题中拉格朗日对偶后的限制条件】 PS：没用公式编辑器，抱歉
推荐阅读
![[整机质量部]整机质量部四月份优秀员工-王奉军](https://imgcdn.toutiaoyule.com/20200502/20200502120602179272a_t.jpeg)
- 是不是只有知乎专栏的文章才能在话题中显示
- 求助关于libsvm的predict方法的具体意义
- 华为|华为在法国设立拉格朗日研发中心
- SVM(支持向量机)中的特征的值， 是数值型的还是离散型的
- 怎么样减少支持向量机（SVM）的训练时间
- 在模式识别中，怎样判断线性可分和非线性可分怎样选择SVM的类型
- C#,Java和Objective C都是啥?
- SVM算法采用高斯核函数，核函数的参数对结果影响大吗
- LIS 问题中怎样定义子状态
- 暗黑版西游记的作者是谁