函数|高考数学易考的62个高频考点！出题人再厉害也逃不开( 三 )

2020-09-21

文章图片

3
等价转化法
通过"化复杂为简单、化陌生为熟悉" ，将问题等价转化成便于解决的问题，从而得出正确的结果。
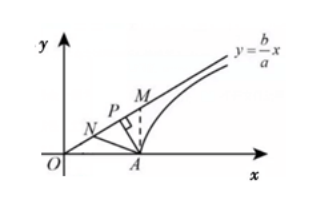
例题：不论K为任何实数，直线y=kx+1与直线x 2 +y 2 -2ax+a 2 -2a-4=0恒有交点，则实数a的取值范围为
解析：题设条件等价于点（0,1）在圆内或圆上，或等价与点（0,1）到圆（x-a） 2 +y 2 =2a+4,所以-1≤a≤3
注意事项
选择题、填空题在考试时都是只要结果，不看过程。因此，可以充分利用题干和选项提供的信息作出判断，先定性后定量，先特殊后推理，先间接后直接，先排除后求解，一定要小题巧解，避免小题大做，浪费太多时间在前面的小题上。

文章图片

通用答题套路
1
三角变换与三角函数的性质问题
①解题路线图

不同角化同角。
降幂扩角。
化f(x)＝Asin(ωx＋φ)＋h 。
结合性质求解。

②构建答题模板

化简：三角函数式的化简，一般化成y＝Asin(ωx＋φ)＋h的形式，即化为“一角、一次、一函数”的形式。
整体代换：将ωx＋φ看作一个整体，利用y＝sin x ， y＝cos x的性质确定条件。
求解：利用ωx＋φ的范围求条件解得函数y＝Asin(ωx＋φ)＋h的性质，写出结果。
反思：反思回顾，查看关键点，易错点，对结果进行估算，检查规范性。

2
解三角函数问题
①解题路线图

化简变形；用余弦定理转化为边的关系；变形证明。
用余弦定理表示角；用基本不等式求范围；确定角的取值范围。

②构建答题模板

定条件：即确定三角形中的已知和所求，在图形中标注出来，然后确定转化的方向。
定工具：即根据条件和所求，合理选择转化的工具，实施边角之间的互化。
求结果。
再反思：在实施边角互化的时候应注意转化的方向，一般有两种思路：一是全部转化为边之间的关系；二是全部转化为角之间的关系，然后进行恒等变形。

3
数列的通项、求和问题
①解题路线图

先求某一项，或者找到数列的关系式。
求通项公式。
求数列和通式。

②构建答题模板

找递推：根据已知条件确定数列相邻两项之间的关系，即找数列的递推公式。
求通项：根据数列递推公式转化为等差或等比数列求通项公式，或利用累加法或累乘法求通项公式。
定方法：根据数列表达式的结构特征确定求和方法(如公式法、裂项相消法、错位相减法、分组法等) 。
写步骤：规范写出求和步骤。
再反思：反思回顾，查看关键点、易错点及解题规范。

4
利用空间向量求角问题
①解题路线图

建立坐标系，并用坐标来表示向量。
空间向量的坐标运算。
用向量工具求空间的角和距离。

②构建答题模板

上一篇：范冰冰|刚传出与前男友复合，就立刻开始秀恩爱，“范爷”这波操作神了

下一篇：财经类|热门专业中的香饽饽：30所财经类热门院校及专业实力盘点！