з®—жі•иҗҢж–°еҰӮдҪ•еӯҰеҘҪеҠЁжҖҒ规еҲ’пјҲ3пјү( е…« )
и§ЈйўҳжҖқи·Ҝжң¬йўҳдёҺдёҠдёҖйўҳе”ҜдёҖзҡ„еҢәеҲ«еңЁдәҺ пјҢ дёҠдёҖйўҳиҰҒжұӮзҡ„гҖҢеҮ‘жҲҗжҖ»йҮ‘йўқжңҖе°‘йңҖиҰҒзҡ„зЎ¬еёҒдёӘж•°гҖҚ пјҢ иҖҢжң¬йўҳжұӮзҡ„жҳҜгҖҢеҮ‘жҲҗжҖ»йҮ‘йўқзҡ„ж–№жЎҲж•°гҖҚ гҖӮ еӣ жӯӨеҸӘйңҖзЁҚеҫ®ж”№еҠЁдёҖдёӢгҖҢDP зҠ¶жҖҒж„Ҹд№үгҖҚд»ҘеҸҠгҖҢDP иҪ¬з§»ж–№зЁӢгҖҚеҚіеҸҜ гҖӮ
з”ұдәҺжң¬йўҳзҡ„зЎ¬еёҒдҫқ然еҸҜд»Ҙж— йҷҗеҸ– пјҢ еӣ жӯӨд»Қ然дҪҝз”ЁгҖҢе®Ңе…ЁиғҢеҢ…гҖҚжЁЎеһӢиҝӣиЎҢжұӮи§Ј гҖӮ е®ҡд№ү
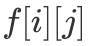 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
иЎЁзӨәд»…иҖғиҷ‘еүҚ i зұ»зЎ¬еёҒ пјҢ е…¶жҖ»йҮ‘йўқдёә j ж—¶зҡ„з»„еҗҲж•° гҖӮ еӣ жӯӨеҸҜд»Ҙеҫ—еҲ°еҰӮдёӢгҖҢDP иҪ¬з§»ж–№зЁӢгҖҚпјҡ
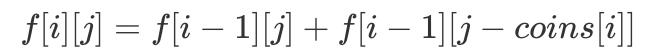 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
еҲқе§ӢжқЎд»¶дёә пјҢ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
гҖӮ жҺҘдёӢжқҘдҪҝз”ЁгҖҢе®Ңе…ЁиғҢеҢ…гҖҚж»ҡеҠЁж•°з»„зүҲжң¬зҡ„д»Јз ҒеҚіеҸҜ пјҢ е…·дҪ“з»ҶиҠӮеҰӮдёӢ гҖӮ
C++ д»Јз Ғе®һзҺ°class Solution {public:vector?474. дёҖе’Ңйӣ¶йўҳзӣ®жҸҸиҝ°еңЁи®Ўз®—жңәз•Ңдёӯ пјҢ жҲ‘们жҖ»жҳҜиҝҪжұӮз”Ёжңүйҷҗзҡ„иө„жәҗиҺ·еҸ–жңҖеӨ§зҡ„收зӣҠ гҖӮ
зҺ°еңЁ пјҢ еҒҮи®ҫдҪ еҲҶеҲ«ж”Ҝй…ҚзқҖ m дёӘ 0 е’Ң n дёӘ 1 гҖӮ еҸҰеӨ– пјҢ иҝҳжңүдёҖдёӘд»…еҢ…еҗ« 0 е’Ң 1 еӯ—з¬ҰдёІзҡ„ж•°з»„ гҖӮ
дҪ зҡ„д»»еҠЎжҳҜдҪҝз”Ёз»ҷе®ҡзҡ„ m дёӘ 0 е’Ң n дёӘ 1пјҢ жүҫеҲ°иғҪжӢјеҮәеӯҳеңЁдәҺж•°з»„дёӯзҡ„еӯ—з¬ҰдёІзҡ„жңҖеӨ§ж•°йҮҸ гҖӮ жҜҸдёӘ 0 е’Ң 1 иҮіеӨҡиў«дҪҝз”ЁдёҖж¬Ў гҖӮ
зӨәдҫӢ 1иҫ“е…Ҙ: Array = {"10", "0001", "111001", "1", "0"}, m = 5, n = 3иҫ“еҮә: 4?и§ЈйҮҠ: жҖ»е…ұ 4 дёӘеӯ—з¬ҰдёІеҸҜд»ҘйҖҡиҝҮ 5 дёӘ 0 е’Ң 3 дёӘ 1 жӢјеҮә пјҢ еҚі "10","0001","1","0" гҖӮ зӨәдҫӢ 2иҫ“е…Ҙ: Array = {"10", "0", "1"}, m = 1, n = 1?иҫ“еҮә: 2?и§ЈйҮҠ: дҪ еҸҜд»ҘжӢјеҮә "10" пјҢ дҪҶд№ӢеҗҺе°ұжІЎжңүеү©дҪҷж•°еӯ—дәҶ гҖӮ жӣҙеҘҪзҡ„йҖүжӢ©жҳҜжӢјеҮә "0" е’Ң "1" гҖӮ жҸҗзӨә
- з»ҷе®ҡ 0 е’Ң 1 зҡ„ж•°йҮҸйғҪдёҚдјҡи¶…иҝҮ 100 гҖӮ
- з»ҷе®ҡеӯ—з¬ҰдёІж•°з»„зҡ„й•ҝеәҰдёҚдјҡи¶…иҝҮ 600 гҖӮ
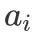 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫдёӘ 0 пјҢ
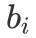 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫдёӘ 1 пјҢ зҺ°й—®жңҖеӨҡеҸҜд»ҘжӢјеҮәеӨҡе°‘дёӘеӯ—з¬ҰдёІ гҖӮ
иҝҷдёӘйўҳзңӢдјјеҸҜиғҪе’ҢиғҢеҢ…жІЎеӨӘеӨ§е…ізі» пјҢ дҪҶд»”з»ҶжҖқиҖғд№ӢеҗҺ пјҢ иҝҳжҳҜеҸҜд»ҘеҸ‘зҺ°жӯӨйўҳзҡ„жң¬иҙЁд»Қ然жҳҜйҖүеҸ–иӢҘе№ІдёӘеӯ—з¬ҰдёІ пјҢ дҪҝе…¶ 0 е’Ң 1 зҡ„дёӘж•°д№Ӣе’ҢеҲҶеҲ«е°ҸдәҺзӯүдәҺ m е’Ң n пјҢ еӣ жӯӨд»Қ然жҳҜдёҖйҒ“иғҢеҢ…й—®йўҳ гҖӮ 并且з”ұдәҺжҜҸдёҖдёӘеӯ—з¬ҰдёІеҸӘиғҪйҖүдёҖж¬Ў пјҢ еӣ жӯӨжҳҜдёҖйҒ“гҖҢ0/1 иғҢеҢ…гҖҚй—®йўҳ гҖӮ
жҲ‘们д»ҝз…§гҖҢ0/1 иғҢеҢ…гҖҚзҡ„жҖқи·Ҝ пјҢ е®ҡд№ү
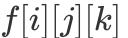 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫиЎЁзӨәеҜ№дәҺеүҚ i дёӘеӯ—з¬ҰдёІ пјҢ дёҖе…ұжңү j дёӘ 0 е’Ң k дёӘ 1 ж—¶ пјҢ иғҪжӢјеҮәзҡ„жңҖеӨ§еӯ—з¬ҰдёІдёӘж•° гҖӮ
еҸҜд»ҘеҸ‘зҺ°еҜ№жҜ”гҖҢ0/1 иғҢеҢ…гҖҚзҡ„еҹәзЎҖжЁЎеһӢ пјҢ жҲ‘们е°ҶгҖҢDP зҠ¶жҖҒгҖҚд»ҺдәҢз»ҙжү©еұ•еҲ°дәҶдёүз»ҙ пјҢ дё»иҰҒеҺҹеӣ еңЁдәҺжң¬йўҳжңүдёӨдёӘеҸӮж•° пјҢ еҲҶеҲ«жҳҜ 0 е’Ң 1 зҡ„дёӘж•° гҖӮ еҸҜд»ҘзҗҶи§ЈдёәжңүдёӨдёӘиғҢеҢ… пјҢ иҰҒиЈ…дёӨз§ҚдёңиҘҝ пјҢ дҪҶжң¬иҙЁдёҚеҸҳ пјҢ еҸӘйңҖеңЁеҺҹе…ҲеҹәзЎҖдёҠжү©еұ•дёҖз»ҙеҚіеҸҜ гҖӮ
еӣ жӯӨжҲ‘们еҸҜд»Ҙд»ҝз…§еҺҹе…Ҳзҡ„еҹәзЎҖжЁЎеһӢ пјҢ еҫ—еҲ°еҰӮдёӢгҖҢDP иҪ¬з§»ж–№зЁӢгҖҚпјҡ
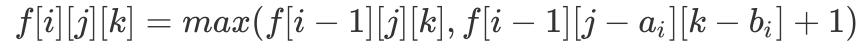 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫеҲқе§ӢжқЎд»¶дёә
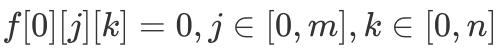 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫгҖӮ з”ұдәҺжң¬йўҳеҸӘжҳҜеңЁгҖҢ0/1 иғҢеҢ…гҖҚжЁЎеһӢеҹәзЎҖдёҠжү©еұ•дәҶдёҖз»ҙ пјҢ еӣ жӯӨжҲ‘们д»Қ然еҸҜд»ҘдҪҝз”ЁгҖҢж»ҡеҠЁж•°з»„гҖҚзҡ„ж–№жі•е°Ҷдёүз»ҙз©әй—ҙйҷҚдҪҺиҮідәҢз»ҙз©әй—ҙ пјҢ е…·дҪ“д»Јз ҒеҰӮдёӢжүҖзӨә гҖӮ
жҺЁиҚҗйҳ…иҜ»
- еӨ§дёҖйқһи®Ўз®—жңәдё“дёҡзҡ„еӯҰз”ҹпјҢеҰӮдҪ•еҲ©з”ЁеҜ’еҒҮиҮӘеӯҰCиҜӯиЁҖ
- еҗ‘ж—Ҙи‘өиҝңзЁӢжҺ§еҲ¶дјҒдёҡзүҲе®ўжҲ·з«Ҝжӣҙж–°еҚҮзә§пјҢдјҳеҢ–иҝңжҺ§UIйҖӮй…ҚSADDCеҶ…ж ёз®—жі•
- зәўзұіK40жёІжҹ“еӣҫжӣқе…үпјҡеұ…дёӯжҢ–еӯ”+еҗҺзҪ®еӣӣж‘„пјҢиҝҷеӨ–и§ӮдҪ и§үеҫ—еҰӮдҪ•пјҹ
- еҘӢж–—|иҜҘеҰӮдҪ•зңӢеҫ…жӢјеӨҡеӨҡе‘ҳе·ҘзҢқжӯ»пјҡйј“еҠұеҘӢж–—пјҢд№ҹиҰҒдҝқжҠӨеҘҪеҘӢж–—иҖ…
- иЈ…жңәзӮ№дёҚдә® еҰӮдҪ•з®Җжҳ“жҺ’жҹҘ硬件问йўҳпјҹ
- иҷҫзұійҹід№җе®Јеёғе…іеҒңпјҒжҲ‘зҡ„жӯҢеҚ•еҰӮдҪ•еҜје…ҘQQйҹід№җгҖҒзҪ‘жҳ“дә‘йҹід№җпјҹ
- дәәи„ёиҜҶеҲ«и®ҫеӨҮдё»жқҝеҰӮдҪ•йҖүеһӢ иҪҜзЎ¬ж•ҙеҗҲеӨ§е№…зј©зҹӯејҖеҸ‘ж—¶й—ҙ
- Mini-LEDдә§е“Ғж•Ҳжһң究з«ҹеҰӮдҪ•пјҹ
- 专家д»Ӣз»ҚеҰӮдҪ•еҲӨж–ӯжҷәиғҪжүӢжңәиў«е…ҘдҫөпјҡиҝҗиЎҢйҖҹеәҰеҸҳж…ўгҖҒз”өжұ ж¶ҲиҖ—иҝҮеҝ«д»ҘеҸҠеҚЎйЎҝ
- еңЁи°·жӯҢз®—жі•жӣҙж–°д№ӢеҗҺ2020е№ҙзӣ—зүҲзҪ‘з«ҷжөҒйҮҸй”җеҮҸдёүеҲҶд№ӢдёҖ




















