з®—жі•иҗҢж–°еҰӮдҪ•еӯҰеҘҪеҠЁжҖҒ规еҲ’пјҲ3пјү( дә” )
еӣ жӯӨеҜ№дәҺ第 i зұ»зү©е“Ғ пјҢ е…¶дёӘж•°дёә
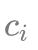 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҢ жҲ‘们еҸҜд»ҘжұӮеҮәж»Ўи¶і
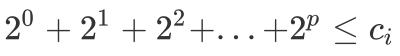 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
зҡ„жңҖеӨ§зҡ„ p пјҢ 并д»Ө
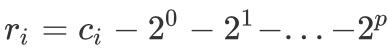 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
гҖӮ
еӣ дёә p жҳҜжңҖеӨ§зҡ„ пјҢ жүҖд»Ҙ
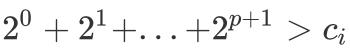 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҢ еҚі
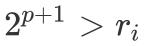 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
гҖӮ еҸҲеӣ дёә
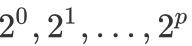 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
зҡ„жңҖеӨ§иЎЁзӨәиҢғеӣҙдёә
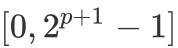 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҢ еӣ жӯӨжҲ‘们еҸҜд»Ҙд»Һ
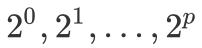 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
дёӯйҖүеҸ–иӢҘе№ІдёӘж•°иЎЁзӨәеҮә
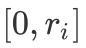 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
дёӯзҡ„д»»дҪ•ж•ҙж•° гҖӮ
еҸҲеӣ дёә
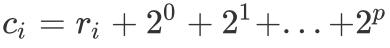 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҢ еӣ жӯӨжҲ‘们еҸҜд»ҘдҪҝз”Ё
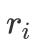 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
д»ҘеҸҠ
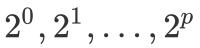 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
иЎЁзӨәеҮә
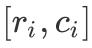 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
дёӯзҡ„д»»дҪ•ж•ҙж•° гҖӮ
жүҖд»Ҙ
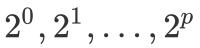 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҢ
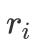 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
зҡ„иЎЁзӨәиҢғеӣҙжҒ°еҘҪдёә
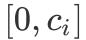 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҢ еҚіжҲ‘们еҸҜд»Ҙе°Ҷж•°йҮҸдёә
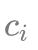 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
зҡ„第 i зұ»зү©е“ҒжӢҶеҲҶдёә p + 2 дёӘзү©е“Ғ пјҢ е…¶дҪ“з§ҜеҲҶеҲ«дёәпјҡ
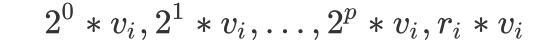 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
е…¶д»·еҖјеҲҶеҲ«дёәпјҡ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
жӢҶеҲҶе®ҢжҜҸдёҖзұ»зү©е“ҒеҗҺ пјҢ жҲ‘们еҶҚдҪҝз”ЁгҖҢ0/1 иғҢеҢ…гҖҚжЁЎеһӢеҚіеҸҜжұӮеҮәзӯ”жЎҲ пјҢ жҖ»ж—¶й—ҙеӨҚжқӮеәҰдёә
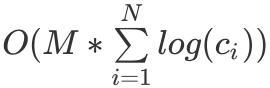 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
иғҢеҢ…й—®йўҳзү№зӮ№иҮіжӯӨжҲ‘们д»Ӣз»Қе®ҢдәҶдёүеӨ§еёёи§Ғзҡ„иғҢеҢ…жЁЎеһӢ пјҢ еҲҶеҲ«жҳҜгҖҢ0/1 иғҢеҢ…гҖҚгҖҒгҖҢе®Ңе…ЁиғҢеҢ…гҖҚгҖҒгҖҢеӨҡйҮҚиғҢеҢ…гҖҚ пјҢ е…¶еҢәеҲ«д»…д»…еңЁдәҺжҜҸдёҖзұ»зү©е“ҒеҸҜд»ҘйҖүеӨҡе°‘дёӘ гҖӮ е…¶дёӯгҖҢ0/1 иғҢеҢ…гҖҚжҳҜжҜҸдёҖзұ»зү©е“ҒеҸӘиғҪйҖүдёҖдёӘ пјҢ гҖҢе®Ңе…ЁиғҢеҢ…гҖҚеҲҷжҳҜжҜҸдёҖзұ»зү©е“ҒеҸҜд»ҘйҖүж— ж•°дёӘ пјҢ иҖҢгҖҢеӨҡйҮҚиғҢеҢ…гҖҚеҲҷжҳҜ第 i зұ»зү©е“ҒжңҖеӨҡеҸҜд»ҘйҖү
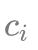 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
дёӘ гҖӮ
еӣ жӯӨжҲ‘们еҸҜд»ҘеҪ’зәігҖҢиғҢеҢ…й—®йўҳгҖҚзҡ„зү№зӮ№пјҡжңү N зұ»зү©е“Ғ пјҢ жҜҸзұ»зү©е“ҒеҸҜд»ҘйҖү 1 дёӘгҖҒж— ж•°дёӘжҲ–
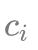 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
жҺЁиҚҗйҳ…иҜ»
- еӨ§дёҖйқһи®Ўз®—жңәдё“дёҡзҡ„еӯҰз”ҹпјҢеҰӮдҪ•еҲ©з”ЁеҜ’еҒҮиҮӘеӯҰCиҜӯиЁҖ
- еҗ‘ж—Ҙи‘өиҝңзЁӢжҺ§еҲ¶дјҒдёҡзүҲе®ўжҲ·з«Ҝжӣҙж–°еҚҮзә§пјҢдјҳеҢ–иҝңжҺ§UIйҖӮй…ҚSADDCеҶ…ж ёз®—жі•
- зәўзұіK40жёІжҹ“еӣҫжӣқе…үпјҡеұ…дёӯжҢ–еӯ”+еҗҺзҪ®еӣӣж‘„пјҢиҝҷеӨ–и§ӮдҪ и§үеҫ—еҰӮдҪ•пјҹ
- еҘӢж–—|иҜҘеҰӮдҪ•зңӢеҫ…жӢјеӨҡеӨҡе‘ҳе·ҘзҢқжӯ»пјҡйј“еҠұеҘӢж–—пјҢд№ҹиҰҒдҝқжҠӨеҘҪеҘӢж–—иҖ…
- иЈ…жңәзӮ№дёҚдә® еҰӮдҪ•з®Җжҳ“жҺ’жҹҘ硬件问йўҳпјҹ
- иҷҫзұійҹід№җе®Јеёғе…іеҒңпјҒжҲ‘зҡ„жӯҢеҚ•еҰӮдҪ•еҜје…ҘQQйҹід№җгҖҒзҪ‘жҳ“дә‘йҹід№җпјҹ
- дәәи„ёиҜҶеҲ«и®ҫеӨҮдё»жқҝеҰӮдҪ•йҖүеһӢ иҪҜзЎ¬ж•ҙеҗҲеӨ§е№…зј©зҹӯејҖеҸ‘ж—¶й—ҙ
- Mini-LEDдә§е“Ғж•Ҳжһң究з«ҹеҰӮдҪ•пјҹ
- 专家д»Ӣз»ҚеҰӮдҪ•еҲӨж–ӯжҷәиғҪжүӢжңәиў«е…ҘдҫөпјҡиҝҗиЎҢйҖҹеәҰеҸҳж…ўгҖҒз”өжұ ж¶ҲиҖ—иҝҮеҝ«д»ҘеҸҠеҚЎйЎҝ
- еңЁи°·жӯҢз®—жі•жӣҙж–°д№ӢеҗҺ2020е№ҙзӣ—зүҲзҪ‘з«ҷжөҒйҮҸй”җеҮҸдёүеҲҶд№ӢдёҖ












