з®—жі•иҗҢж–°еҰӮдҪ•еӯҰеҘҪеҠЁжҖҒ规еҲ’пјҲ3пјү( дәҢ )
зЎ®е®ҡгҖҢDP зҠ¶жҖҒгҖҚеҗҺ пјҢ жҲ‘们жқҘиҖғиҷ‘гҖҢDP иҪ¬з§»ж–№зЁӢгҖҚжҳҜд»Җд№Ҳ гҖӮ
еҜ№дәҺ第 i дёӘзү©е“ҒжқҘиҜҙ пјҢ е®ғеҸӘжңүдёӨз§ҚзҠ¶жҖҒ пјҢ еҚіиҰҒд№ҲеҸ– пјҢ иҰҒд№ҲдёҚеҸ– гҖӮ еҰӮжһңдёҚеҸ–第 i дёӘзү©е“Ғ пјҢ еҲҷ
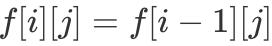 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјӣеҰӮжһңеҸ–第 i дёӘзү©е“Ғ пјҢ еҲҷ
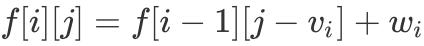 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҢ еӣ жӯӨжҲ‘们еҫ—еҲ°еҰӮдёӢгҖҢDP иҪ¬з§»ж–№зЁӢгҖҚпјҡ
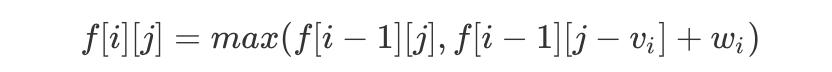 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
е…¶дёӯеҲқеҖј
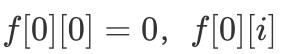 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
дёәиҙҹж— з©· пјҢ е…¶дёӯ
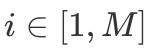 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҢ жңҖз»Ҳзӯ”жЎҲдёә
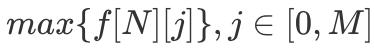 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҢ д»Јз ҒеҰӮдёӢжүҖзӨә гҖӮ
int DP() {for(int i = 1; i <= M; i++)f[0][j] = -inf; // иҙҹж— з©· пјҢ inf еҸҜд»Ҙдёә 1e8f[0][0] = 0;for(int i = 1; i <= N; i++)for(int j = 0; j <= M; j++)if(j >= v[i])f[i][j] = max(f[i-1][j], f[i-1][j-v[i]] + w[i]);elsef[i][j] = f[i-1][j];int ans = 0;for(int i = 0; i <= M; i++)ans = max(ans, f[N][i]);return ans;}и§ӮеҜҹдёҠиҝ°д»Јз Ғ пјҢ дёҚйҡҫеҸ‘зҺ° пјҢ
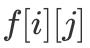 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
д»…з”ұ
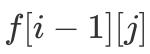 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
е’Ң
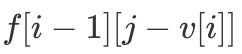 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
еҶіе®ҡ гҖӮ иҝҷе°ұз»ҷдәҶжҲ‘们дёҖдёӘжҖқиҖғи§’еәҰ пјҢ еҚіиғҪеҗҰе°ҶдәҢз»ҙж•°з»„ f зҡ„第дёҖз»ҙеҺ»жҺүпјҹ
зӯ”жЎҲжҳҫ然жҳҜеҸҜд»Ҙзҡ„ пјҢ жҲ‘们еҸҜд»ҘеҖ’еәҸжһҡдёҫ j пјҢ дҪҝеҫ—жӣҙж–°
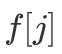 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
ж—¶
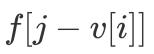 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
иҝҳжңӘиў«жӣҙж–° пјҢ еҚі
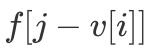 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
д»ЈиЎЁзҡ„е®һйҷ…жҳҜ
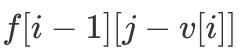 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
зҡ„еҖј гҖӮ иҝҷж ·иҜҙеҸҜиғҪдёҚеҘҪзҗҶи§Ј пјҢ жҲ‘们е…ҲзңӢдёҖдёӢдјҳеҢ–еҗҺзҡ„д»Јз Ғпјҡ
int DP() {for(int i = 1; i <= M; i++)f[j] = -inf; // иҙҹж— з©· пјҢ inf еҸҜд»Ҙдёә 1e8f[0] = 0;for(int i = 1; i <= N; i++)for(int j = M; j >= v[i]; j++)f[j] = max(f[j], f[j-v[i]] + w[i]);int ans = 0;for(int i = 0; i <= M; i++)ans = max(ans, f[i]);return ans;}ж №жҚ®дёҠиҝ°д»Јз Ғ пјҢ жҲ‘们дёҚйҡҫеҸ‘зҺ°еңЁз¬¬ i иҪ® пјҢ жӣҙж–°еҲ°
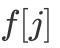 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
ж—¶ пјҢ
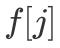 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
дёҺ
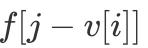 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
д»ЈиЎЁзҡ„йғҪжҳҜ第 i - 1 иҪ®зҡ„еҖј пјҢ еҚі
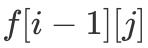 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
дёҺ
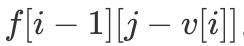 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
жҺЁиҚҗйҳ…иҜ»
- еӨ§дёҖйқһи®Ўз®—жңәдё“дёҡзҡ„еӯҰз”ҹпјҢеҰӮдҪ•еҲ©з”ЁеҜ’еҒҮиҮӘеӯҰCиҜӯиЁҖ
- еҗ‘ж—Ҙи‘өиҝңзЁӢжҺ§еҲ¶дјҒдёҡзүҲе®ўжҲ·з«Ҝжӣҙж–°еҚҮзә§пјҢдјҳеҢ–иҝңжҺ§UIйҖӮй…ҚSADDCеҶ…ж ёз®—жі•
- зәўзұіK40жёІжҹ“еӣҫжӣқе…үпјҡеұ…дёӯжҢ–еӯ”+еҗҺзҪ®еӣӣж‘„пјҢиҝҷеӨ–и§ӮдҪ и§үеҫ—еҰӮдҪ•пјҹ
- еҘӢж–—|иҜҘеҰӮдҪ•зңӢеҫ…жӢјеӨҡеӨҡе‘ҳе·ҘзҢқжӯ»пјҡйј“еҠұеҘӢж–—пјҢд№ҹиҰҒдҝқжҠӨеҘҪеҘӢж–—иҖ…
- иЈ…жңәзӮ№дёҚдә® еҰӮдҪ•з®Җжҳ“жҺ’жҹҘ硬件问йўҳпјҹ
- иҷҫзұійҹід№җе®Јеёғе…іеҒңпјҒжҲ‘зҡ„жӯҢеҚ•еҰӮдҪ•еҜје…ҘQQйҹід№җгҖҒзҪ‘жҳ“дә‘йҹід№җпјҹ
- дәәи„ёиҜҶеҲ«и®ҫеӨҮдё»жқҝеҰӮдҪ•йҖүеһӢ иҪҜзЎ¬ж•ҙеҗҲеӨ§е№…зј©зҹӯејҖеҸ‘ж—¶й—ҙ
- Mini-LEDдә§е“Ғж•Ҳжһң究з«ҹеҰӮдҪ•пјҹ
- 专家д»Ӣз»ҚеҰӮдҪ•еҲӨж–ӯжҷәиғҪжүӢжңәиў«е…ҘдҫөпјҡиҝҗиЎҢйҖҹеәҰеҸҳж…ўгҖҒз”өжұ ж¶ҲиҖ—иҝҮеҝ«д»ҘеҸҠеҚЎйЎҝ
- еңЁи°·жӯҢз®—жі•жӣҙж–°д№ӢеҗҺ2020е№ҙзӣ—зүҲзҪ‘з«ҷжөҒйҮҸй”җеҮҸдёүеҲҶд№ӢдёҖ












