з®—жі•иҗҢж–°еҰӮдҪ•еӯҰеҘҪеҠЁжҖҒ规еҲ’пјҲ3пјү( дёғ )
еӣ жӯӨй—®йўҳиҪ¬еҸҳдёәд»Һ N дёӘж•°дёӯйҖүеҸ–иӢҘе№ІдёӘж•° пјҢ дҪҝе…¶жҖ»е’Ңдёә
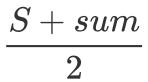 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҢ й—®жңүеӨҡе°‘з§ҚйҖүж•°ж–№жЎҲ гҖӮ
з”ұдәҺжҜҸдёӘж•°еҸӘиғҪйҖүдёҖж¬Ў пјҢ еӣ жӯӨжҲ‘们еҸҜд»Ҙиҫғдёәе®№жҳ“ең°е°ҶиҜҘй—®йўҳиҪ¬еҢ–дёәгҖҢ0/1 иғҢеҢ…гҖҚжЁЎеһӢ гҖӮ д»ҝз…§гҖҢ0/1 иғҢеҢ…гҖҚ пјҢ е®ҡд№ү
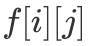 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
иЎЁзӨәд»…иҖғиҷ‘еүҚ i дёӘж•° пјҢ жңүеӨҡе°‘з§ҚйҖүж•°ж–№жЎҲдҪҝе…¶ж•°еӯ—е’Ңдёә j гҖӮ
еӣ жӯӨжҲ‘们еҸҜд»Ҙеҫ—еҲ°еҰӮдёӢгҖҢDP иҪ¬з§»ж–№зЁӢгҖҚпјҡ
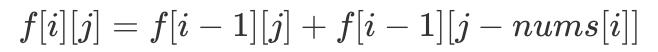 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
е®ҡд№үдёҖдёӢеҲқе§ӢжқЎд»¶ пјҢ
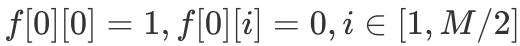 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
гҖӮ жҺҘдёӢжқҘзӣҙжҺҘеҘ—з”ЁгҖҢ0/1 иғҢеҢ…гҖҚж»ҡеҠЁж•°з»„зүҲжң¬зҡ„д»Јз ҒеҚіеҸҜ пјҢ е…·дҪ“з»ҶиҠӮи§ҒдёӢиҝ°д»Јз Ғ гҖӮ
C++ д»Јз Ғе®һзҺ°class Solution {public:vector322. йӣ¶й’ұе…‘жҚў?йўҳзӣ®жҸҸиҝ°з»ҷе®ҡдёҚеҗҢйқўйўқзҡ„зЎ¬еёҒ coins е’ҢдёҖдёӘжҖ»йҮ‘йўқ amount гҖӮ зј–еҶҷдёҖдёӘеҮҪж•°жқҘи®Ўз®—еҸҜд»ҘеҮ‘жҲҗжҖ»йҮ‘йўқжүҖйңҖзҡ„жңҖе°‘зҡ„зЎ¬еёҒдёӘж•° гҖӮ еҰӮжһңжІЎжңүд»»дҪ•дёҖз§ҚзЎ¬еёҒз»„еҗҲиғҪз»„жҲҗжҖ»йҮ‘йўқ пјҢ иҝ”еӣһ - 1 гҖӮ
зӨәдҫӢ 1иҫ“е…Ҙ: coins = [1, 2, 5], amount = 11иҫ“еҮә: 3 и§ЈйҮҠ: 11 = 5 + 5 + 1зӨәдҫӢ 2иҫ“е…Ҙ: coins = [2], amount = 3иҫ“еҮә: -1?жҸҗзӨә
- дҪ еҸҜд»Ҙи®ӨдёәжҜҸз§ҚзЎ¬еёҒзҡ„ж•°йҮҸжҳҜж— йҷҗзҡ„ гҖӮ
д»ҝз…§гҖҢе®Ңе…ЁиғҢеҢ…гҖҚзҡ„жҖқи·Ҝ пјҢ е®ҡд№ү
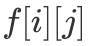 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫиЎЁзӨәд»…иҖғиҷ‘еүҚ i зұ»зЎ¬еёҒ пјҢ е…¶жҖ»йҮ‘йўқдёә j ж—¶жңҖе°‘жүҖйңҖзЎ¬еёҒдёӘж•° гҖӮ
еӣ жӯӨжҲ‘们еҸҜд»Ҙеҫ—еҲ°еҰӮдёӢгҖҢDP иҪ¬з§»ж–№зЁӢгҖҚпјҡ
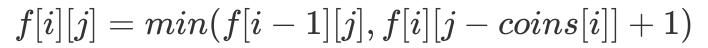 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫе®ҡд№үдёҖдёӢеҲқе§ӢжқЎд»¶ пјҢ
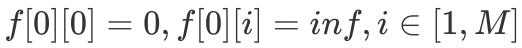 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫгҖӮ жҺҘдёӢжқҘзӣҙжҺҘеҘ—з”ЁгҖҢе®Ңе…ЁиғҢеҢ…гҖҚж»ҡеҠЁж•°з»„зүҲжң¬зҡ„д»Јз ҒеҚіеҸҜ пјҢ е…·дҪ“з»ҶиҠӮи§ҒдёӢиҝ°д»Јз Ғ гҖӮ
C++ д»Јз Ғе®һзҺ°
class Solution {public:vector f;const int inf = 1e8;int coinChange(vectorf[0] = 0;for(int i = 0; i < coins.size(); i++)for(int j = coins[i]; j <= amount; j++)f[j] = min(f[j], f[j-coins[i]] + 1);if(f[amount] == inf) return -1;else return f[amount];}}; ?518. йӣ¶й’ұе…‘жҚў IIйўҳзӣ®жҸҸиҝ°з»ҷе®ҡдёҚеҗҢйқўйўқзҡ„зЎ¬еёҒе’ҢдёҖдёӘжҖ»йҮ‘йўқ гҖӮ еҶҷеҮәеҮҪж•°жқҘи®Ўз®—еҸҜд»ҘеҮ‘жҲҗжҖ»йҮ‘йўқзҡ„зЎ¬еёҒз»„еҗҲж•° гҖӮ еҒҮи®ҫжҜҸдёҖз§Қйқўйўқзҡ„зЎ¬еёҒжңүж— йҷҗдёӘ гҖӮзӨәдҫӢ 1
иҫ“е…Ҙ: amount = 5, coins = [1, 2, 5]иҫ“еҮә: 4и§ЈйҮҠ: жңүеӣӣз§Қж–№ејҸеҸҜд»ҘеҮ‘жҲҗжҖ»йҮ‘йўқ:5=55=2+2+1?5=2+1+1+15=1+1+1+1+1зӨәдҫӢ 2иҫ“е…Ҙ: amount = 3, coins = [2]иҫ“еҮә: 0и§ЈйҮҠ: еҸӘз”Ёйқўйўқ2зҡ„зЎ¬еёҒдёҚиғҪеҮ‘жҲҗжҖ»йҮ‘йўқ3 гҖӮ ?зӨәдҫӢ 3иҫ“е…Ҙ: amount = 10, coins = [10] иҫ“еҮә: 1?жҸҗзӨә ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
жҺЁиҚҗйҳ…иҜ»
- еӨ§дёҖйқһи®Ўз®—жңәдё“дёҡзҡ„еӯҰз”ҹпјҢеҰӮдҪ•еҲ©з”ЁеҜ’еҒҮиҮӘеӯҰCиҜӯиЁҖ
- еҗ‘ж—Ҙи‘өиҝңзЁӢжҺ§еҲ¶дјҒдёҡзүҲе®ўжҲ·з«Ҝжӣҙж–°еҚҮзә§пјҢдјҳеҢ–иҝңжҺ§UIйҖӮй…ҚSADDCеҶ…ж ёз®—жі•
- зәўзұіK40жёІжҹ“еӣҫжӣқе…үпјҡеұ…дёӯжҢ–еӯ”+еҗҺзҪ®еӣӣж‘„пјҢиҝҷеӨ–и§ӮдҪ и§үеҫ—еҰӮдҪ•пјҹ
- еҘӢж–—|иҜҘеҰӮдҪ•зңӢеҫ…жӢјеӨҡеӨҡе‘ҳе·ҘзҢқжӯ»пјҡйј“еҠұеҘӢж–—пјҢд№ҹиҰҒдҝқжҠӨеҘҪеҘӢж–—иҖ…
- иЈ…жңәзӮ№дёҚдә® еҰӮдҪ•з®Җжҳ“жҺ’жҹҘ硬件问йўҳпјҹ
- иҷҫзұійҹід№җе®Јеёғе…іеҒңпјҒжҲ‘зҡ„жӯҢеҚ•еҰӮдҪ•еҜје…ҘQQйҹід№җгҖҒзҪ‘жҳ“дә‘йҹід№җпјҹ
- дәәи„ёиҜҶеҲ«и®ҫеӨҮдё»жқҝеҰӮдҪ•йҖүеһӢ иҪҜзЎ¬ж•ҙеҗҲеӨ§е№…зј©зҹӯејҖеҸ‘ж—¶й—ҙ
- Mini-LEDдә§е“Ғж•Ҳжһң究з«ҹеҰӮдҪ•пјҹ
- 专家д»Ӣз»ҚеҰӮдҪ•еҲӨж–ӯжҷәиғҪжүӢжңәиў«е…ҘдҫөпјҡиҝҗиЎҢйҖҹеәҰеҸҳж…ўгҖҒз”өжұ ж¶ҲиҖ—иҝҮеҝ«д»ҘеҸҠеҚЎйЎҝ
- еңЁи°·жӯҢз®—жі•жӣҙж–°д№ӢеҗҺ2020е№ҙзӣ—зүҲзҪ‘з«ҷжөҒйҮҸй”җеҮҸдёүеҲҶд№ӢдёҖ












