жҷәиғҪиҪҰз”өж„ҹе·®жҜ”е’Ңе·®еҠ жқғз®—жі•з ”з©¶( дёү )
в–І еӣҫC2.2.2 е…ҘејҜдёӯжңҹз®—жі•жҜ”иҫғ
з”ұеӣҫ2.2.1 пјҢ 2.2.2еҸҜд»ҘзңӢеҮә пјҢ е°ҸиҪҰеҲҡеҲҡе…ҘејҜ пјҢ иҷҪ然差жҜ”е’Ңе·®з®—жі•жүҖеёҰжқҘзҡ„иҫ“еҮәиҜҜе·®жӣІзәҝзҡ„ж–ңзҺҮиҫғй«ҳ пјҢ дҪҶжҳҜдёӨжӣІзәҝд№Ӣй—ҙжІЎжңүжҳҺжҳҫзҡ„еҢәеҲ« гҖӮ е°ҸиҪҰеҲқжӯҘиҝӣе…ҘејҜйҒ“еҗҺ пјҢ е·®жҜ”е’Ңз®—жі•еңЁеҶ…зҺҜзҡ„иҫ“еҮәиҜҜе·®еӣҫеғҸж–ңзҺҮйӘӨйҷҚ пјҢ зі»з»ҹзјәд№ҸйІҒжЈ’жҖ§ гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
в–І еӣҫC2.2.3 ејҜйҒ“еҶ…з®—жі•жҜ”иҫғ
з”ұеӣҫC2.2.3еҸҜд»ҘзңӢеҮә пјҢ е°ҸиҪҰеҹәжң¬иҝӣе…ҘејҜйҒ“еҶ… пјҢ жӯӨж—¶е·®жҜ”е’ҢеңЁеӨ–зҺҜзҡ„иҫ“еҮәжӣІзәҝе·Із»ҸеҮәзҺ°иҙҹж–ңзҺҮ пјҢ йҡҫд»Ҙз»ҙжҢҒиҙҹеҸҚйҰҲ пјҢ жӯӨж—¶е°ҸиҪҰиӢҘжҳҜеҸ—еҲ°дёҖе®ҡзЁӢеәҰзҡ„жү°еҠЁ пјҢ еҫҲеҸҜиғҪеӣ и¶…еҮәз®—жі•жүҝеҸ—йҳҲеҖјдә§з”ҹиҝҮи°ғжҠ–еҠЁз”ҡиҮіеҶІеҮәиөӣйҒ“ гҖӮ зӣёеҸҚзҡ„ пјҢ е·®жҜ”е’Ңе·®з®—жі•зҡ„иҫ“еҮәиҜҜе·®жӣІзәҝе’Ңе…¶д»–е…ҘејҜйҳ¶ж®өзҡ„и¶ӢеҠҝеҹәжң¬дҝқжҢҒдёҖиҮҙ гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
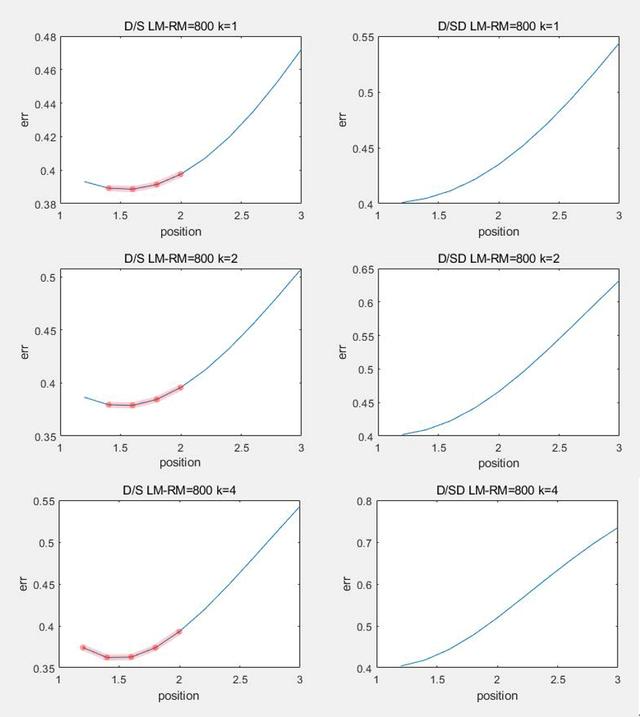
в–І еӣҫC2.2.4 зҗҶжғіеҒҮи®ҫ
иӢҘжҳҜLM-RM继з»ӯеўһеӨ§еҲ°дёҖдёӘе®һйҷ…йҡҫд»ҘиҫҫеҲ°зҡ„ж•°еҖј пјҢ еҸҜд»ҘзңӢеҲ°е·®жҜ”е’Ңз®—жі•е·Із»Ҹеҙ©жәғ пјҢ дҪҶжҳҜе·®жҜ”е’Ңе·®з®—жі•д»Қ然дҝқжҢҒе…¶еҺҹжңүзү№жҖ§дёҚеҸҳ гҖӮ
з”ұжӯӨеҸҜд»ҘиҜҒжҳҺ пјҢ з”өж„ҹе·®жҜ”е’Ңе·®еҠ жқғз®—жі• пјҢ зӣёиҫғз”өж„ҹе·®жҜ”е’ҢеҠ жқғз®—жі•еҜ№ејҜйҒ“жңүзқҖжӣҙй«ҳзҡ„жӢҹеҗҲеәҰ пјҢ жӣҙеҠ иғҪеӨҹйҖӮеә”еӨ–з•Ңе№Іжү° гҖӮ
2.3 иҝӣиЎҢдёҚеҗҢз®—жі•еҠЁжҖҒе…ҘејҜзҒөж•ҸеәҰжҜ”иҫғе°Ҷе…¬ејҸC5еҸҳејҸ пјҢ еҫ—:
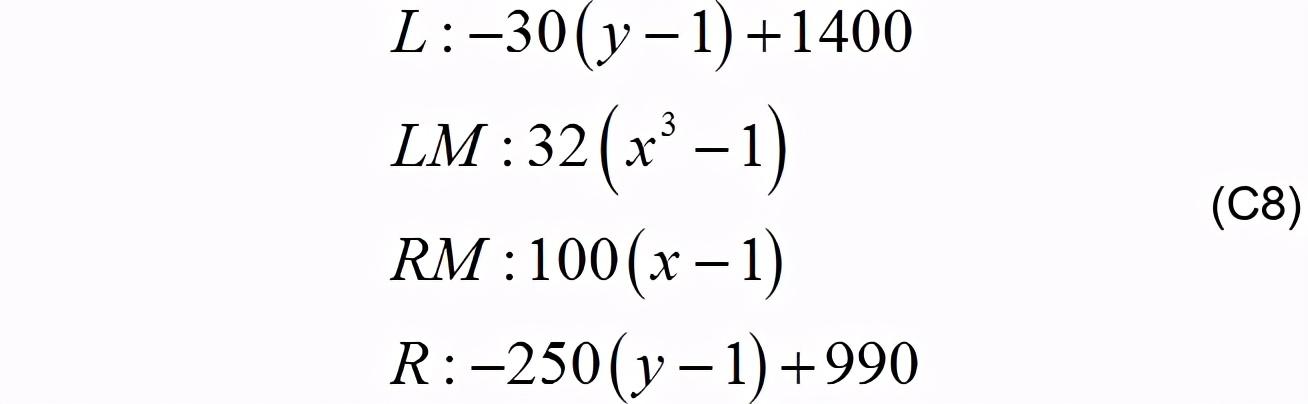 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
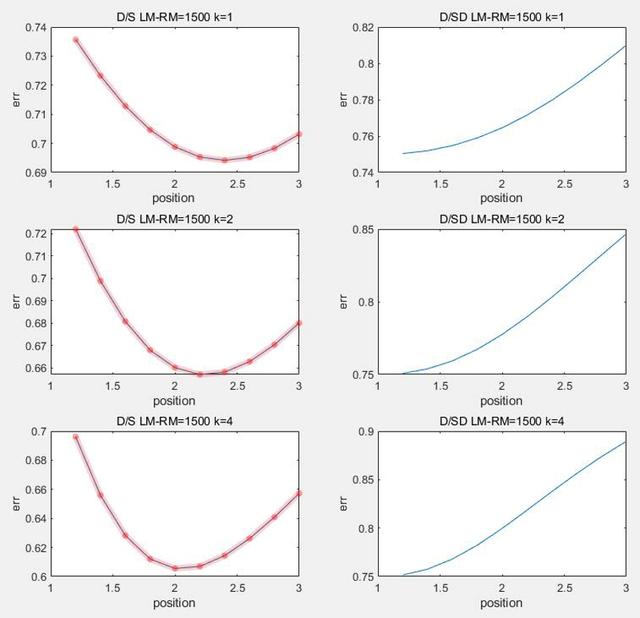
д»Је…Ҙе…Ҙе…¬ејҸC6,C7 пјҢ дҪҝз”ЁMATLABеҜ№x,y,errиҝӣиЎҢдёүз»ҙе»әжЁЎ пјҢ з»“жһңеҰӮеӣҫC2.3.1 гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
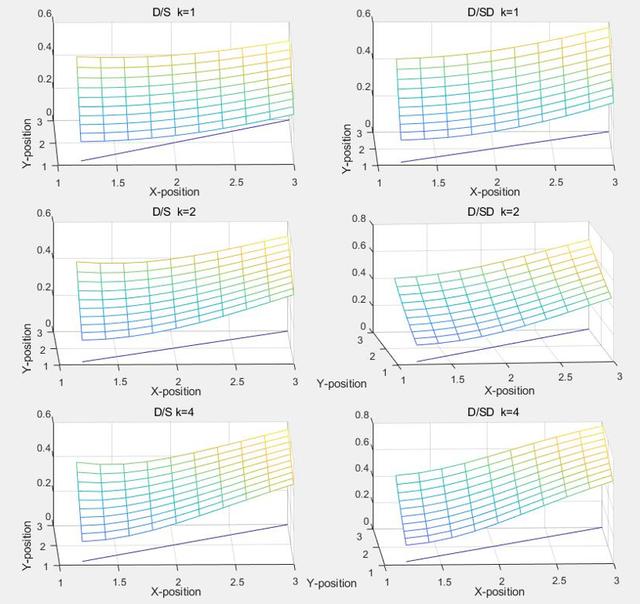
в–І еӣҫC2.3.1 дёүз»ҙжЁЎеһӢ
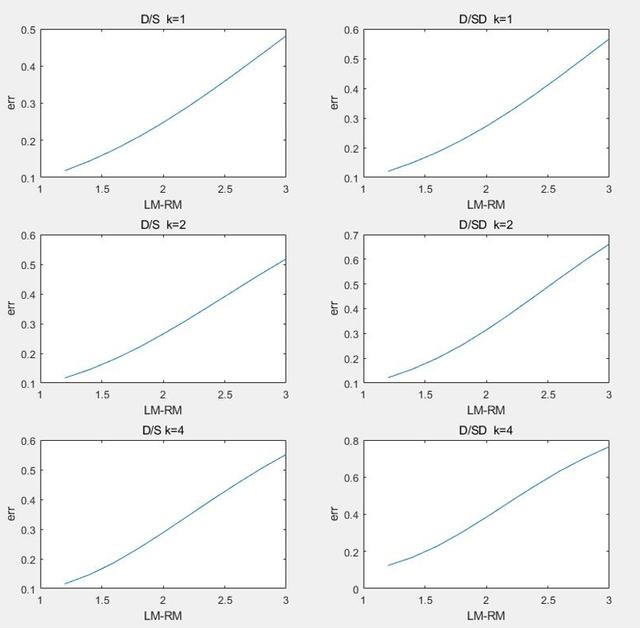
еңЁдёүз»ҙеӣҫеғҸдёӯ пјҢ йҷӨе·®жҜ”е’Ңе·®еҠ жқғз®—жі•жІЎжңүе·®жҜ”е’ҢеҠ жқғз®—жі•жүҖдә§з”ҹзҡ„иҫ№зјҳдёҠеҚ·зҺ°иұЎпјҲеҜ№еә”еӣҫC2.2.3,C2.2.4дёӯж–ңзҺҮзҝ»иҪ¬еҢәеҹҹпјү пјҢ жІЎжңүеҸ‘зҺ°жҳҺжҳҫзү№еҫҒ пјҢ ж•…е°қиҜ•жІҝY=XеҜ№дёүз»ҙеӣҫеғҸжҠҪж · пјҢ иҝӣдёҖжӯҘиҝӣиЎҢеҲҶжһҗ пјҢ жҠҪж ·еҗҺеҰӮеӣҫC2.3.2 гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
в–І еӣҫC2.3.2 жҠҪж ·еҗҺжӣІзәҝ
жҠҪж ·еҗҺеҚідёәе°ҸиҪҰжҢҒз»ӯжІҝдёӯзәҝиө°ж—¶зҡ„иҜҜе·®еҸҚйҰҲ пјҢ еҸ‘зҺ°е·®жҜ”е’ҢеҠ жқғз®—жі•дёҺе·®жҜ”е’Ңе·®еҠ жқғз®—жі•зҡ„зҒөж•ҸеәҰе·®ејӮ并дёҚжҳҺжҳҫ гҖӮ з»“еҗҲC2.1зҡ„йқҷжҖҒеҲҶжһҗ пјҢ жҺЁж–ӯе·®жҜ”е’Ңз®—жі•еҜ№ејҜйҒ“жңүжӣҙй«ҳзҒөж•ҸеәҰзҡ„еҺҹеӣ жҳҜе°ҸиҪҰе…ҘејҜж—¶еҫҖеҫҖжңүеҲҮеӨ–зҺҜзҡ„и¶ӢеҠҝ пјҢ е·®жҜ”е’Ңе·®з®—жі•иғҪеӨҹжҸҗдҫӣжӣҙеҠ зЁіе®ҡзҡ„иҙҹеҸҚйҰҲжүҖиҮҙ гҖӮ
C2.4 е·®жҜ”е’Ңе·®еҠ жқғз®—жі•еҜ№жҜ”е·®жҜ”е’Ңдёӯй—ҙз”өж„ҹеҒҸзҪ®з®—жі•зҡ„дјҳеҠҝжңӘеҠ жҜ”дҫӢзі»ж•°ж—¶ пјҢ е·®жҜ”е’Ңз®—жі•дјҡе°Ҷиҫ“еҮәиҜҜе·®йҷҗеҲ¶еңЁ1д»ҘеҶ… пјҢ дҪҶжҳҜе·®жҜ”е’Ңе·®еҠ жқғз®—жі•жҳҫ然зӘҒз ҙдәҶиҝҷдёҖйҷҗеҲ¶ пјҢ иҝҷд№ҹд»ЈиЎЁзқҖе·®жҜ”е’Ңе·®еҠ жқғз®—жі•жҚҹеӨұдәҶдёҖе®ҡзҡ„иөӣйҒ“йҖӮеә”жҖ§ пјҢ жҜҸж¬Ўжӣҙж–°иөӣйҒ“ пјҢ еңЁеҸӮж•°дёҠйғҪиҰҒиҝӣиЎҢдёҖе®ҡзЁӢеәҰзҡ„дҝ®ж”№ гҖӮ д№ҹе°ұжҳҜиҜҙ пјҢ е·®жҜ”е’Ңе·®еҠ жқғз®—жі•дёҚиғҪеғҸе·®жҜ”е’ҢдёҖж · пјҢ еӣ дёәе…¶еҜ№дәҺеҗ„з§ҚиөӣйҒ“йҖӮеә”жҖ§й«ҳзҡ„дјҳеҠҝ规йҒҝдёҺе…¶д»–ж— жӯӨзұ»дјҳеҠҝз®—жі•зҡ„з«һдәү гҖӮ
иҝҷе°ұдёҚеҫ—дёҚеҶҚи°ҲдёҖдёӢе…¬ејҸC6:
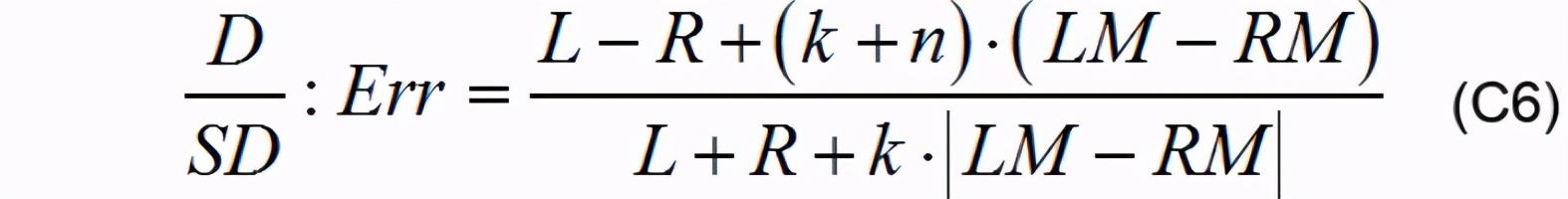 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
еҸҜд»ҘзңӢеҲ° пјҢ еҲҶеӯҗе’ҢеҲҶжҜҚдёҠйғҪжңү(LM-RM)еҸӮдёҺиҝҗз®— пјҢ дёҚйҡҫзңӢеҮә(L-R)жҳҜдёҖе®ҡе°ҸдәҺ(L+R)зҡ„ пјҢ йӮЈд№ҲзҗҶи®әдёҠеҸӘиҰҒдёҚеҮәзҺ°kжҜ”k+nеӨ§еҲ°дёҖе®ҡзЁӢеәҰзҡ„жғ…еҶөдёӢ пјҢ иҜҘе…¬ејҸеҸҜд»ҘзңӢдҪңдј з»ҹзҡ„е·ҰеҸіж°ҙе№із”өж„ҹе·®жҜ”е’ҢеҠ жқғ пјҢ еҶҚеҠ дёҠдёҖйғЁеҲҶ(LM-RM)зҡ„еҠ жқғ пјҢ йӮЈд№Ҳй—®йўҳе°ұдә§з”ҹдәҶ пјҢ дёәд»Җд№ҲжҲ‘йҖүжӢ©з”өж„ҹе·®жҜ”е’Ңе·®еҠ жқғз®—жі• пјҢ иҖҢдёҚжҳҜзӣҙжҺҘеңЁж°ҙе№із”өж„ҹе·®жҜ”е’Ңз®—жі•еҗҺ пјҢ еҠ дёҠдёҖдёӘеёҰжҜ”дҫӢзі»ж•°зҡ„(LM-RM)жқҘеҒҸзҪ®е‘ўпјҹ
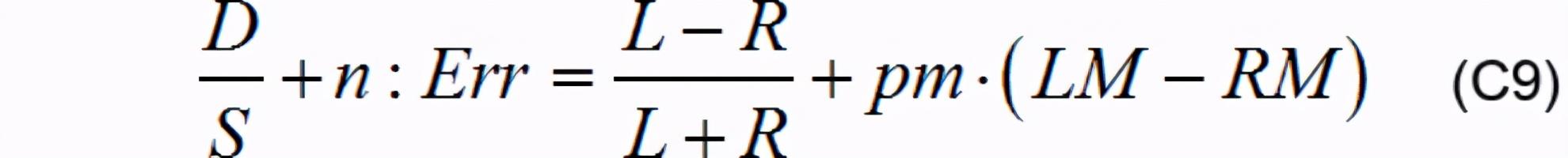 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
йҰ–е…Ҳ пјҢ йҖҡиҝҮи§ӮеҜҹеҸҜд»Ҙеҫ—еҮә第дёҖдёӘз»“и®ә пјҢ е…¬ејҸC9зҡ„и°ғиҜ•иҝҮдәҺеӨҚжқӮ пјҢ е·®жҜ”е’ҢеҠ жқғз®—жі•еңЁжІЎжңүжҜ”дҫӢзі»ж•°зҡ„жғ…еҶөдёӢ пјҢ иҫ“еҮәжҳҜдёҖдёӘе°ҸдәҺ1зҡ„ж•° пјҢ иҖҢ(LM-RM)зҡ„еҖјеӨӘеӨ§дәҶ пјҢ йңҖиҰҒе°Ҷе…¶д№ҳдёҠдёҖдёӘйқһеёёе°Ҹзҡ„ж•° пјҢ жҲ–иҖ…е°Ҷе·®жҜ”е’Ңиҝҗз®—еҗҺд№ҳдёҠдёҖдёӘйқһеёёеӨ§зҡ„ж•° пјҢ жүҚиғҪдҪҝеҒҸзҪ®йЎ№е’Ңе·®жҜ”е’Ңдә’зӣёеҢ№й…Қ гҖӮ 并且 пјҢ иҝҷд№ҲеҒҡеҸҲдјҡдә§з”ҹдёҖдёӘжӣҙеӨ§зҡ„й—®йўҳ пјҢ еҚіе“ӘжҖ•дҝЎеҸ·жәҗжҲ–иөӣйҒ“дә§з”ҹдәҶдёҖдёқзҡ„еҸҳеҢ– пјҢ е…¶еҪұе“ҚйғҪдјҡеңЁејҸеӯҗдёӯиў«ж”ҫеӨ§ пјҢ з®—жі•зҡ„зЁіе®ҡжҖ§е“ӘжҖ•жҜ”дёҠе°Ҷ(LM-RM)гҖҒ(L-R)зӣҙжҺҘд№ҳд»ҘжҜ”дҫӢзі»ж•°дҪңдёәиҜҜе·®иҫ“еҮәзҡ„з®—жі•иҝҳиҰҒе·®еҫ—еӨҡ гҖӮ
жҺЁиҚҗйҳ…иҜ»
- е°Ҹзұі11иғҪжЈҖжөӢеҝғзҺҮпјҡеҮҶзЎ®еәҰе ӘжҜ”жҷәиғҪжүӢиЎЁ
- иҒ”жғіеҸ‘еёғжҷәиғҪзңјй•ң ThinkReality A3
- зғҹеҸ°жёҜвҖңз®ЎйҒ“жҷәи„‘зі»з»ҹвҖқдёҠзәҝ еңЁеӣҪеҶ…зҺҮе…Ҳе®һзҺ°еҺҹжІ№еӮЁиҝҗе…ЁжҒҜжҷәиғҪжҺ’дә§
- е”җеұұеӣӣз»ҙжҷәиғҪ科жҠҖжңүйҷҗе…¬еҸёпјҡеҸҢиҮӮжңәеҷЁдәәеј•йўҶдәәжңәеҚҸдҪңж–°зәӘе…ғ
- з”өи„‘жҠҘ2020е№ҙеәҰиҺ·еҘ–дә§е“Ғпјҡеј•йўҶжҷәиғҪе•ҶеҠЎж— зәҝжҠ•еҪұж—¶д»Јзҡ„жҳҺеҹәEзі»еҲ—е•ҶеҠЎжҠ•еҪұжңә
- е…іжіЁ | 马ж–Ҝе…ӢзӘҒ然宣еёғпјҡзү№ж–ҜжӢүжҲ–е°ҶиҝҺжқҘйҰ–еұҠвҖңдәәе·ҘжҷәиғҪж—ҘвҖқ
- иҒ”жғіжӯЈејҖеҸ‘дёӢдёҖд»ЈThinkRealityжҷәиғҪзңјй•ң
- 199е…ғ е°Ҹзұіжңүе“Ғдј—зӯ№жҷәиғҪеҒҘи…№иҪ®пјҡLEDж•°жҳҫ иҪ»жқҫз»ғеҮә马甲зәҝ
- жҷәиғҪжүӢжңәж—¶д»ЈпјҢз”өжұ и¶ҠжқҘи¶ҠдёҚз»Ҹз”ЁпјҢжҖҺд№Ҳе……з”өжүҚиғҪ延й•ҝз”өи§ҶеҜҝе‘Ҫпјҹ
- дәәе·ҘжҷәиғҪ|йә»иҫЈиҙўз»ҸпјҡжҲ‘еӣҪвҖңз®—еҠӣвҖқеўһй•ҝиҝ…йҖҹпјҢжңүеҠӣж”Ҝж’‘дәәе·ҘжҷәиғҪеҸ‘еұ•


















