жҷәиғҪиҪҰз”өж„ҹе·®жҜ”е’Ңе·®еҠ жқғз®—жі•з ”з©¶( дәҢ )
жӯӨеӨ– пјҢ з”ұдәҺеңЁй•ҝзӣҙйҒ“дёҠ пјҢ LMе’ҢRMзҡ„еҖји¶Ӣиҝ‘дәҺ0 пјҢ жүҖд»Ҙжӣҙж”№еҗҺзҡ„ејҸеӯҗеҜ№е°ҸиҪҰеңЁй•ҝзӣҙйҒ“дёҠиЎҢ驶时еҮ д№ҺжІЎжңүеҪұе“Қ гҖӮ
1.2 з®—жі•зҡ„жһ„йҖ дёәиҝӣдёҖжӯҘиҜҒе®һзҗҶи®әеҒҮи®ҫзҡ„еҗҲзҗҶжҖ§ пјҢ еҜ№з®—жі•иҝӣдёҖжӯҘзҡ„дҝ®ж”№ пјҢ жӣҙж”№еҗҺе…¬ејҸдёәпјҡ
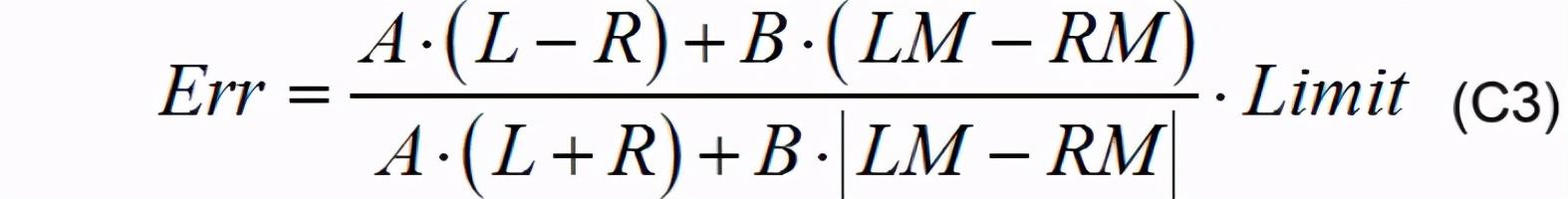 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
дҪҝз”Ёе…¬ејҸC3 пјҢ е°ҸиҪҰйЎәж—¶й’ҲгҖҒйҖҶж—¶й’ҲеҲҶеҲ«еҸ‘иҪҰ пјҢ и§ӮеҜҹе…¶е·®еҲ«д»ҘеҸҠеҜ№ејҜйҒ“зҡ„жӢҹеҗҲзЁӢеәҰ гҖӮ жөӢиҜ•з»“жһңиЎЁжҳҺ пјҢ дҪҝз”Ёе…¬ејҸC3иҝӣиЎҢжөӢиҜ•зҡ„е°ҸиҪҰ пјҢ еңЁйЎәгҖҒйҖҶж—¶й’ҲиЎҢ驶时ж•ҲжһңеҮ д№ҺзӣёеҗҢ пјҢ 并且еҜ№дәҺејҜйҒ“зҡ„жӢҹеҗҲзЁӢеәҰе’Ңж•Ҹж„ҹжҖ§зҡҶй«ҳдәҺдҪҝз”Ёе…¬ејҸC1ж—¶зҡ„жөӢиҜ•з»“жһң гҖӮ
з”ұдәҺз®—жі•зҡ„ж”№еҸҳ пјҢ еҲҶеӯҗдёҺеҲҶжҜҚдёҠ(LM+RM)еҠ жқғзі»ж•°жҳҫ然дёҚеҶҚйңҖиҰҒдҝқжҢҒдёҖиҮҙ гҖӮ еҜ№з®—жі•еҸӮж•°иҝӣиЎҢи°ғж•ҙеҗҺеҫ—еҲ°дәҶдёҖеҘ—зЁіе®ҡзҡ„зӣҙйҒ“ејҜйҒ“иЎҢ驶方жЎҲ пјҢ дҪҝз”Ёе…¬ејҸC4 гҖӮ
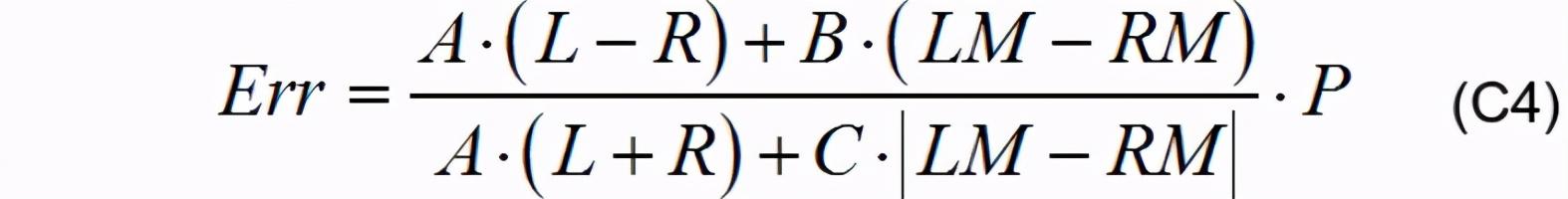 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
е…¬ејҸC4еҚідёәе·®жҜ”е’Ңе·®еҠ жқғз®—жі•зҡ„жңҖз»ҲејҸ пјҢ з”ұдәҺеҺҹLIMITзі»ж•°дёҚеҶҚиө·йҷҗе№…дҪңз”Ё пјҢ ж”№дҪңжҜ”дҫӢзі»ж•°P гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
2.1 жһ„йҖ е°ҸиҪҰиҝҮејҜз”өж„ҹеҖјеҸҳеҢ–жЁЎеһӢж¬ІеҜ№з®—жі•иҝӣиЎҢе»әжЁЎиҜҒжҳҺ пјҢ йҰ–е…ҲиҰҒеҜ№е°ҸиҪҰиҝҮејҜж—¶ пјҢ е·ҰгҖҒеҸіз”өж„ҹзҡ„еҸҳеҢ–еҮҪж•°иҝӣиЎҢе»әжЁЎ гҖӮ зҺ°е°Ҷе°ҸиҪҰзҪ®дәҺзӣҙйҒ“дёҺејҜйҒ“зӣёжҺҘеӨ„ пјҢ дҪҝе…¶з”өж„ҹеүҚзһ»дҪҚдәҺзӣҙйҒ“дёҺејҜйҒ“дәӨзәҝжӯЈдёҠж–№ пјҢ 并е°Ҷе°ҸиҪҰжІҝдёӯзәҝзј“зј“еҗ‘еүҚжҺЁ пјҢ жҜҸйҡ”зӣёеҗҢи·қзҰ»и®°еҪ•з”өж„ҹж•°жҚ® пјҢ зӣҙеҲ°е·ҰгҖҒеҸіз”өж„ҹж•°жҚ®ж— жҳҺжҳҫеҸҳеҢ–ж—¶дёәжӯў гҖӮ
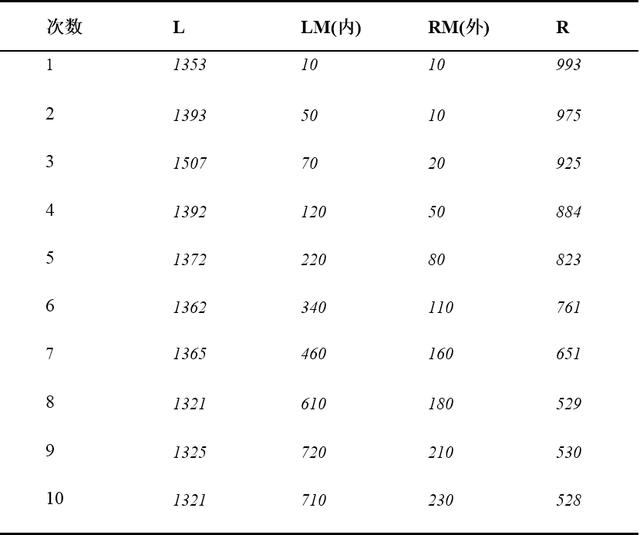
жөӢеҫ—е°ҸиҪҰеӣӣдёӘз”өж„ҹеҖјеҰӮдёӢиЎЁпјҡ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
в–І иЎЁC2.1 з”өж„ҹйҮҮж ·иЎЁ
гҖҗжҷәиғҪиҪҰз”өж„ҹе·®жҜ”е’Ңе·®еҠ жқғз®—жі•з ”з©¶гҖ‘еҲҶжһҗгҖҒжқғиЎЎ пјҢ дҪҝз”Ёд»ҘдёӢеҮҪж•°еҜ№еӣӣдёӘз”өж„ҹж•°еҖјеҸҳеҢ–иҝӣиЎҢжӢҹеҗҲпјҡ
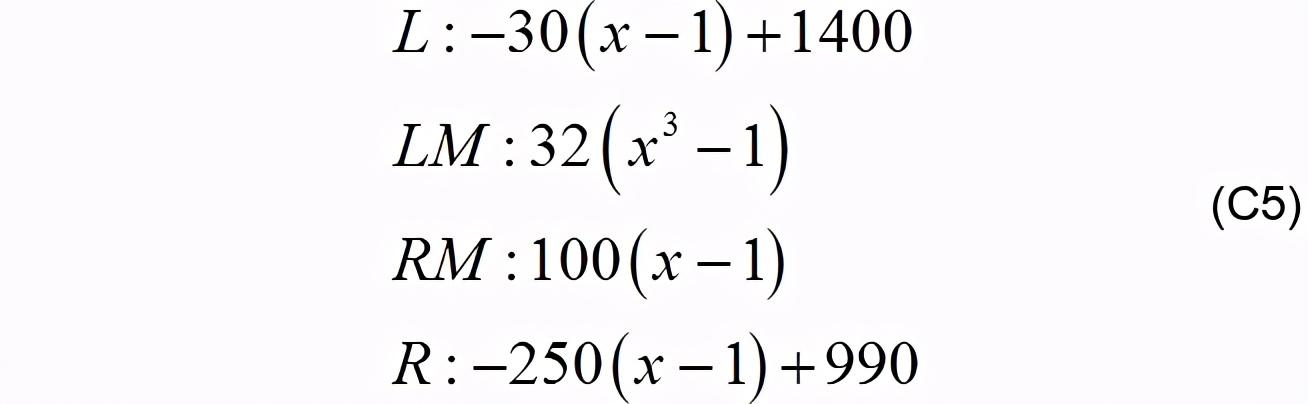 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
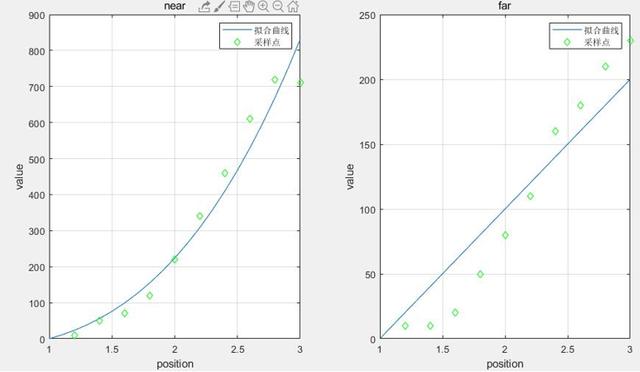
жӢҹеҗҲж•ҲжһңеҰӮеӣҫC2.1.1,C2.1.2 гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
в–І еӣҫC2.1.1 з”өж„ҹLMпјҲе·Ұпјү,RMпјҲеҸіпјүжӢҹеҗҲж•Ҳжһң
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
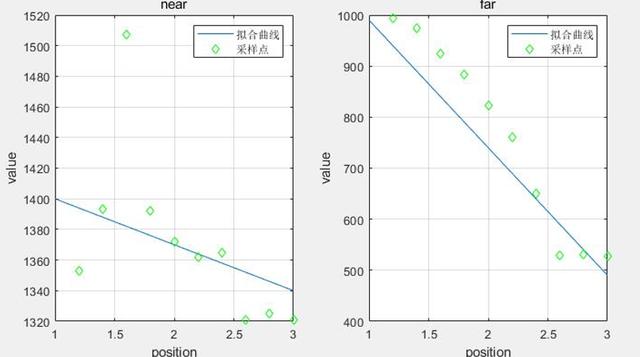
в–І еӣҫC2.1.2 з”өж„ҹLпјҲе·Ұпјү,RпјҲеҸіпјүжӢҹеҗҲж•Ҳжһң
2.2 иҝӣиЎҢдёҚеҗҢз®—жі•дҪҚдәҺзӣёеҗҢдҪҚзҪ®зҡ„еҶ…гҖҒеӨ–зҺҜеҸҚйҰҲжҜ”иҫғз”ұдәҺйҮҮйӣҶз”өж„ҹеҖјж—¶ пјҢ ж—¶еҲ»дҝқжҢҒе°ҸиҪҰдҪҚдәҺиөӣйҒ“жӯЈдёӯ пјҢ ж•…иҝҳйңҖиҰҒз ”з©¶е°ҸиҪҰдҪҚдәҺеҶ…зҺҜдёҺеӨ–зҺҜзҡ„е·®ејӮ гҖӮ з”ұдәҺе°ҸиҪҰе·ҰгҖҒеҸіж°ҙе№із”өж„ҹпјҲL,RпјүеҸ—еҲ°е°ҸиҪҰе·ҰгҖҒеҸідҪҚзҪ®еҪұе“ҚдёҚеӨ§ пјҢ иҖҢеҸ—е°ҸиҪҰеүҚгҖҒеҗҺдҪҚзҪ®еҪұе“ҚиҫғеӨ§ пјҢ йҮҮеҸ–еӣәе®ҡLгҖҒRеҖјзҡ„ж–№ејҸжқҘзЎ®и®Өе°ҸиҪҰзҡ„дҪҚзҪ® пјҢ е№¶з ”з©¶иҫ“еҮәиҜҜе·®errйҡҸLMгҖҒRMеҸҳеҢ–规еҫӢ гҖӮ
з”ұйҮҮйӣҶеҫ—еҲ°з”өж„ҹеҖјеҸҜд»Ҙеҫ—еҲ°е°ҸиҪҰе…ҘејҜзЁӢеәҰзӣёеҗҢж—¶ пјҢ дёҚеҗҢдҪҚзҪ®(L+R)гҖҒ(L-R)зҡ„еҖјеҸҳеҢ–дёҚеӨ§ пјҢ иҖҢLMгҖҒRMеҸҳеҢ–иҫғеӨ§ пјҢ жүҖд»Ҙеӣәе®ҡLгҖҒRзҡ„еҖјжқҘиЎЁеҫҒе°ҸиҪҰе…ҘејҜзҡ„зЁӢеәҰ пјҢ ж №жҚ®е…¬ејҸе»әз«Ӣд»ҘдёӢеҮҪж•°жЁЎеһӢпјҡ
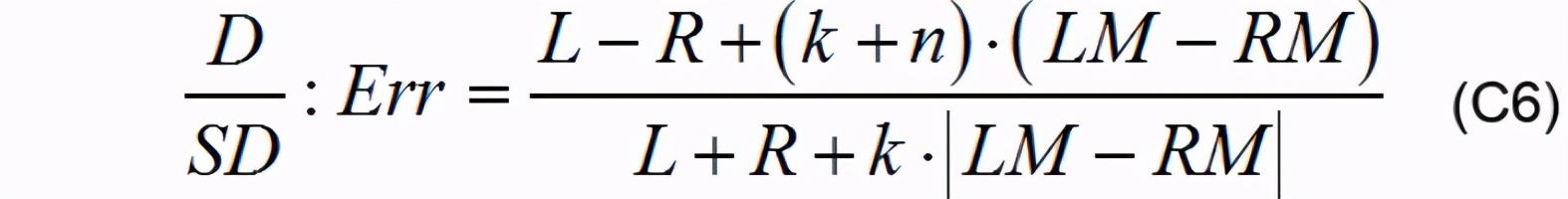 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
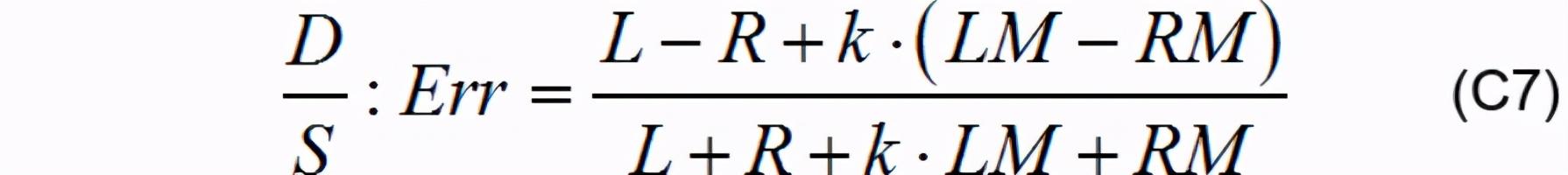 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
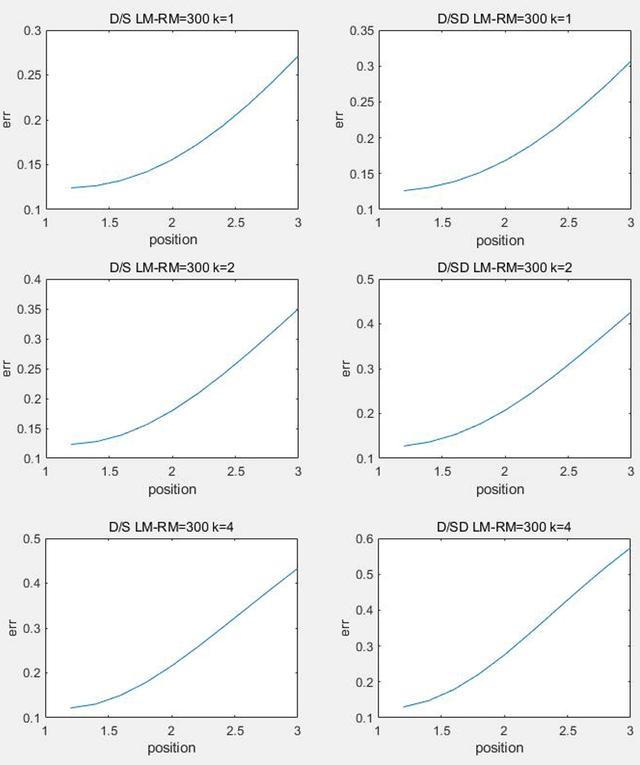
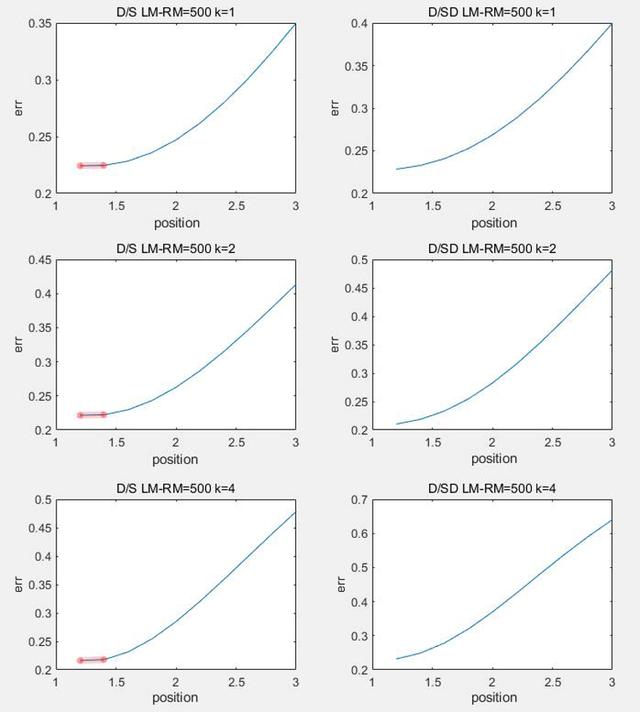
еҲҶеҲ«еҸ–n=0жғ…еҶөдёӢL-R=300,L+R=2400;L-R=500,L+R=2200;L-R=800,L+R=2000жқҘиЎЁзӨәе°ҸиҪҰеҲҡеҲҡејҖе§Ӣе…ҘејҜ пјҢ е°ҸиҪҰеҹәжң¬иҝӣе…ҘејҜйҒ“ пјҢ е°ҸиҪҰе®Ңе…Ёиҝӣе…ҘејҜйҒ“ пјҢ 并дҪҝз”Ёе…¬ејҸC5жқҘи®Ўз®—(LM-RM),(LM+RM) пјҢ дҪҝз”ЁMATLABз”»еҮәиҫ“еҮәиҜҜе·®дёҺе°ҸиҪҰдҪҚзҪ®е…ізі» гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
в–І еӣҫC2.2.1 е…ҘејҜеҲқжңҹз®—жі•жҜ”иҫғ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
жҺЁиҚҗйҳ…иҜ»
- е°Ҹзұі11иғҪжЈҖжөӢеҝғзҺҮпјҡеҮҶзЎ®еәҰе ӘжҜ”жҷәиғҪжүӢиЎЁ
- иҒ”жғіеҸ‘еёғжҷәиғҪзңјй•ң ThinkReality A3
- зғҹеҸ°жёҜвҖңз®ЎйҒ“жҷәи„‘зі»з»ҹвҖқдёҠзәҝ еңЁеӣҪеҶ…зҺҮе…Ҳе®һзҺ°еҺҹжІ№еӮЁиҝҗе…ЁжҒҜжҷәиғҪжҺ’дә§
- е”җеұұеӣӣз»ҙжҷәиғҪ科жҠҖжңүйҷҗе…¬еҸёпјҡеҸҢиҮӮжңәеҷЁдәәеј•йўҶдәәжңәеҚҸдҪңж–°зәӘе…ғ
- з”өи„‘жҠҘ2020е№ҙеәҰиҺ·еҘ–дә§е“Ғпјҡеј•йўҶжҷәиғҪе•ҶеҠЎж— зәҝжҠ•еҪұж—¶д»Јзҡ„жҳҺеҹәEзі»еҲ—е•ҶеҠЎжҠ•еҪұжңә
- е…іжіЁ | 马ж–Ҝе…ӢзӘҒ然宣еёғпјҡзү№ж–ҜжӢүжҲ–е°ҶиҝҺжқҘйҰ–еұҠвҖңдәәе·ҘжҷәиғҪж—ҘвҖқ
- иҒ”жғіжӯЈејҖеҸ‘дёӢдёҖд»ЈThinkRealityжҷәиғҪзңјй•ң
- 199е…ғ е°Ҹзұіжңүе“Ғдј—зӯ№жҷәиғҪеҒҘи…№иҪ®пјҡLEDж•°жҳҫ иҪ»жқҫз»ғеҮә马甲зәҝ
- жҷәиғҪжүӢжңәж—¶д»ЈпјҢз”өжұ и¶ҠжқҘи¶ҠдёҚз»Ҹз”ЁпјҢжҖҺд№Ҳе……з”өжүҚиғҪ延й•ҝз”өи§ҶеҜҝе‘Ҫпјҹ
- дәәе·ҘжҷәиғҪ|йә»иҫЈиҙўз»ҸпјҡжҲ‘еӣҪвҖңз®—еҠӣвҖқеўһй•ҝиҝ…йҖҹпјҢжңүеҠӣж”Ҝж’‘дәәе·ҘжҷәиғҪеҸ‘еұ•


















