江苏龙网

  1. 首页 > 人文 > >

作为码农，你无需成为数学家即可掌握量子计算( 二 )


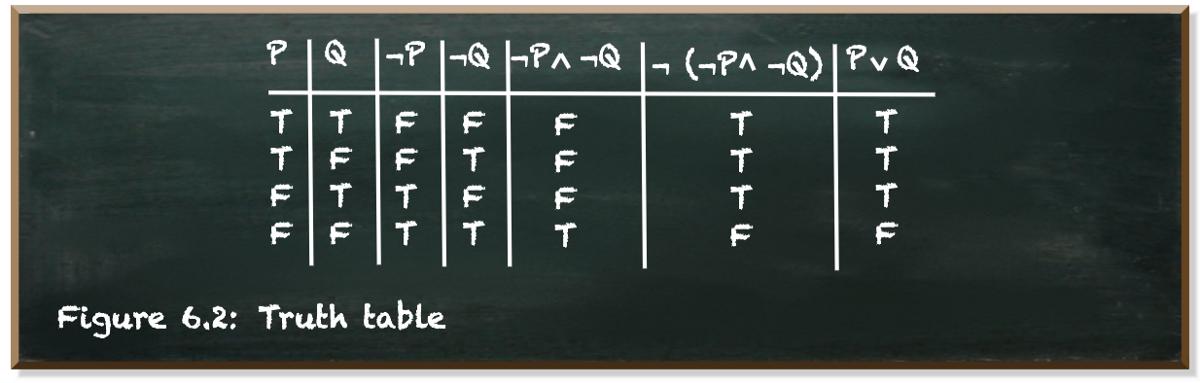
我们有两个变量P和Q 。 每个变量都是true（T）或false（F） 。根据它们的值的组合 ， 我们可以推导出任何布尔语句的值 。下图描述了P ， Q ， 不是P ， 不是Q ， 不是P和不是Q ， 不是（不是P和不是Q）以及P或Q的真值表 。
作为码农，你无需成为数学家即可掌握量子计算文章插图
> Image by author, Frank Zickert
该真值表显示P或Q等于not（不是P而不是Q） 。这种逻辑上的对等告诉我们 ， 我们甚至不需要运算符or 。我们可以用not（不是P而不是Q）代替它 。
但是P或Q简洁明了 ， 更容易理解 。
"如果我们的编程语言中没有操作符 ， 该怎么办？"
精明的程序员将编写自己的运算符 。
P | Q | P or Q--------------T | T | TrueT | F | TrueF | T | TrueF | F | False
这就是编程的全部意义 。程序员编写会产生某种行为的函数 。他们使用并结合了这些功能 ， 以创建更多甚至表现出复杂行为的功能 。他们编写的整个程序归结为一系列巧妙组合的功能 。程序员使用他们的编译器（或解释器）将高层功能转换为非常基本的布尔逻辑 。而且这种基本的布尔逻辑可以使用电气开关来执行 。开关及其组合称为门 。当我们连接门时 ， 它们形成一个电路 。
计算机以不连续的时间间隔通过电路发送电脉冲 。如果在适当的时间收到电脉冲 ， 则将其解释为1（真） 。如果未收到脉冲 ， 则将其解释为0（false） 。
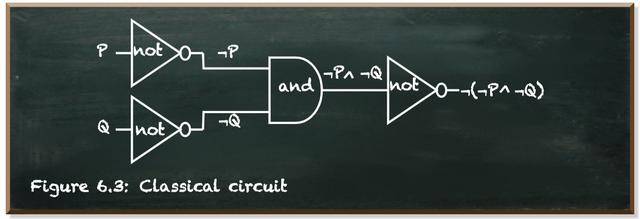
尽管有名称 ， 但关于电路没有任何通告 。它们是线性的 ， 从左到右读取 。让我们看一个与我们之前看过的布尔函数相对应的例子
下图描绘了非（非P和非Q）的电路图 。该电路从左侧接收输入 ， 然后向右侧输出 。
作为码农，你无需成为数学家即可掌握量子计算文章插图
> Image by author, Frank Zickert
这样的门和电路是任何现代计算机的基础 。这包括量子计算机 。尽管量子力学的世界不同 ， 但量子计算的世界却惊人地相似 。
不要让自己对所有的数学公式感到眼花 。 乱 。它们是概念的表示 。不多不少 。
让我们回到介绍公式：
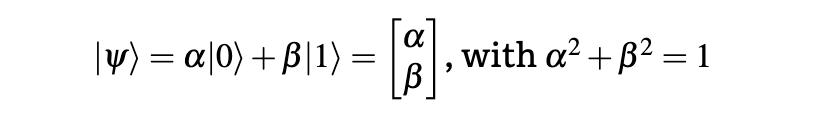作为码农，你无需成为数学家即可掌握量子计算文章插图
它是量子态|ψ?（" psi"）的数学符号 。当经典位的状态为布尔值（0表示错误或1表示真）时 ， 量子位（qubit）的状态是量子状态|0?和|1?的重合 ， 由α和β加权 。
在这种叠加状态下 ， 除非进行测量 ， 否则量子系统既不是0也不是1 。仅当测量量子位时 ， 状态才会崩溃为0或1 。 两个权重（α^ 2）和（β^ 2）的平方表示测量0或1的概率 。 α越大 ， 则权重越大 测量0的概率 。 分别地 ， β越大 ， 测量1的概率就越高 。
公式说明了更多内容 。它说量子态是两个权重[αβ]的向量 。
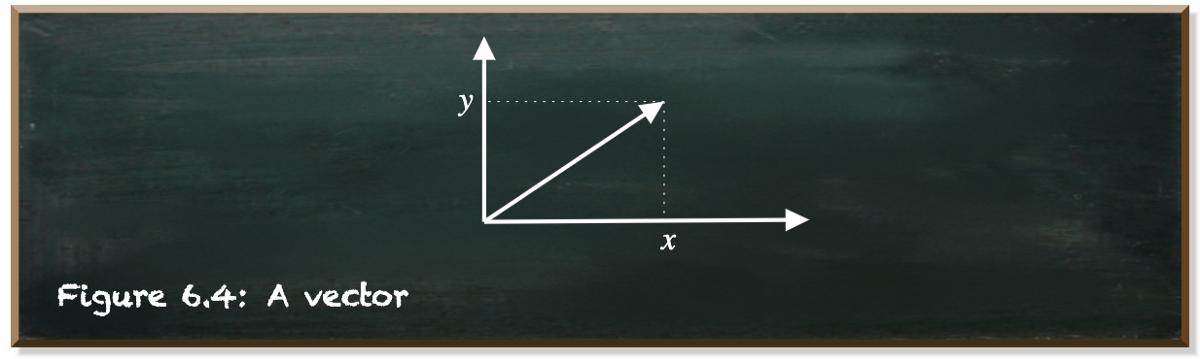
向量是具有大小和方向的地理对象 。如果在坐标系中绘制 ， 则矢量从中心开始 ， 在矢量中的数字指定的点结束 。
作为码农，你无需成为数学家即可掌握量子计算文章插图
> Image by author, Frank Zickert
在Python中 ， 向量是一个数组 。因此 ， 量子位的状态是阵列α ， β 。并且 ， alpha和beta是数字变量 。量子态是两个数字的数组 。
但是 ， 两个数字组成的数组比布尔值复杂得多 。布尔值为True或False 。您可以使用简单的运算符（例如not和and和and or）转换布尔值 。您可以推断真值表中布尔值的转换 。
但是 ， 如何转换两个数字组成的数组？ 您如何推理这种转变？
显而易见的答案是数学 。但这不是唯一可能的答案 。让我们使用Python 。
----------- Reversed states: ----------psi: [0.50, 0.87] result: [0.87, 0.50]|0>: [1.00, 0.00] result: [0.00, 1.00]|1>: [0.00, 1.00] result: [1.00, 0.00]


推荐阅读


上一篇：教你给手机设置“特效壁纸”，实现桌面分屏

下一篇：PS5官方拆机演示：内部硬件一览无余