江苏龙网

  1. 首页 > 人文 > >

作为码农，你无需成为数学家即可掌握量子计算( 四 )


到目前为止 ， 我们使用了Python的内置函数反转 。尽管这很方便 ， 但我们实际上看不到它在内部如何工作 。让我们使用另一个函数 。自制功能 。
reversed psi: [0.87, 0.50]
我们定义一个函数Adjust_weight（第1行） 。它具有量子态和权重 。两者都是具有两个项目的数组 。它将位置0的值相乘 ， 然后将位置1的值相乘 。 它返回这两个乘积的总和（第2行） 。
我们可以使用此功能来反转psi 。对于adjust_weight返回一个数字 ， 我们将其调用两次以返回两个项目的数组（第5行和第6行） 。在此示例中 ， 我们没有显式创建数组 ， 而是将这些值直接打印到控制台（第4行） 。
在这两个调用中 ， 我们都提供原始的psi作为状态参数 。在第一个调用中 ， 其结果是反转psi的第一个数字 ， 我们提供[0,1]作为权重 。这意味着 ， 我们得到的0乘以第一个psi数 ， 再乘以1乘以第二个psi数 。该总和是原始psi的第二个数字 。
在第二个调用中 ， 其结果是psi的第二个倒数 ， 我们提供[1,0]作为权重 。这是psi的第一数值的1倍 ， 是psi的第二数值的0倍 。这等于原始psi的第一个数字 。
通过这些权重 ， 我们有效地切换了psi数值的位置 。
在数学上 ， 这是一个矩阵乘法 。将矩阵M与向量υ相乘的一般公式为：
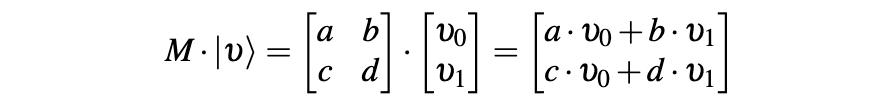作为码农，你无需成为数学家即可掌握量子计算文章插图
a和b是我们用来计算所得向量的第一个数字的权重 。c和d分别是第二个数字的权重 。
数学上 ， X门量子算子是矩阵：
作为码农，你无需成为数学家即可掌握量子计算文章插图
让我们将此运算符应用于我们的三个示例状态：
反转状态|0?将导致|1?：
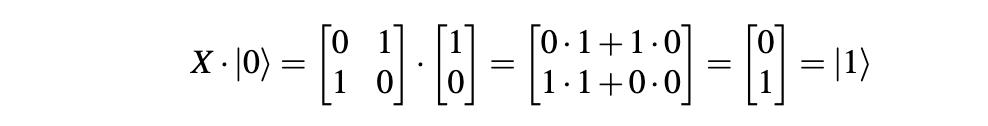作为码农，你无需成为数学家即可掌握量子计算文章插图
反转状态|1?导致|0?：
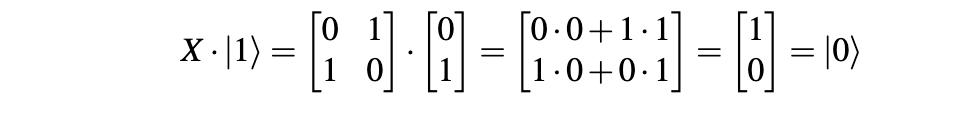作为码农，你无需成为数学家即可掌握量子计算文章插图
而且 ， 在|ψ?处应用矩阵也会导致其反转：
作为码农，你无需成为数学家即可掌握量子计算文章插图
在经典计算中 ， 我们只有一小部分布尔运算符 ， 它们的行为可以很容易地在真值表中表示 。但是在量子计算中 ， 矩阵表示的运算符称为门 。我们可以应用无数种可能的矩阵 。数学是描述这些运算符的简洁而精确的方法 。但是您无需成为数学家即可使用这些运算 。
当然 ， 在您应用门时 ， 需要对门的基础数学有所了解 。但更重要的是 ， 您需要了解门的功能 。如果您知道X门的用途 ， 则无需一直处理数学 。
这篇文章是这本书的一部分：动手使用Python进行量子机器学习 。
作为码农，你无需成为数学家即可掌握量子计算文章插图
在这里免费获取前三章 。
(本文翻译自Frank Zickert的文章《You Don't Need To Be A Mathematician To Master Quantum Computing》 ， 参考：)


推荐阅读


上一篇：教你给手机设置“特效壁纸”，实现桌面分屏

下一篇：PS5官方拆机演示：内部硬件一览无余