江苏龙网

  1. 首页 > 资讯 > 资讯 > >

定义|反向传播算法：定义，概念，可视化( 二 )


我们考虑x的组成，以及它的成分如何影响药物的整体效果。
在这里，我们测量的是整个药物的效果对药物中这个小成分的敏感度。
一个简单的模型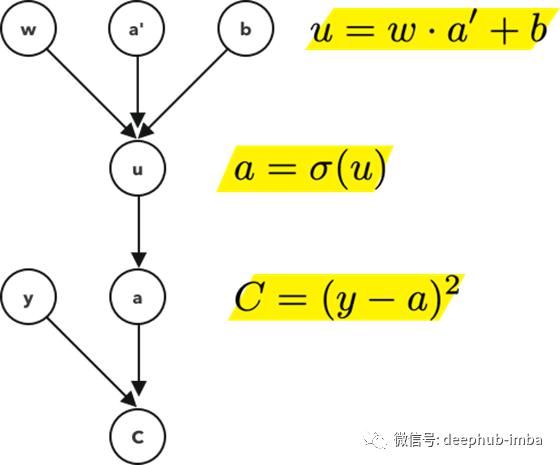
定义|反向传播算法：定义，概念，可视化
文章图片
这个计算图考虑了节点a和它前面的节点a '之间的连接。
用链式法则，
它测量了a对u的微小变化有多敏感。然后我们继续前面的3次计算，
测量u对以下每一项的微小变化的敏感度:
权重,w
之前的激活值，a '
偏质,b
把这些放在一起，
简单模型的复杂性
如果在前面的例子中，我们有两个节点和它们之间的一个链接。在这个例子中，我们有3个节点和2个链接。
因为链式法则的链式长度是没有限制的。我们可以对任意数量的层继续这样做。对于这一层，注意计算图是这样的，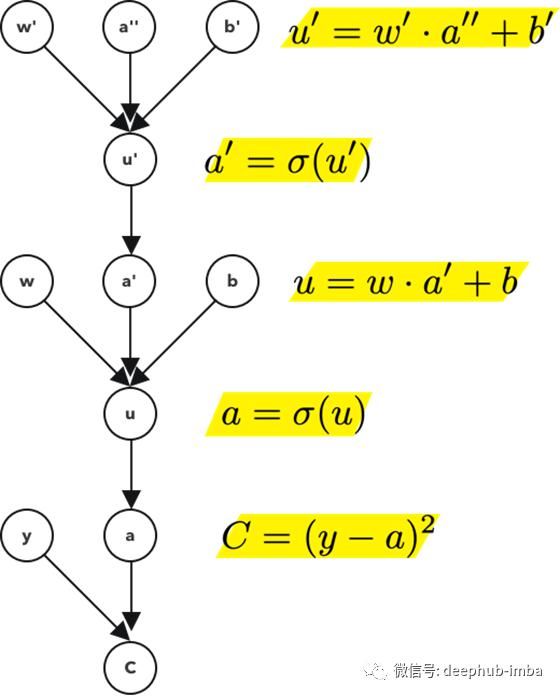
定义|反向传播算法：定义，概念，可视化
文章图片
请注意，需要用附加的刻度对每个节点进行注释。这些刻度不是衍生物，它们只是表示u和u '是不同的、唯一的值或对象
复杂模型的复杂性
到目前为止的例子都是线性的，链表式的神经网络。把它扩展到现实的网络是这样的，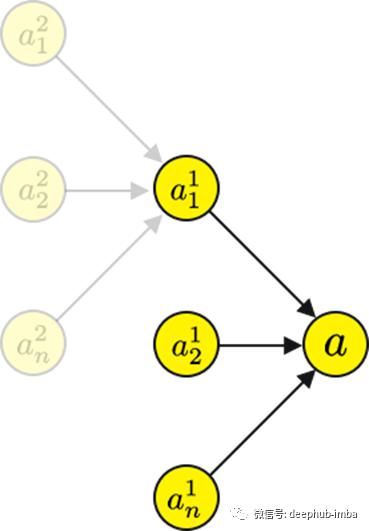
定义|反向传播算法：定义，概念，可视化
文章图片
我们需要给网络添加一些额外的符号。
让我们通过 a1?计算一下计算图 a2?。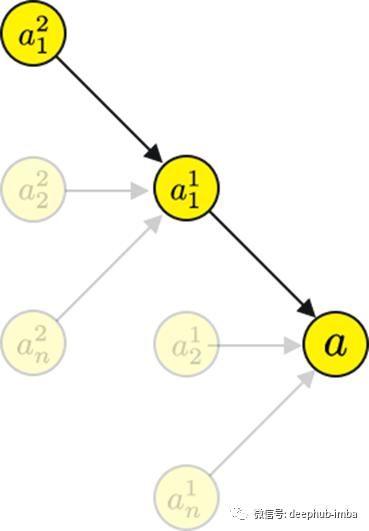
定义|反向传播算法：定义，概念，可视化
文章图片
定义|反向传播算法：定义，概念，可视化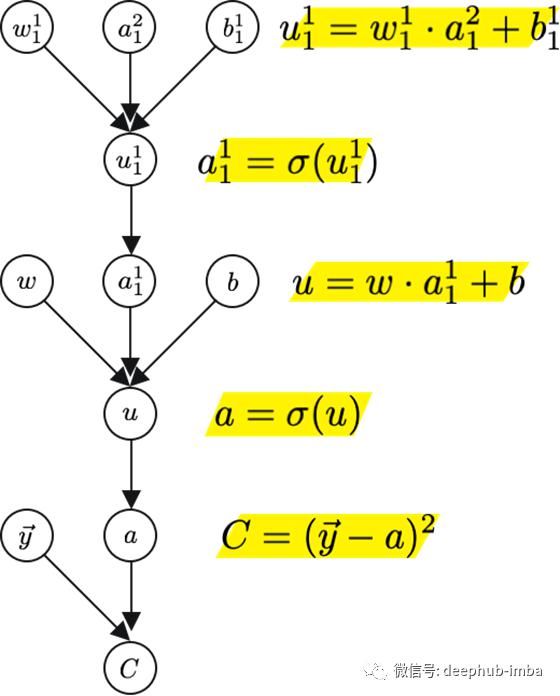
文章图片
实际上你会发现两个计算图有一个很大的共同点,特别是到a1?。这意味着，如果一个计算已经被计算过，那么它可以在下一次和下下次被重用，依此类推。虽然这增加了内存的占用，但它显著减少了计算时间，而且对于大型神经网络来说，这是必要的。
如果我们用链式法则，得到的公式几乎是一样的，只是增加了索引。
复杂模型的进一步复杂化
你会发现一个a2? 会有几个路径输出层节点,。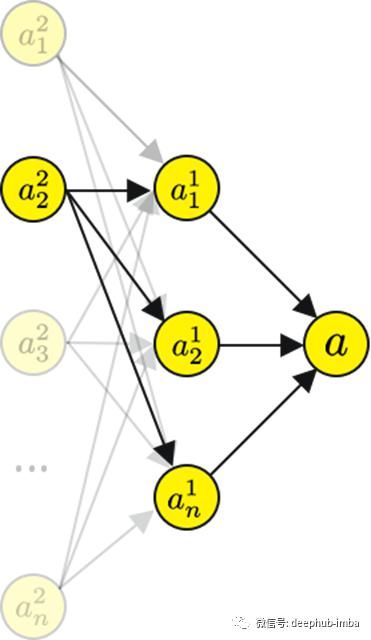
定义|反向传播算法：定义，概念，可视化
文章图片
所以我们需要对前一层求和。我们从所有前面的节点和它们的梯度的总和中得到的这个值有更新它的指令，以便我们最小化损失。
最小化成本函数
如果你还记得定义6和7，特别是定义7，你会记得成本函数在概念上是预测产出和实际产出之差的平均值或加权平均值。
如果我们使用线性回归或逻辑回归的梯度下降算法来最小化代价函数。
对于神经网络，我们使用反向传播算法。我想现在已经很清楚为什么我们不能对神经网络使用单一方程了。神经网络并不是我们可以很好地求导数的连续函数。相反，它们近似一个函数的离散节点。因此需要一个递归算法来找到它的导数或梯度，这需要考虑到所有的节点。
完整的成本函数是这样的:
从概念上讲
符号对符号导数
到目前为止，您已经了解了如何得到神经网络中节点梯度的代数表达式。通过链式法则在张量上的应用和计算图的概念。
代数表达式或计算图不处理具体问题，而只是给我们的理论背景，以验证我们正在正确地计算它们。它们帮助指导我们的编码。
在下一个概念中，我们将讨论符号对数值导数的影响。
符号-数值导数
这里我们开始脱离理论，进入实践领域。
算法
基本设置+计算节点的梯度
首先我们要做一些设置，包括神经网络的顺序以及与网络相关的节点的计算图。我们把它们排列好。
每个节点u^{(n)} 都与一个操作f^{(i)}相关联，使得:
在^ {(i)}是所有节点的集合,u^ {(n)}的父节点。
首先我们需要计算所有的输入节点，为此我们需要将所有的训练数据以x向量的形式输入:
fori=1, ....,n_i
u_i=get_u(x_i)
注意，为输入节点数，其中输入节点为:
如果这些是输入节点，则节点:
是输入节点之后最后一个节点之前的节点u^{(n)}。
fori=n_i+1, ...,n
A_i= {u_j=get_j(Pa(u_i)) }
u_i=fi(A_i)
你会注意到，这和我们链式法则计算图的概念上的方向是相反的。这是因为这部分详细说明了正向传播。
我们称这个图为:
利用这个图，我们可以构造另一个图:
G中的每个节点计算正向图节点u^i，而B中的每个节点使用链式法则计算梯度。
如果你考虑神经网络中的所有节点和连接它们的边，你就能想到反向传播所需的计算量随着边的数量线性增加。因为每条边都代表了一条链规则的计算，它将一些节点连接到它的一个父节点。
附加约束+简单的反向传播
如前所述，该算法的计算复杂度与网络的边数呈线性关系。但这是假设求每条边的偏导数需要一个常数时间。
在这里，我们的目标是建立一个具体反向传播算法。
Run forward propagation
这将获得处于随机的或非有用状态的网络的激活值。
Initialize grad_table
在这个数据结构中，我们将存储所有我们计算的梯度。
To get an individual entry, we use grad_table(u_i)


推荐阅读


上一篇： Store|直播带货坑点多？UB Store破解直播电商四大痛点场景

下一篇： 痴迷|溥仪大婚, 获得一件礼物, 非常痴迷, 为此竟干了一件违背祖制事情