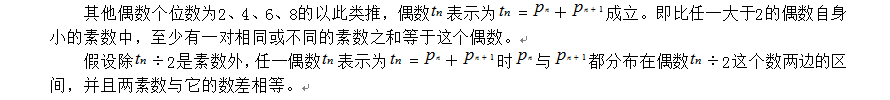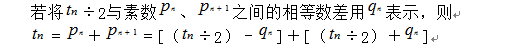дҪң家е”җеӣҪжҳҺз”ЁвҖңдёӘдҪҚеҢәй—ҙжі•вҖқж–°иҜҒе“Ҙеҫ·е·ҙиө«зҢңжғі1пјӢ1и®әж–Үзҡ„2020е№ҙзүҲ вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ” вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”

пјҲжң¬ж–ҮдҪңиҖ…е”җеӣҪжҳҺпјү

вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ” вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ” е”җеӣҪжҳҺи®әиҜҒзҡ„вҖңе“Ҙеҫ·е·ҙиө«зҢңжғі1+1вҖқи®әж–Ү вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ”вҖ” йўҳзӣ®пјҡгҖҠе”җеӣҪжҳҺз”ЁвҖңдёӘдҪҚеҢәй—ҙжі•вҖқж–°иҜҒе“Ҙеҫ·е·ҙиө«зҢңжғі1пјӢ1вҖ”вҖ”д»»дёҖеҒ¶ж•°иЎЁзӨәдёәдёӨзҙ ж•°д№Ӣе’Ңж—¶зҡ„дёҚеҜ№зӯүзҙ ж•°йғҪеҲҶеёғеңЁвҖңеҒ¶ж•°йҷӨд»Ҙ2вҖқдёӨиҫ№зҡ„еҢәй—ҙ пјҢ 并дёҺд№Ӣж•°е·®зӣёзӯүгҖӢ вҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰ ж‘ҳиҰҒпјҡж— и®әдёҖдёӘеӨҡеӨ§зҡ„зҙ ж•° пјҢ йҷӨзҙ ж•°2дёҺ5еӨ– пјҢ е®ғзҡ„дёӘдҪҚж•°жҖ»жҳҜ1гҖҒ3гҖҒ7гҖҒ9пјӣж— и®әеӨҡд№ҲеӨ§еҒ¶ж•° пјҢ е®ғзҡ„дёӘдҪҚж•°жҖ»жҳҜ0гҖҒ2гҖҒ4гҖҒ6гҖҒ8 пјҢ д»»дёҖеҒ¶ж•°иЎЁзӨәдёәдёӨзҙ ж•°д№Ӣе’Ңж—¶зҡ„дёҚеҜ№зӯүзҙ ж•°йғҪеҲҶеёғеңЁвҖңеҒ¶ж•°йҷӨд»Ҙ2вҖқдёӨиҫ№зҡ„еҢәй—ҙ пјҢ 并дёҺд№Ӣж•°е·®зӣёзӯү гҖӮ жҲ–иҜҙ пјҢ жҜҸдёҖдёӘеӨ§дәҺ2зҡ„жӯЈж•ҙж•°йғҪжҳҜдёӨдёӘзҙ ж•°д№Ӣе’Ңзҡ„дёҖеҚҠ пјҢ дё”дёӨдёӘдёҚеҗҢзҡ„зҙ ж•°еҲҶеёғеңЁиҝҷдёӘж•°дёӨиҫ№зҡ„еҢәй—ҙ пјҢ 并дёҺд№Ӣж•°е·®зӣёзӯү гҖӮ иҝҷдёӘзҗҶи®әжҲ‘们еңЁе·ІзҹҘзҡ„еҒ¶ж•°зҙ ж•°еҢәй—ҙжҳҜжҲҗз«Ӣзҡ„ пјҢ йқўеҜ№ж— з©·ж— е°Ҫзҡ„жңӘзҹҘж•°жҲ‘们еҸӘиғҪеңЁдёҖдёӘеҢәй—ҙж•°дёҖдёӘеҢәй—ҙж•°зҡ„жҺЁиҝӣйӘҢиҜҒдёӯи®ӨеҸҜиҝҷдёӘзҗҶи®ә пјҢ еӣ жӯӨе“Ҙеҫ·е·ҙиө«зҢңжғіеҚі

вҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰ е…ій”®иҜҚпјҡдёӘдҪҚ еҢәй—ҙ вҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰ пјҲ1пјүгҖҒеңЁи®әиҜҒиҜҒжҳҺвҖң1пјӢ1вҖқжҲҗз«ӢеүҚжғіиҜҙзҡ„иҜқ вҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰ зңҹзҗҶе°ұз®ҖеҚ•жҳҺдәҶзҡ„ж‘ҶеңЁйӮЈе„ҝ пјҢ еҸӘжҳҜзӯүеҫ…дәәеҺ»еҸ‘зҺ°иҖҢе·І гҖӮ вҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰ пјҲ2пјүгҖҒвҖң1пјӢ1вҖқжҲҗз«Ӣзҡ„зҗҶи®әиҝҮзЁӢ вҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰвҖҰ дёҖдёӘеӨ§дәҺ1зҡ„иҮӘ然数 пјҢ еҰӮжһңдёҚиғҪеңЁ1йҷӨеӨ–зҡ„жғ…еҶөдёӢиў«жҜ”е®ғжң¬иә«е°Ҹзҡ„иҮӘ然数ж•ҙйҷӨ пјҢ йӮЈе®ғе°ұжҳҜдёҖдёӘзҙ ж•° гҖӮ ж №жҚ®дёҚз®ЎеҘҮзҙ ж•°жңүж— йҷҗеӨҡ пјҢ жңүж— з©·еӨ§ пјҢ йҷӨзҙ ж•°5еӨ–жҜҸдёӘеӨ§дәҺ2зҡ„еҘҮзҙ ж•°йғҪйҖғдёҚиҝҮдёӘдҪҚж•°еңЁ1гҖҒ3гҖҒ7гҖҒ9дёӯзҡ„еҫӘзҺҜиҪ¬жҚўжҖ§иҙЁ пјҢ е…¶дёӘдҪҚж•°дёҚз®ЎеҰӮдҪ•дёӨдёӨзӣёеҠ пјҢ еҫ—еҮәзҡ„з»“жһңйғҪеҲҶеҲ«жҳҜдёӘдҪҚж•°еңЁ0гҖҒ2гҖҒ4гҖҒ6гҖҒ8д№Ӣй—ҙеҫӘзҺҜеҸҳеҠЁзҡ„еҒ¶

е°Ҷиҝҷдәӣж•°з»„зӯӣйҖүжЈҖжөӢеҗҺ пјҢ иҝҮе…ізҡ„31гҖҒ89пјӣ41гҖҒ79пјӣ23гҖҒ97пјӣ53гҖҒ67йғҪжҳҜзҙ ж•°пјӣжүҖд»ҘеҒ¶ж•°120еҸҜд»Ҙз”ЁдёӨзҙ ж•°вҖң1пјӢ1вҖқиЎЁзӨәдёәпјҡ 120п№Ұ31пјӢ89п№Ұ41пјӢ79п№Ұ23пјӢ97п№Ұ53пјӢ67пјӣ
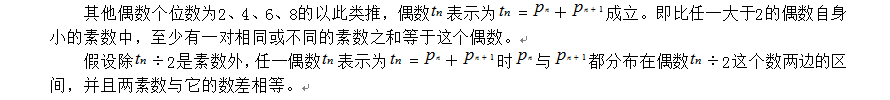
еҰӮеҒ¶ж•°120 пјҢ 120Г·2п№Ұ60 пјҢ иҖҢиЎЁзӨәеҒ¶ж•°120дёәдёӨж•°д№Ӣе’Ңзҡ„зҙ ж•° пјҢ жңү4еҜ№ пјҢ еҚі 120п№Ұ31пјӢ89п№Ұ41пјӢ79п№Ұ23пјӢ97п№Ұ53пјӢ67 е·ІзҹҘ120Г·2п№Ұ60еҲҷ 60п№Ј31п№Ұ89п№Ј60п№Ұ29 60п№Ј41п№Ұ79п№Ј60п№Ұ19 60п№Ј23п№Ұ97п№Ј60п№Ұ17 60п№Ј53п№Ұ67п№Ј60п№Ұ7 еҚі31вҶ’60вҶ’89 пјҢ 41вҶ’60вҶ’79 пјҢ 23вҶ’60вҶ’97 пјҢ 53вҶ’60вҶ’67 пјҢ еҚіеҲҶеёғеңЁ60д№ӢеүҚе°‘дәҺ60еҢәй—ҙзҡ„зҙ ж•° пјҢ дёҺеҲҶеёғеңЁ60д№ӢеҗҺеӨ§дәҺ60зҡ„еҢәй—ҙзҙ ж•°дёӯ пјҢ дёҖеҜ№зӯүдәҺеҒ¶ж•°120зҡ„зҙ ж•°еҜ№ пјҢ дёҺ60зҡ„ж•°е·®зӣёзӯү гҖӮ
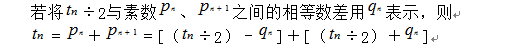
з»ҸдёҠи®әиҜҒжүҖиҝ°еҪ’зәі пјҢ еҸҜеҫ—е®ҡзҗҶпјҡд»»дёҖдёӘеӨ§дәҺ1зҡ„жӯЈж•ҙж•°еҠ еҮҸеҗҢдёҖдёӘжҜ”иҮӘе·ұе°Ҹзҡ„жӯЈж•ҙж•° пјҢ иҮіе°‘иғҪжүҫеҲ°дёҖеҜ№зӣёеҗҢжҲ–дёҚзӣёеҗҢзҡ„зҙ ж•° пјҢ е®ғ们зҡ„е’ҢжҳҜзӯүдәҺиҝҷдёӘж•°иҮӘиә«2еҖҚзҡ„еҒ¶ж•° гҖӮ еӣ жӯӨ пјҢ еҚіжҜ”д»»дёҖеӨ§дәҺ2зҡ„еҒ¶ж•°иҮӘиә«е°Ҹзҡ„зҙ ж•°дёӯиҮіе°‘жңүдёҖеҜ№зӣёеҗҢжҲ–дёҚеҗҢзҡ„зҙ ж•°д№Ӣе’ҢзӯүдәҺиҝҷдёӘеҒ¶ж•° гҖӮ еҰӮжһңдёҖдёӘеҒ¶ж•°дёҚиғҪиЎЁзӨәдёәдёӨзҙ ж•°д№Ӣе’Ң пјҢ йӮЈд№ҲиғҪиЎЁзӨәдёәеҒ¶ж•°зҡ„жүҖжңүеҘҮж•°еҜ№ пјҢ е…ЁжҳҜеҗҲж•° гҖӮ йҖҡиҝҮеүҚйқўи®әиҜҒдёҺдёҫдҫӢиҜҒжҳҺеҫ—зҹҘ пјҢ иҝҷе®ҡзҗҶдёҚжҲҗз«Ӣ гҖӮ еӣ жӯӨ пјҢ дёҖдёӘеҒ¶ж•°иғҪиЎЁзӨәдёәдёӨзҙ ж•°д№Ӣе’Ң гҖӮ дёҖдёӘеҒ¶ж•°и¶ҠеӨ§ пјҢ дёҖдёӘеҒ¶ж•°иғҪиЎЁзӨәжҲҗдёӨдёӘзҙ ж•°д№Ӣе’Ңзҡ„жҰӮзҺҮеҚҙеңЁдёҚж–ӯеўһеӨ§пјӣиҖҢдёҖдёӘеҒ¶ж•°и¶Ҡе°Ҹ пјҢ дёҖдёӘеҒ¶ж•°иғҪиЎЁзӨәжҲҗдёӨдёӘзҙ ж•°д№Ӣе’Ңзҡ„жҰӮзҺҮеҚҙи¶Ҡе°Ҹ гҖӮ ж №жҚ®еҸҜи§Ғзҡ„дәӢзү©и§„еҫӢ пјҢ еҸҜи§ҒдәӢзү©жҳҜжқҘиҮӘдәҺжҲ‘们ж—Ҙеёёйҡҫд»Ҙз©·е°ҪдёҚеҸҜи§Ғзҡ„йғЁеҲҶ规еҫӢдҪңдёәж”Ҝж’‘зҡ„пјӣжҲ‘们иғҪи§Ғзҡ„дәӢзү©и§„еҫӢ пјҢ жқҘиҮӘдәҺдёҚеҸҜи§Ғзҡ„и·қзҰ»жҲ‘们йҒҘиҝңзҡ„дәӢзү©йӮЈдёҖйғЁеҲҶз©ҝи¶Ҡж—¶з©әз”ұиў«йҒ®и”Ҫжј”з»ҺеҲ°жҫ„жҳҺ пјҢ е°Ҷе®ғ们зҡ„规еҫӢе‘ҲзҺ°еңЁжҲ‘们йқўеүҚ гҖӮ жүҖд»ҘжҲ‘们з”ұеҒ¶ж•°4ејҖе§ӢеҺ»жҺЁзҹҘпјҡжҜ”д»»дёҖеӨ§дәҺ2зҡ„еҒ¶ж•°иҮӘиә«е°Ҹзҡ„зҙ ж•°дёӯиҮіе°‘жңүдёҖеҜ№зӣёеҗҢжҲ–дёҚеҗҢзҡ„зҙ ж•°д№Ӣе’ҢиғҪиЎЁзӨәиҝҷдёӘеҒ¶ж•° гҖӮ еҰӮеҒ¶ж•°20д»ҘеүҚеҘҮзҙ ж•°жҳҜ3гҖҒ5гҖҒ7гҖҒ11гҖҒ13гҖҒ17гҖҒ19 пјҢ зҺ°е°Ҷе®ғ们иҪ®жөҒзӣёеҠ пјҢ еҲҷеҸҜеҫ—еҮәзҡ„еҒ¶ж•°жҳҜпјҡ 4гҖҒ6гҖҒ8гҖҒ10гҖҒ12гҖҒ14гҖҒ16гҖҒ18гҖҒ20гҖҒ22гҖҒ24гҖҒ26гҖҒ28гҖҒ30гҖҒ32гҖҒ34гҖҒ36гҖҒ38 е°ҸдәҺеҒ¶ж•°20зҡ„зҙ ж•°дёӯдёӨзҙ ж•°д№Ӣе’ҢйҷӨиғҪиЎЁзӨәеҒ¶ж•°20еүҚзҡ„ж•°еӨ– пјҢ иҝҳиғҪиЎЁзӨәеӨ§дәҺеҒ¶ж•°20д»ҘеҗҺзҡ„9дёӘзӣёйӮ»зҡ„еҒ¶ж•°22гҖҒ24гҖҒ26гҖҒ28гҖҒ30гҖҒ32гҖҒ34гҖҒ36гҖҒ38пјӣеӣ жӯӨеҸҜиӮҜе®ҡиҜҙпјҡдёҖдёӘеҒ¶ж•°и¶ҠеӨ§ пјҢ е®ғеүҚйқўеҢ…еҗ«зҡ„зҙ ж•°е°ұи¶ҠеӨҡ пјҢ дёҖдёӘеҒ¶ж•°иғҪиЎЁзӨәжҲҗдёӨдёӘзҙ ж•°д№Ӣе’Ңзҡ„жҰӮзҺҮд№ҹеңЁдёҚж–ӯеўһеӨ§ гҖӮ ж №жҚ®и®әиҜҒ пјҢ еӣ жӯӨеҚід»»дҪ•дёҖдёӘеӨ§дәҺ2зҡ„еҒ¶ж•° пјҢ еҸҜд»ҘиЎЁзӨәдёәвҖң1пјӢ1вҖқеҫ—иҜҒ гҖӮ е…¶йҖҡз”Ёе…¬ејҸдёәпјҡ
жҺЁиҚҗйҳ…иҜ»
-
гҖҢж—Ҙжң¬гҖҚж—Ҙжң¬жҚЎдәҶдёӘеӨ§дҫҝе®ңпјҒдҝ„зҪ—ж–ҜеҸ–ж¶ҲеҜ№еҚҺи®ўеҚ•пјҢж—Ҙжң¬и¶ҒжңәжӢҝдёӢ150дәҝеӨ§еҚ•
-
гҖҠдёҺеҮӨиЎҢгҖӢдёәдҪ•з¬Ұз”ҹдјҡжӯўж°ҙжңҜпјҹиЎҢжӯўжІЎжғіеҲ°пјҢиҮӘе·ұж—©е°ұиў«з®—и®ЎдәҶ
-
зҪ‘ж–Ү|зҪ‘ж–ҮеңҲ еҗғз“ңзІҫйҖү20жңҹ
-
жҳҺжҳҹзҙ йўң|йҡҫжҖӘе®ҒйқҷиҜҙжҙ—дәҶи„ёйғҪжҳҜй»„и„ёе©ҶпјҢзңӢеҲ°вҖңжөӘе§җвҖқзҙ йўңе·®и·қд№ҹеӨӘеӨ§дәҶеҗ§
-
еҢ—дә¬ж—ҘжҠҘе®ўжҲ·з«Ҝ|еӨ§иҝһпјҡеҜ№дёӨдёӘдёӯйЈҺйҷ©ең°еҢәе…Ёйқўе°Ғй—ӯгҖҒе…Ёйқўж¶ҲжқҖ
-
зү№жң—жҷ®|зү№жң—жҷ®жҢҮиҙЈж°‘дё»е…ҡдәәйҳ»жӯўе»¶з»ӯеӨұдёҡж•‘еҠ©йҮ‘и®ЎеҲ’пјҢжһң然еҸҲйЎәеҳҙз”©й”…дёӯеӣҪ
-
жө·еіЎеҶӣеҝ—|е°„зЁӢ180еҚғзұіпјҢдёӯеӣҪеҸҚиҲ°еҜјеј№жқҘеҲ°зҫҺеӣҪ家门еҸЈпјҒ委еҶ…з‘һжӢүйҮҮиҙӯC-802A
-
зҷҪзҫҠеә§@гҖҗ12жҳҹеә§еҝғзҗҶжөӢйӘҢгҖ‘д»ҺзҲұжғ…и§ӮжөӢеҮәе’ҢдҪ е‘ҪдёӯжіЁе®ҡзҡ„жҒӢдәәжҳҹеә§пјҒ
-
switch|зңҹжңүдҪ зҡ„иҖҒд»»! FCз»Ҹе…ёдҪңе“ҒгҖҠзҒ«з„°зә№з« гҖӢйҷҗж—¶зҷ»йҷҶNS
-
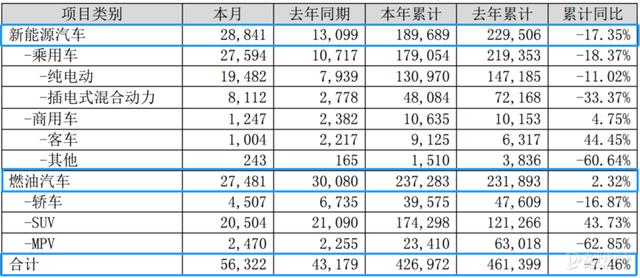
жҜ”дәҡиҝӘ2020е…Ёе№ҙй”ҖйҮҸзәҰ42дёҮиҫҶ еҗҢжҜ”дёӢж»‘7.46%
-
д№°жҲҝзҡ„жөҒзЁӢ иҙӯжҲҝжөҒзЁӢеӣҫ
-
|ејҖе…іжҸ’еә§д»Һ8еқ—еҲ°100еқ—йғҪжңүпјҢ5еҲҶй’ҹи®©жӮЁзҹҘйҒ“йҖүиҙӯж”»з•ҘпјҢи¶…е®һз”Ё
-
еҒҡйҹӯиҸңзӣ’еӯҗзҡ„йқўжҖҺд№Ҳе’Ң йҹӯиҸңзӣ’еӯҗзғ«йқўеҘҪиҝҳжҳҜжӯЈеёёе’Ңйқў
-
зҰҒжҜ’|зҰҒжҜ’иҝӣд№Ўжқ‘ е®Јдј дҝғжҸҗй«ҳ
-
马客иҜҙеҺҶеҸІ|е®Ӣжңқж—¶жңҹзҡ„дёҖдҪҚдёҚиҙҘжҲҳзҘһ,еңЁеңәжҲҳеҪ№дёӯдёҖжҲҳжҲҗеҗҚ
-
еј дё№еі°|жҙӘж¬ЈжҮ’зҗҶе©ҡеҸҳдј й—»дёҺеҘіе„ҝи·іиҲһ иә«жқҗзәӨз»Ҷй•ҝи…ҝжҠўй•ң
-
Autoе®һйӘҢе®Ө|еҘҘеҫ·иөӣи·ҢиҮі19.5дёҮпјҢй…Қйӯ”жңҜй—ЁпјҢиҝҳд№°е•ҘеҲ«е…ӢGL8пјҢжң¬з”°жӢҝеҮәиҜҡж„Ҹ
-
еёёеҗ№ж°ҙзҡ„йҳҝиҜҡ|дјҳеҢ–еҸІиҜ—дёүйҖүдёҖпјҢй”ҷиҝҮз”өзҺ©е°ҸеӯҗжӮ”е“ӯпјҢжІЎзү№е·Ҙзҡ„е·ЁиөҡпјҢзўҺзүҮе•Ҷеә—жӣҙж–°
-
818дҪ“иӮІиө„и®Ҝв– е°Ҹиҙқ1.75дәҝд№°иҝҲйҳҝеҜҶйЎ¶еұӮе…¬еҜ“!жҘјйЎ¶й…ҚзӣҙеҚҮжңәеқӘ,5еҚ§е®ӨдёҖ家6еҸЈжӯЈеҗҲйҖӮ
-
жӢӣиҒҳ|з ”з©¶з”ҹ笔иҜ•з¬¬дёҖпјҢиҝҳжҳҜдёҠеІёеӨұиҙҘпјҢеҜјеёҲжҸӯйңІе…¶еҶ…幕