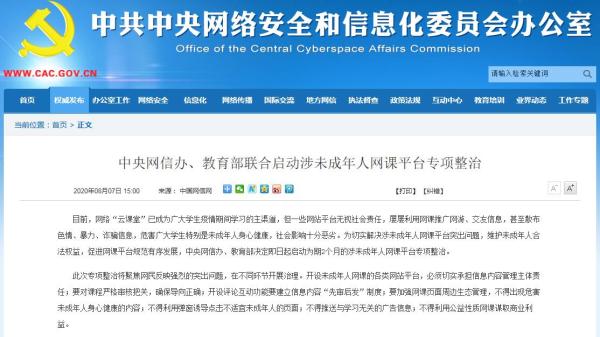
йқ’жңұеҮәе…Ҙеӣҫзҡ„д»Ӣз»Қ йқ’жңұеҮәе…ҘеӣҫиҜҒжі•( дәҢ )
еӨ§ж„ҸжҳҜпјҡдёүи§’еҪўдёәзӣҙи§’дёүи§’еҪўпјҢд»ҘеӢҫaдёәиҫ№зҡ„жӯЈж–№еҪўдёәжңұж–№пјҢд»ҘиӮЎbдёәиҫ№зҡ„жӯЈж–№еҪўдёәйқ’ж–№ гҖӮд»ҘзӣҲиЎҘиҷҡпјҢе°Ҷжңұж–№гҖҒйқ’ж”ҫ并жҲҗејҰж–№ гҖӮдҫқе…¶йқўз§Ҝе…ізі»жңүa^+b^=c^ гҖӮз”ұдәҺжңұж–№гҖҒйқ’ж–№еҗ„жңүдёҖйғЁеҲҶеңЁејҰж–№еҶ…пјҢйӮЈдёҖйғЁеҲҶе°ұдёҚеҠЁдәҶ гҖӮ
д»ҘеӢҫдёәиҫ№зҡ„зҡ„жӯЈж–№еҪўдёәжңұж–№пјҢд»ҘиӮЎдёәиҫ№зҡ„жӯЈж–№еҪўдёәйқ’ж–№ гҖӮд»ҘиөўиЎҘиҷҡпјҢеҸӘиҰҒжҠҠеӣҫдёӯжңұж–№пјҲa2пјүзҡ„I移иҮіIвҖІпјҢйқ’ж–№зҡ„II移иҮіIIвҖІпјҢIII移иҮіIIIвҖІпјҢеҲҷеҲҡеҘҪжӢјеҘҪдёҖдёӘд»ҘејҰдёәиҫ№й•ҝзҡ„жӯЈж–№еҪўпјҲcзҡ„е№іж–№ пјүпјҺз”ұжӯӨдҫҝеҸҜиҜҒеҫ—aзҡ„е№іж–№+bзҡ„е№іж–№=cзҡ„е№іж–№ гҖӮ
иҝҷдёӘиҜҒжҳҺжҳҜз”ұдёүеӣҪж—¶д»ЈйӯҸеӣҪзҡ„ж•°еӯҰ家еҲҳеҫҪжүҖжҸҗеҮәзҡ„ гҖӮеңЁйӯҸжҷҜе…ғеӣӣе№ҙпјҲеҚіе…¬е…ғ 263 е№ҙпјүпјҢеҲҳеҫҪдёәеҸӨзұҚгҖҠд№қз« з®—жңҜгҖӢдҪңжіЁйҮҠ гҖӮеңЁжіЁйҮҠдёӯпјҢд»–з”»дәҶдёҖе№…еғҸеӣҫдә”(b)дёӯзҡ„еӣҫеҪўжқҘиҜҒжҳҺеӢҫиӮЎе®ҡзҗҶ гҖӮ
з”ұж–јд»–еңЁеӣҫдёӯд»ҘгҖҢйқ’еҮәгҖҚгҖҒгҖҢжңұеҮәгҖҚиЎЁзӨәй»„гҖҒзҙ«гҖҒз»ҝдёүдёӘйғЁеҲҶпјҢеҸҲд»ҘгҖҢйқ’е…ҘгҖҚгҖҒгҖҢжңұе…ҘгҖҚи§ЈйҮҠеҰӮдҪ•е°Ҷж–ңиҫ№жӯЈж–№еҪўзҡ„з©әзҷҪйғЁеҲҶеЎ«ж»ЎпјҢжүҖд»ҘеҗҺдё–ж•°еӯҰ家йғҪз§°иҝҷеӣҫдёәгҖҢйқ’жңұе…ҘеҮәеӣҫгҖҚ гҖӮдәҰжңүдәәз”ЁгҖҢеҮәе…ҘзӣёиЎҘгҖҚиҝҷдёҖиҜҚжқҘиЎЁзӨәиҝҷдёӘиҜҒжҳҺзҡ„еҺҹзҗҶ гҖӮ
Q6пјҡйқ’жңұеҮәе…Ҙеӣҫзҡ„д»Ӣз»Қйқ’жңұеҮәе…ҘеӣҫпјҢжҳҜдёңжұүжң«е№ҙж•°еӯҰ家еҲҳеҫҪж №жҚ®вҖңеүІиЎҘжңҜвҖқиҝҗз”Ёж•°еҪўе…ізі»иҜҒжҳҺеӢҫиӮЎе®ҡзҗҶзҡ„еҮ дҪ•иҜҒжҳҺжі•пјҢе…¶жі•еҜҢжңүдёңж–№жҷәж…§пјҢзү№иүІйІңжҳҺгҖҒйҖҡдҝ—жҳ“жҮӮ гҖӮ
е…ідәҺйқ’жңұеҮәе…Ҙеӣҫе’Ңйқ’жңұеҮәе…ҘеӣҫиҜҒжі•зҡ„д»Ӣз»ҚеҲ°жӯӨе°ұз»“жқҹдәҶпјҢдёҚзҹҘйҒ“дҪ д»ҺдёӯжүҫеҲ°дҪ йңҖиҰҒзҡ„дҝЎжҒҜдәҶеҗ—пјҹеҰӮжһңдҪ иҝҳжғідәҶи§ЈжӣҙеӨҡиҝҷж–№йқўзҡ„дҝЎжҒҜпјҢи®°еҫ—收и—Ҹе…іжіЁжң¬з«ҷ гҖӮ
жҹҘзңӢжӣҙеӨҡе…ідәҺйқ’жңұеҮәе…Ҙеӣҫзҡ„иҜҰз»ҶеҶ…е®№...
гҖҗйқ’жңұеҮәе…Ҙеӣҫзҡ„д»Ӣз»Қ йқ’жңұеҮәе…ҘеӣҫиҜҒжі•гҖ‘Tagsпјҡйқ’жңұеҮәе…Ҙеӣҫйқ’жңұеҮәе…ҘеӣҫиҜҒжі•
жҺЁиҚҗйҳ…иҜ»
- еј иүҫеҳү|зҫҺдёҚиҝҮжһ—йқ’йңһпјҢжј”дёҚиҝҮеј жӣјзҺүпјҢжңӘе©ҡз”ҹеӯҗзҡ„еҘ№еҚҙжҙ»жҲҗдәҶдј еҘҮвҖҰ
- иҝҗеҠЁ|43еІҒжұӨе”Ҝй—ӘиҖҖдә®зӣёйҹ©еӣҪйқ’йҫҷеҘ–зәўжҜҜпјҒз©ҝйҰҷеҘҲе„ҝй«ҳе®ҡиөўеҫ—иҪ»жқҫпјҢеӨӘзҫҺдәҶ
- и®ёеҮҜ|и®ёеҮҜгҖҠд»ҷеү‘е…ӯгҖӢжқҖйқ’з…§жӣқе…үпјҒеү‘зңүжҳҹзӣ®йўңеҖјй«ҳпјҢе’Ңиҷһд№Ұж¬ЈеҗҲз…§еҚ–иҗҢпјҒ
- зҲұеҘҮиүәйқ’жҳҘжңүдҪ 2жҖҺд№ҲжҠ•зҘЁ йқ’жҳҘжңүдҪ 2жҠ•зҘЁйҖҡйҒ“
- еҸӨд»Јйқ’й“ңеҷЁзҡ„еҲ¶дҪңж–№жі• йқ’й“ңе·Ҙиүә
- е°ҸзңӢжңұиҠійӣЁпјҒ5е№ҙй•ҝеҗҲеҗҢй”Ғе®ҡе‘Ёй№ҸжҺҘзҸӯдәәпјҢжқңй”ӢдәүеҶ еҰӮиҷҺж·»зҝјпјҢзЁідәҶ
- е·Ұе°Ҹйқ’|вҖңдёӯе№ҙзҫҺеҰҮвҖқе·Ұе°Ҹйқ’пјҡз»ҸеҺҶ6ж®өеҲ»йӘЁй“ӯеҝғзҡ„зҲұжғ…пјҢд»Ҡ45еІҒдҫқж—§еҚ•иә«пјҒ
- 61еІҒеҲҳдҪіе’Ң47еІҒжңұеӘӣеӘӣжҸҗеҗҚйҮ‘йёЎеҘ–пјҢиҝҷдёӘдё–з•ҢзңӢи„ёпјҢжӣҙзңӢжј”жҠҖ
- жңұиҠійӣЁиў«йӘӮжғЁдәҶпјҒеҫҗжқ°йҒӯдёҚе…¬е№іеҫ…йҒҮпјҢйҡҫжҖӘе‘Ёй№ҸдјҡзҰ»йҳҹ
- еј еӣҪиҚЈ|еҪ“е№ҙеј еӣҪиҚЈеңЁжқҖйқ’е®ҙдёҠж‘”й…’жқҜпјҡдҪ иҰҒеҶҚж•ўжү“еҘ№пјҢжҲ‘и®©дҪ еҗғдёҚдәҶе…ңзқҖиө°