数据结构与算法系列 - 深度优先和广度优先本文作者：何建辉（公众号：org_yijiao

文章插图
本文作者：何建辉（公众号：org_yijiaoqian）
前言数据结构与算法系列（完成部分）：

时间复杂度和空间复杂度分析
数组的基本实现和特性
链表和跳表的基本实现和特性
栈、队列、优先队列、双端队列的实现与特性
哈希表、映射、集合的实现与特性
树、二叉树、二叉搜索树的实现与特性
堆和二叉堆的实现和特性
图的实现和特性
递归的实现、特性以及思维要点
分治、回溯的实现和特性
深度优先搜索、广度优先搜索的实现和特性
贪心算法的实现和特性
二分查找的实现和特性
动态规划的实现及关键点
Tire树的基本实现和特性
并查集的基本实现和特性
剪枝的实现和特性
双向BFS的实现和特性
启发式搜索的实现和特性
AVL树和红黑树的实现和特性
位运算基础与实战要点
布隆过滤器的实现及应用
LRU Cache的实现及应用
初级排序和高级排序的实现和特性
字符串算法

PS：大部分已经完成在公众号或者GitHub上，后面陆续会在头条补充链接（不允许有外部链接）
本篇讨论深度优先搜索和广度优先搜索相关内容。
关于搜索 --tt-darkmode-color: #A3A3A3;">对于搜索来说，我们绝大多数情况下处理的都是叫 “所谓的暴力搜索”，或者是说比较简单朴素的搜索，也就是说你在搜索的时候没有任何所谓的智能的情况在里面考虑，很多情况下它做的一件事情就是把所有的结点全部遍历一次，然后找到你要的结果。
基于这样的一个数据结构，如果这个数据结构本身是没有任何特点的，也就是说是一个很普通的树或者很普通的图。那么我们要做的一件事情就是遍历所有的结点。同时保证每个点访问一次且仅访问一次，最后找到结果。
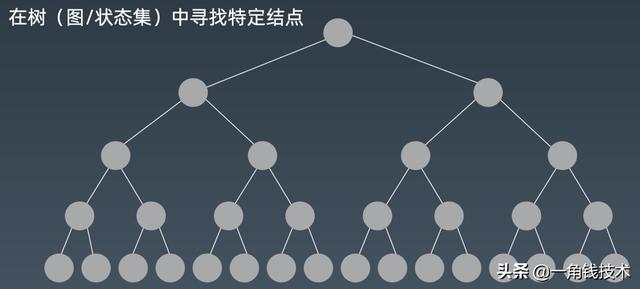
那么我们先把搜索整个先化简情况，我们就收缩到在树的这种情况下来进行搜索。

文章插图
如果我们要找到我们需要的一个值，在这个树里面我们要怎么做？那么毫无疑问就是从根这边开始先搜左子树，然后再往下一个一个一个一个点走过去，然后走完来之后再走右子树，直到找到我们的点，这就是我们所采用的方式。
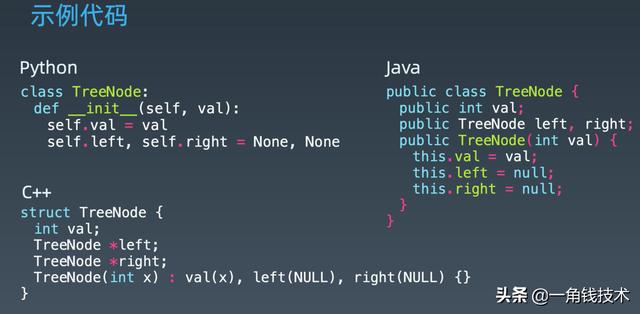
再回到我们数据结构定义，它只有左子树和右子树。

文章插图
我们要实现这样一个遍历或者搜索的话，毫无疑问我们要保证的事情就是

每个结点都要访问一次
每个结点仅仅要访问一次
对于结点访问的顺序不限

深度优先：Depth First Search
广度优先：Breadth First Search

仅访问一次的意思就是代表我们在搜索中，我们不想做过多无用的访问，不然的话我们的访问的效率会非常的慢。
当然的话还可以有其余的搜索，其余的搜索的话就不再是深度优先或者广度优先了，而是按照优先级优先。当然你也可以随意定义，比如说从中间优先类似于其他的东西，但只不过的话你定义的话要有现实中的场景。所以你可以认为是一般来说就是深度优先、广度优先，另外的话就是优先级优先。按照优先级优先搜索的话，其实更加适用于现实中的很多业务场景，而这样的算法我们一般把它称为启发式搜索，更多应用在深度学习领域。而这种比如说优先级优先的话，在很多时候现在已经应用在各种推荐算法和高级的搜索算法，让你搜出你中间最感兴趣的内容，以及每天打开抖音、快手的话就给你推荐你最感兴趣的内容，其实就是这个原因。