数据结构与算法系列 - 深度优先和广度优先( 二 )
深度优先搜索(DFS)递归写法递归的写法 , 一开始就是递归的终止条件 , 然后处理当前的层 , 然后再下转 。
- 那么处理当前层的话就是相当于访问了结点 node , 然后把这个结点 node 加到已访问的结点里面去;
- 那么终止条件的话 , 就是如果这个结点之前已经访问过了 , 那就不管了;
- 那么下转的话 , 就是走到它的子结点 , 二叉树来说的话就是左孩子和右孩子 , 如果是图的话就是连同的相邻结点 , 如果是多叉树的话这里就是一个children,然后把所有的children的话遍历一次 。
- 二叉树模版
//C/C++//递归写法:map visited;void dfs(Node* root) {// terminatorif (!root) return ;if (visited.count(root->val)) {// already visitedreturn ;}visited[root->val] = 1;// process current node here.// ...for (int i = 0; i < root->children.size(); ++i) {dfs(root->children[i]);}return ;} Python 版本#Pythonvisited = set() def dfs(node, visited):if node in visited: # terminator# already visitedreturnvisited.add(node)# process current node here....for next_node in node.children():if next_node not in visited:dfs(next_node, visited)C/C++ 版本//C/C++//递归写法:map visited;void dfs(Node* root) {// terminatorif (!root) return ;if (visited.count(root->val)) {// already visitedreturn ;}visited[root->val] = 1;// process current node here.// ...for (int i = 0; i < root->children.size(); ++i) {dfs(root->children[i]);}return ;} JavaScript版本visited = set() def dfs(node, visited):if node in visited: # terminator# already visitedreturnvisited.add(node)# process current node here....for next_node in node.children():if next_node not in visited:dfs(next_node, visited)- 多叉树模版
visited = set() def dfs(node, visited):if node in visited: # terminator# already visitedreturnvisited.add(node)# process current node here....for next_node in node.children():if next_node not in visited:dfs(next_node, visited)非递归写法Python版本#Pythondef DFS(self, tree):if tree.root is None:return []visited, stack = [], [tree.root]while stack:node = stack.pop()visited.add(node)process (node)nodes = generate_related_nodes(node)stack.push(nodes)# other processing work...C/C++版本//C/C++//非递归写法:void dfs(Node* root) {map visited;if(!root) return ;stack stackNode;stackNode.push(root);while (!stackNode.empty()) {Node* node = stackNode.top();stackNode.pop();if (visited.count(node->val)) continue;visited[node->val] = 1;for (int i = node->children.size() - 1; i >= 0; --i) {stackNode.push(node->children[i]);}}return ;} 遍历顺序我们看深度优先搜索或者深度优先遍历的话 , 它的整个遍历顺序毫无疑问根节点 1 永远最先开始的 , 接下来往那个分支走其实都一样的 , 我们简单起见就是从最左边开始走 , 那么它深度优先的话就会走到底 。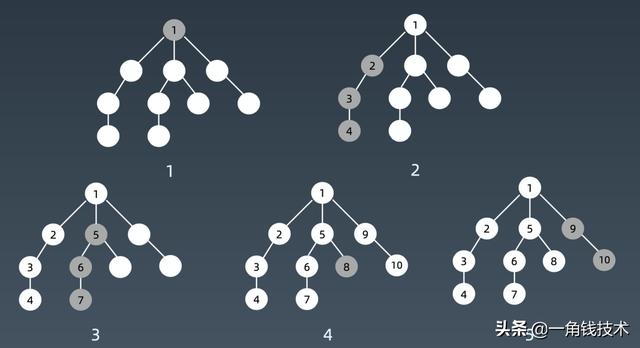 文章插图
文章插图参考多叉树模版我们可以在脑子里面或者画一个图把它递归起来的话 , 把递归的状态树画出来 , 就是这么一个结构 。
推荐阅读
- 三星新旗舰Galaxy S21系列发布倒计时3天
- 改变网络化办公 揭秘夏普新复合机系列
- 网络双面提速办公 夏普发布全新复印机系列
- 向日葵远程控制企业版客户端更新升级,优化远控UI适配SADDC内核算法
- 电脑报2020年度获奖产品:引领智能商务无线投影时代的明基E系列商务投影机
- 手机必须双扬声器 魅族17系列告诉你这不是噱头
- 三星S21系列再次3C认证 充电器或成为“可选”配件
- 三星竟为Galaxy S21系列提供900多种颜色配置
- 摩托罗拉发布2021款Moto G系列产品 内建大容量电池169美元起价
- 影像旗舰vivo X60系列正式开售 斩获多个线上平台双冠军














