1Tж•°жҚ®еҝ«йҖҹжҺ’еәҸпјҒеҚҒз§Қз»Ҹе…ёжҺ’еәҸз®—жі•жҖ»з»“( дёү )
еҗҲ并зҡ„иҝҮзЁӢжҳҜе°ҶдёӨдёӘжҢҮй’ҲжҢҮеҗ‘дёӨдёӘеӯҗж•°з»„зҡ„йҰ–дҪҚе…ғзҙ пјҢ дёӨдёӘе…ғзҙ иҝӣиЎҢжҜ”иҫғ пјҢ иҫғе°Ҹзҡ„жҸ’е…ҘеҲ°дёҖдёӘtempж•°з»„дёӯ пјҢ еҗҢж—¶е°ҶиҜҘж•°з»„зҡ„жҢҮй’ҲеҸіз§»дёҖдҪҚ пјҢ 继з»ӯжҜ”иҫғиҜҘж•°з»„зҡ„第дәҢдёӘе…ғзҙ е’ҢеҸҰдёҖдёӘе…ғзҙ вҖҰйҮҚеӨҚиҝҷдёӘиҝҮзЁӢ гҖӮ иҝҷж ·tempж•°з»„дҝқеӯҳзҡ„дҫҝжҳҜиҝҷдёӨдёӘеӯҗж•°з»„жҺ’еҘҪеәҸзҡ„з»“жһң гҖӮ жңҖеҗҺе°Ҷtempж•°з»„еӨҚеҲ¶еӣһеҺҹж•°з»„зҡ„дҪҚзҪ®еӨ„еҚіеҸҜ гҖӮ
public int[] mergeSort(int[] array) {if (array == null || array.length < 2) {return array;}return mergeSort(array, 0, array.length - 1);}private int[] mergeSort(int[] array, int left, int right) {if (left < right) {//иҝҷйҮҢжІЎжңүйҖүжӢ©вҖң(left + right) / 2вҖқзҡ„ж–№ејҸ пјҢ жҳҜдёәдәҶйҳІжӯўж•°жҚ®жәўеҮәint mid = left + ((right - left) >>> 1);// жӢҶеҲҶеӯҗж•°з»„mergeSort(array, left, mid);mergeSort(array, mid + 1, right);// еҜ№еӯҗж•°з»„иҝӣиЎҢеҗҲ并merge(array, left, mid, right);}return array;}private void merge(int[] array, int left, int mid, int right) {int[] temp = new int[right - left + 1];// p1е’Ңp2дёәйңҖиҰҒеҜ№жҜ”зҡ„дёӨдёӘж•°з»„зҡ„жҢҮй’Ҳ пјҢ kдёәеӯҳж”ҫtempж•°з»„зҡ„жҢҮй’Ҳint p1 = left, p2 = mid + 1, k = 0;while (p1 <= mid} else {temp[k++] = array[p2++];}}// жҠҠеү©дҪҷзҡ„ж•°з»„зӣҙжҺҘж”ҫеҲ°tempж•°з»„дёӯwhile (p1 <= mid) {temp[k++] = array[p1++];}while (p2 <= right) {temp[k++] = array[p2++];}// еӨҚеҲ¶еӣһеҺҹж•°з»„for (int i = 0; i < temp.length; i++) {array[i + left] = temp[i];}}7 еҝ«йҖҹжҺ’еәҸеҝ«йҖҹжҺ’еәҸзҡ„ж ёеҝғжҳҜиҰҒжңүдёҖдёӘеҹәеҮҶж•°жҚ®temp пјҢ дёҖиҲ¬еҸ–ж•°з»„зҡ„第дёҖдёӘдҪҚзҪ®е…ғзҙ гҖӮ 然еҗҺйңҖиҰҒжңүдёӨдёӘжҢҮй’Ҳleftе’Ңright пјҢ еҲҶеҲ«жҢҮеҗ‘ж•°з»„зҡ„第дёҖдёӘе’ҢжңҖеҗҺдёҖдёӘе…ғзҙ гҖӮ
йҰ–е…Ҳд»ҺrightејҖе§Ӣ пјҢ жҜ”иҫғrightдҪҚзҪ®е…ғзҙ е’ҢеҹәеҮҶж•°жҚ® гҖӮ еҰӮжһңеӨ§дәҺзӯүдәҺ пјҢ еҲҷе°ҶrightжҢҮй’Ҳе·Ұ移 пјҢ жҜ”иҫғдёӢдёҖдҪҚе…ғзҙ пјӣеҰӮжһңе°ҸдәҺ пјҢ е°ұе°ҶrightжҢҮй’ҲеӨ„ж•°жҚ®иөӢз»ҷleftжҢҮй’ҲеӨ„пјҲжӯӨж—¶leftжҢҮй’ҲеӨ„ж•°жҚ®е·Ідҝқеӯҳиҝӣtempдёӯпјү пјҢ leftжҢҮй’Ҳ+1 пјҢ д№ӢеҗҺејҖе§ӢжҜ”иҫғleftжҢҮй’ҲеӨ„ж•°жҚ® гҖӮ
жӢҝleftдҪҚзҪ®е…ғзҙ е’ҢеҹәеҮҶж•°жҚ®иҝӣиЎҢжҜ”иҫғ гҖӮ еҰӮжһңе°ҸдәҺзӯүдәҺ пјҢ еҲҷе°ҶleftжҢҮй’ҲеҸіз§» пјҢ жҜ”иҫғдёӢдёҖдҪҚе…ғзҙ пјӣиҖҢеҰӮжһңеӨ§дәҺе°ұе°ҶleftжҢҮй’ҲеӨ„ж•°жҚ®иөӢз»ҷrightжҢҮй’ҲеӨ„ пјҢ rightжҢҮй’Ҳ-1 пјҢ д№ӢеҗҺејҖе§ӢжҜ”иҫғrightжҢҮй’ҲеӨ„ж•°жҚ®вҖҰйҮҚеӨҚиҝҷдёӘиҝҮзЁӢ гҖӮ
зӣҙеҲ°leftе’ҢrightжҢҮй’Ҳзӣёзӯүж—¶ пјҢ иҜҙжҳҺиҝҷдёҖж¬ЎжҜ”иҫғиҝҮзЁӢе®ҢжҲҗ гҖӮ жӯӨж—¶е°Ҷе…ҲеүҚеӯҳж”ҫиҝӣtempдёӯзҡ„еҹәеҮҶж•°жҚ®иөӢеҖјз»ҷеҪ“еүҚleftе’ҢrightжҢҮй’Ҳе…ұеҗҢжҢҮеҗ‘зҡ„дҪҚзҪ®еӨ„ пјҢ еҚіеҸҜе®ҢжҲҗиҝҷдёҖж¬ЎжҺ’еәҸж“ҚдҪң гҖӮ
д№ӢеҗҺйҖ’еҪ’жҺ’еәҸеҹәзЎҖж•°жҚ®зҡ„е·ҰеҚҠйғЁеҲҶе’ҢеҸіеҚҠйғЁеҲҶ пјҢ йҖ’еҪ’зҡ„иҝҮзЁӢе’ҢдёҠйқўи®Іиҝ°зҡ„иҝҮзЁӢжҳҜдёҖж ·зҡ„ пјҢ еҸӘдёҚиҝҮж•°з»„иҢғеӣҙдёҚеҶҚжҳҜеҺҹжқҘзҡ„е…ЁйғЁж•°з»„дәҶ пјҢ иҖҢжҳҜзҺ°еңЁзҡ„е·ҰеҚҠйғЁеҲҶжҲ–еҸіеҚҠйғЁеҲҶ гҖӮ еҪ“е…ЁйғЁзҡ„йҖ’еҪ’иҝҮзЁӢз»“жқҹеҗҺ пјҢ жңҖз»Ҳз»“жһңеҚідёәжҺ’еҘҪеәҸзҡ„з»“жһң гҖӮ
еҝ«йҖҹжҺ’еәҸжү§иЎҢзӨәж„Ҹеӣҫпјҡ
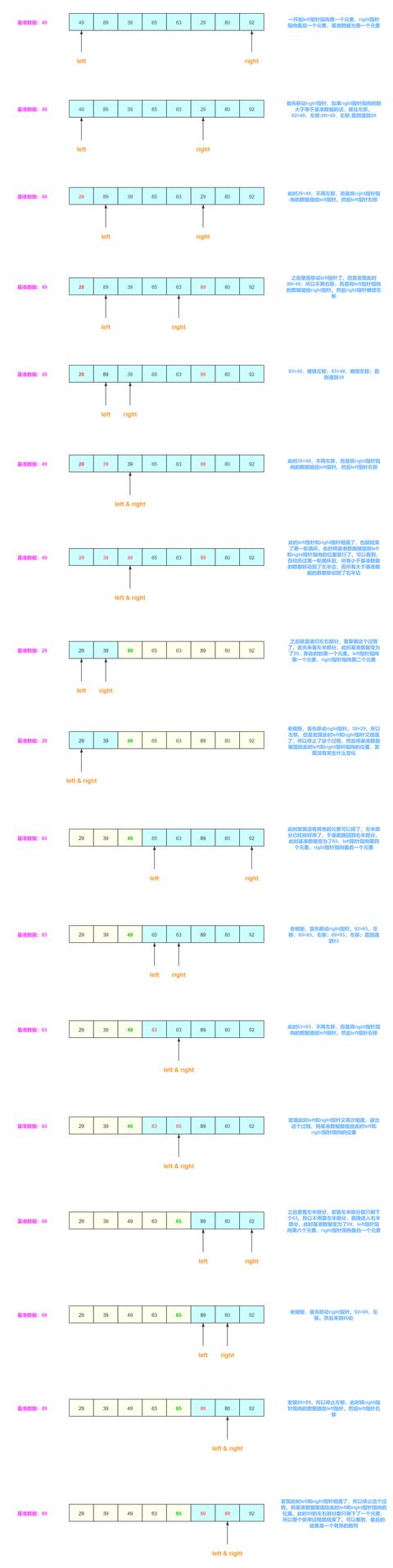 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
жӯЈеҰӮдёҠйқўжүҖиҜҙзҡ„ пјҢ дёҖиҲ¬еҸ–第дёҖдёӘе…ғзҙ дҪңдёәеҹәеҮҶж•°жҚ® пјҢ дҪҶеҰӮжһңеҪ“еүҚж•°жҚ®дёәд»ҺеӨ§еҲ°е°ҸжҺ’еҲ—еҘҪзҡ„ж•°жҚ® пјҢ иҖҢзҺ°еңЁиҰҒжҢүд»Һе°ҸеҲ°еӨ§зҡ„йЎәеәҸжҺ’еҲ— пјҢ еҲҷж•°жҚ®еҲҶж‘ҠдёҚеқҮеҢҖ пјҢ ж—¶й—ҙеӨҚжқӮеәҰдјҡйҖҖеҢ–дёә
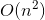 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҢ иҖҢдёҚжҳҜжӯЈеёёжғ…еҶөдёӢзҡ„
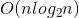 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
гҖӮ жӯӨж—¶йҮҮеҸ–дёҖдёӘдјҳеҢ–жүӢж®ө пјҢ еҚіеҸ–жңҖе·Ұиҫ№гҖҒжңҖеҸіиҫ№е’ҢжңҖдёӯй—ҙзҡ„дёүдёӘе…ғзҙ зҡ„дёӯй—ҙеҖјдҪңдёәеҹәеҮҶж•°жҚ® пјҢ д»ҘжӯӨжқҘйҒҝе…Қж—¶й—ҙеӨҚжқӮеәҰдёә
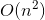 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
зҡ„жғ…еҶөеҮәзҺ° пјҢ еҪ“然д№ҹеҸҜд»ҘйҖүжӢ©жӣҙеӨҡзҡ„й”ҡзӮ№жҲ–иҖ…йҡҸжңәйҖүжӢ©зҡ„ж–№ејҸжқҘиҝӣиЎҢйҖүеҸ– гҖӮ
иҝҳжңүдёҖдёӘдјҳеҢ–зҡ„ж–№жі•жҳҜпјҡеғҸеҝ«йҖҹжҺ’еәҸгҖҒеҪ’并жҺ’еәҸиҝҷж ·зҡ„еӨҚжқӮжҺ’еәҸж–№жі•еңЁж•°жҚ®йҮҸеӨ§зҡ„жғ…еҶөдёӢжҳҜжҜ”йҖүжӢ©жҺ’еәҸгҖҒеҶ’жіЎжҺ’еәҸе’ҢжҸ’е…ҘжҺ’еәҸзҡ„ж•ҲзҺҮиҰҒй«ҳзҡ„ пјҢ дҪҶжҳҜеңЁж•°жҚ®йҮҸе°Ҹзҡ„жғ…еҶөдёӢеҸҚиҖҢиҰҒжӣҙж…ў гҖӮ жүҖд»ҘжҲ‘们еҸҜд»ҘйҖүе®ҡдёҖдёӘйҳҲеҖј пјҢ иҝҷйҮҢйҖүжӢ©дёә47пјҲе’Ңжәҗз ҒдёӯдҪҝз”Ёзҡ„дёҖж ·пјү гҖӮ еҪ“йңҖиҰҒжҺ’еәҸзҡ„ж•°жҚ®йҮҸе°ҸдәҺ47ж—¶иө°жҸ’е…ҘжҺ’еәҸ пјҢ еӨ§дәҺ47еҲҷиө°еҝ«йҖҹжҺ’еәҸ гҖӮ
жҺЁиҚҗйҳ…иҜ»
- иҘҝйғЁж•°жҚ®еңЁCES 2021жҺЁеҮәеӨҡж¬ҫ4TBе®№йҮҸзҡ„ж——иҲ°зә§SSD
- WhatsApp收йӣҶз”ЁжҲ·ж•°жҚ®ж–°ж”ҝжғ№дј—жҖ’пјҢвҖңеҲ йҷӨWhatsAppвҖқеңЁеңҹиҖіе…¶дёҠзғӯжҗң
- вҖңеҚғеә—еҗҢејҖвҖқеј•иҙЁйҮҸжӢ…еҝ§пјҢе°Ҹзұіеӣһеә”
- жңӘжқҘжғіиҝӣе…ҘAIйўҶеҹҹпјҢиҜҘеӯҰд№ PythonиҝҳжҳҜJavaеӨ§ж•°жҚ®ејҖеҸ‘
- дјҒдёҡ|жҠҖжңҜеҝ«йҖҹиҝӯд»ЈеҖ’йҖјзҹҘиҜҶдә§жқғвҖңиҙҙиә«вҖқжңҚеҠЎпјҢдёҠжө·йҰ–家AIе•Ҷж Үе“ҒзүҢжҢҮеҜјз«ҷе…Ҙй©»еҫҗжұҮиҘҝеІё
- й»‘е®ўзӘғеҸ–250дёҮдёӘдәәж•°жҚ® ж„ҸеӨ§еҲ©иҝҗиҗҘе•ҶжҸҗйҶ’з”ЁжҲ·е°Ҫеҝ«жӣҙжҚўSIMеҚЎ
- йҳізӢ®жҠҘе‘Ҡпјҡ4жҲҗеҸ—и®ҝиҖ…и®ӨдёәиҮӘе·ұзҡ„ж•°жҚ®жҜ”е…Қиҙ№жңҚеҠЎжӣҙжңүд»·еҖј
- дёӯж¶ҲеҚҸзӮ№еҗҚеӨ§ж•°жҚ®зҪ‘з»ңжқҖзҶҹ еҸҚеҜ№еҲ©з”Ёж¶Ҳиҙ№иҖ…дёӘдәәж•°жҚ®з”»еғҸ
- еӯҰд№ еӨ§ж•°жҚ®жҳҜеҗҰйңҖиҰҒеӯҰд№ JavaEE
- ж„ҸеӨ§еҲ©иҝҗиҗҘе•ҶHo Mobileиў«жӣқж•°жҚ®жі„йңІ













