жӯЈеҚҒдәҢйқўдҪ“|з”ҹжҙ»еңЁжӯЈеҚҒдәҢйқўдҪ“жҳҹзҗғдёҠзҡ„зӨҫжҒҗеҰӮдҪ•еҲ¶е®ҡж•ЈжӯҘи®ЎеҲ’
д»ҠеӨ© пјҢ и®©жҲ‘们е…Ҳд»ҺдёҖеҲҷзү№ж®Ҡзҡ„вҖқз«ҘиҜқвҖңж•…дәӢејҖе§Ӣпјҡ
еңЁдёҖдёӘжӯЈеӣӣйқўдҪ“жҳҹзҗғзҡ„дёҖдёӘйЎ¶зӮ№дёҠ пјҢ дҪҸзқҖдёҖдҪҚж•°еӯҰ家 пјҢ еңЁиҝҷйў—жҳҹзҗғзҡ„е…¶дҪҷйЎ¶зӮ№дёҠ пјҢ еҗ„жңүдёҖжһқзҺ«з‘° гҖӮ ж•°еӯҰ家жңүдёҖеҸӘзҫҠ пјҢ жҜҸеӨ©д»–йғҪдјҡеёҰзҫҠж•ЈжӯҘ пјҢ д»–дёҚжғіиҪ¬ејҜеҸӘжғіиө°зӣҙзәҝ пјҢ дё”дёҚжғіз»ҸиҝҮе…¶д»–йЎ¶зӮ№ пјҢ е…Қеҫ—зҫҠдјҡеҗғжҺүйӮЈйҮҢзҡ„зҺ«з‘° гҖӮ иҜ·й—®пјҡжңүжІЎжңүиҝҷж ·дёҖжқЎж•ЈжӯҘи·Ҝеҫ„ пјҢ еҸҜд»Ҙи®©ж•°еӯҰ家зҡ„зҫҠжІҝзқҖзӣҙзәҝеҮәеҸ‘еҗҺ пјҢ ж—ўдёҚдјҡз ҙеқҸзҺ«з‘° пјҢ иҝҳиғҪеңЁе®үе…Ёиҝ”еӣһ家дёӯпјҹ
еҰӮжһңдҪ дёҚзҹҘйҒ“й—®йўҳзҡ„зӯ”жЎҲ пјҢ иҜ·е…ҲеҲ«зқҖжҖҘ пјҢ еҶҚжқҘзңӢиҝҷдёӘпјҡ
еңЁдёҖдёӘжӯЈеҚҒдәҢйқўдҪ“жҳҹзҗғзҡ„дёҖдёӘйЎ¶зӮ№дёҠ пјҢ дҪҸзқҖдёҖдҪҚдёҚзҲұзӨҫдәӨзҡ„ж•°еӯҰ家 пјҢ еңЁжҳҹзҗғзҡ„е…¶д»–йЎ¶зӮ№дёҠ пјҢ д№ҹйғҪеҗ„жңүдёҖ家дҪҸжҲ· гҖӮ жҜҸеҪ“ж•°еӯҰ家жғіеҮәеҺ»ж•ЈжӯҘж—¶ пјҢ жҖ»жҳҜе®іжҖ•дјҡз»ҸиҝҮе…¶д»–дҪҸжҲ·зҡ„家иҖҢдёҺд»–дәәзў°йқў гҖӮ еӣ жӯӨд»–ејҖе§ӢдёәиҮӘе·ұи®ҫи®Ўи·ҜзЁӢ пјҢ жғіиҰҒжүҫеҲ°иҝҷж ·дёҖжқЎзӣҙзәҝи·Ҝеҫ„ пјҢ еҸҜд»ҘеңЁж—ўдёҚз»ҸиҝҮеҲ«дәәзҡ„家 пјҢ иҝҳеҸҜд»Ҙиҝ”еӣһеҲ°иҮӘе·ұ家дёӯпјҹ
иҝҷдёӨдёӘй—®йўҳеҗ¬иө·жқҘдјјд№ҺеҫҲеғҸ пјҢ дҪҶе®ғ们жҳҜеҗҰжңүзқҖзӣёеҗҢзҡ„зӯ”жЎҲпјҹ
е…¶е®һ пјҢ жҲ‘们д»ҠеӨ©иҰҒи®Ізҡ„ пјҢ жӯЈжҳҜеҮ дҪҚж•°еӯҰ家 пјҢ еҜ№дәҺеҸ‘з”ҹеңЁиҝҷдәӣвҖқеҘҮжҖӘжҳҹзҗғвҖңдёҠзҡ„вҖқеҘҮжҖӘзҡ„ж•ЈжӯҘйңҖжұӮвҖңй—®йўҳзҡ„з ҙи§Ј гҖӮ
жң¬ж–ҮеӣҫзүҮ
жӯЈдёүи§’еҪўгҖҒжӯЈж–№еҪўгҖҒжӯЈдә”иҫ№еҪўзӯүеӣҫжЎҲ пјҢ жҲ–и®ёжҳҜжҲ‘们еңЁеӯҰж ЎжҺҘи§ҰеҲ°зҡ„жңҖж—©зҡ„еҮ дҪ•еҪўзҠ¶ гҖӮ зҗҶи®әдёҠи®І пјҢ иҝҷз§ҚжҜҸжқЎиҫ№зҡ„й•ҝеәҰгҖҒжҜҸдёӘи§’зҡ„еӨ§е°ҸйғҪзӣёзӯүзҡ„дәҢз»ҙжӯЈеӨҡиҫ№еҪўеҸҜд»Ҙжңүж— з©·еӨҡдёӘ пјҢ еҸӘжҳҜйҡҸзқҖж•°еӯ—зҡ„еўһеӨ§ пјҢ е®ғ们и¶ҠжқҘи¶ҠжҺҘиҝ‘дәҺдёҖдёӘеңҶ гҖӮ
жң¬ж–ҮеӣҫзүҮ
дҪҶжҳҜеҪ“д»ҺдәҢз»ҙжҸҗеҚҮеҲ°дёүз»ҙи°Ҳи®әжӯЈеӨҡйқўдҪ“ж—¶ пјҢ зӣёзӯүзҡ„жҖ§иҙЁйҷӨдәҶиҫ№е’Ңи§’д№ӢеӨ– пјҢ жӯЈеӨҡйқўдҪ“дёҠзҡ„жҜҸдёӘйқўд№ҹеҝ…йЎ»йғҪзӣёзӯү гҖӮ дёҺжӯЈеӨҡиҫ№еҪўдёҚеҗҢзҡ„жҳҜ пјҢ жӯЈеӨҡйқўдҪ“зҡ„з§Қзұ»е№¶дёҚжҳҜж— з©·еӨҡдёӘ пјҢ иҖҢжҳҜжңҖз»ҲеҸҜиў«еҲҶдёәдә”з§ҚпјҡжӯЈеӣӣйқўдҪ“гҖҒз«Ӣж–№дҪ“гҖҒе…«йқўдҪ“гҖҒдәҢеҚҒйқўдҪ“е’ҢеҚҒдәҢйқўдҪ“ гҖӮ
жң¬ж–ҮеӣҫзүҮ
ж— и®әеңЁж•°еӯҰиҝҳжҳҜеңЁиүәжңҜдёҠ пјҢ иҝҷдәӣжӯЈеӨҡйқўдҪ“йғҪжү®жј”дәҶйҮҚиҰҒи§’иүІ гҖӮ дәәзұ»еҜ№жӯЈеӨҡйқўдҪ“зҡ„з ”з©¶е·Із»ҸжҢҒз»ӯдәҶиҮіе°‘дёӨеҚғеӨҡе№ҙ пјҢ 然иҖҢеңЁж•°еӯҰ家зңјдёӯ пјҢ иҝҷдәӣеҮ дҪ•з»“жһ„д»ҚеӯҳеңЁи®ёеӨҡжңӘзҹҘй—®йўҳ пјҢ 并жҖ»иғҪд»Һиҝҷдәӣзү№ж®Ҡзҡ„з»“жһ„дёӯеҸ‘зҺ°дёҖдәӣвҖңж–°йІңдәӢвҖқ гҖӮ
ж•°еӯҰ家Jayadev AthreyaдёҺд»–зҡ„еҗҢдәӢе°ұеҜ№з ”究жӯЈеӨҡйқўдҪ“йқһеёёзғӯиЎ· пјҢ иҮӘ2016е№ҙејҖе§Ӣз ”з©¶д»ҘжқҘ пјҢ 他们已з»ҸжҸҗеҮәдәҶдёҖдәӣж–°зҡ„жғіжі• пјҢ 并еҸ‘зҺ°дәҶдёҖдәӣж–°зҡ„е®ҡзҗҶ гҖӮ дёҚд»…еҰӮжӯӨ пјҢ Athreyaзӯүдәәиҝҳи§ЈеҶідәҶдёҖдёӘе·Із»Ҹеӣ°жү°дәҶж•°еӯҰ家дёҖдёӘеӨҡдё–зәӘд№Ӣд№…зҡ„й—®йўҳ пјҢ иҝҷжҳҜдёҖдёӘе…ідәҺжӯЈеҚҒдәҢйқўдҪ“зҡ„жңҖеҹәжң¬зҡ„й—®йўҳ гҖӮ д»Ҡе№ҙ5жңҲ пјҢ 他们е°Ҷз»“жһңеҸ‘иЎЁеңЁдәҶгҖҠе®һйӘҢж•°еӯҰгҖӢжқӮеҝ—дёҠ гҖӮ
жң¬ж–ҮеӣҫзүҮ
AthreyaжүҖз ”з©¶зҡ„й—®йўҳ пјҢ жӯЈе’Ңж–Үз« ејҖеӨҙзҡ„дёӨеҲҷвҖңз«ҘиҜқвҖқжңүе…і пјҢ еҚіеҒҮеҰӮжҲ‘们з”ҹжҙ»еңЁдёҖдёӘжӯЈеӨҡйқўдҪ“дё–з•Ң пјҢ жңүжІЎжңүеҸҜиғҪеӯҳеңЁиҝҷж ·зҡ„зӣҙзәҝи·Ҝеҫ„ пјҢ еҸҜд»Ҙи®©дҪ д»ҺжӯЈеӨҡйқўдҪ“зҡ„жҹҗдёӘйЎ¶зӮ№еҮәеҸ‘ пјҢ йЎәзқҖиҝҷжқЎзӣҙзәҝдёҖзӣҙеүҚиЎҢ пјҢ еҸҜд»ҘеңЁдёҚз»ҸиҝҮе…¶д»–д»»дҪ•йЎ¶зӮ№зҡ„жғ…еҶөдёӢ пјҢ иҝ”еӣһеҲ°еҺҹзӮ№ гҖӮ
еңЁз ”究жӯЈеӨҡйқўдҪ“зҡ„иҝҷз§Қзӣҙзәҝи·Ҝз»Ҹй—®йўҳж—¶ пјҢ ж•°еӯҰ家дјҡз”ЁеҲ°зҡ„дёҖдёӘеҹәжң¬жғіжі•е°ұжҳҜе°ҶиҝҷдәӣеӨҡйқўдҪ“еұ•ејҖ гҖӮ д»ҘжӯЈеӣӣйқўдҪ“дёәдҫӢ пјҢ е®ғзҡ„еұ•ејҖжҳҜдёҖдёӘз”ұ4дёӘдёүи§’еҪўз»„жҲҗзҡ„зӯүиҫ№дёүи§’еҪў гҖӮ
гҖҗжӯЈеҚҒдәҢйқўдҪ“|з”ҹжҙ»еңЁжӯЈеҚҒдәҢйқўдҪ“жҳҹзҗғдёҠзҡ„зӨҫжҒҗеҰӮдҪ•еҲ¶е®ҡж•ЈжӯҘи®ЎеҲ’гҖ‘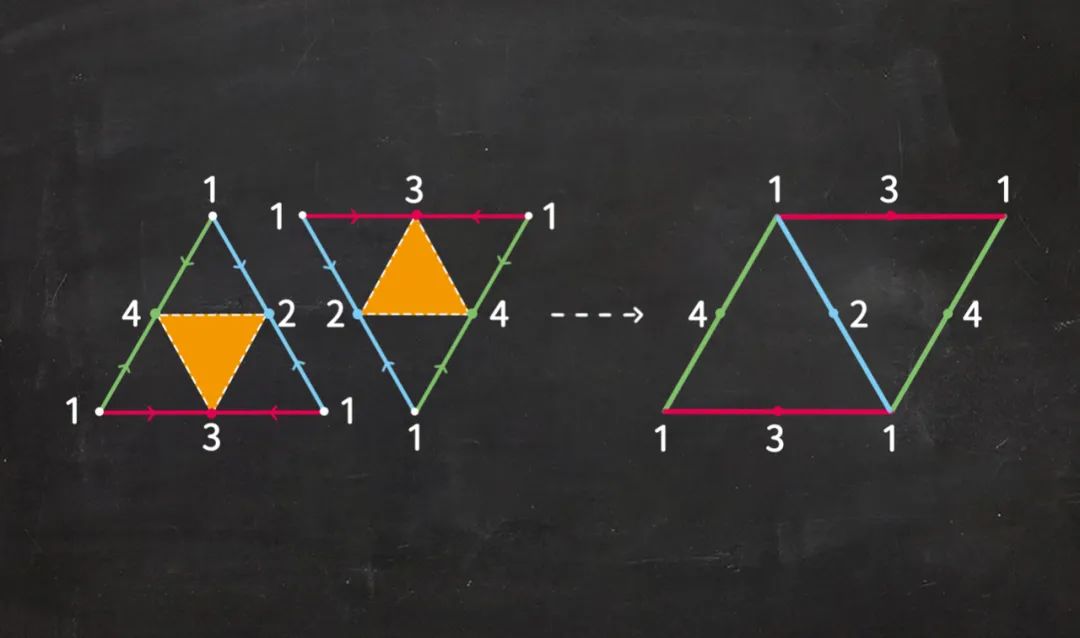
жң¬ж–ҮеӣҫзүҮ
еҰӮдёҠеӣҫе·Ұиҫ№жүҖзӨә пјҢ еҪ“жҲ‘们жғіиҰҒе°ҶжӯЈдёүи§’еҪўжҒўеӨҚжҲҗжӯЈеӣӣйқўдҪ“ж—¶ пјҢ еҸӘйңҖе°ҶйўңиүІзӣёеҗҢзҡ„иҫ№еҜ№зқҖзІҳеҗҲеҚіеҸҜпјӣиҖҢиҰҒе°ҶдёӨдёӘеұ•ејҖеӣҫеҪўз»“еҗҲ пјҢ еҲҷеҸӘйңҖе°Ҷе…¶дёӯдёҖдёӘж—ӢиҪ¬180В° пјҢ еҶҚе°Ҷе®ғ们жӢјеңЁдёҖиө·еҚіеҸҜпјҲеҰӮдёҠеӣҫеҸіжүҖзӨәпјү гҖӮ еҰӮжһң继з»ӯеҗ‘еҗ„дёӘж–№еҗ‘ж— йҷҗең°иҝӣиЎҢиҝҷз§Қз»“еҗҲ пјҢ е°ұиғҪе°ҶиҝҷдәӣеӣҫеҪўеҜҶй“әеҲ°ж•ҙдёӘз©әй—ҙ гҖӮ
зҺ°еңЁ пјҢ еңЁжӯЈеӣӣйқўдҪ“дёҠзҡ„зӣҙзәҝй—®йўҳиў«жј”еҸҳжҲҗдәҶ пјҢ жҲ‘们жҳҜеҗҰеҸҜд»ҘеңЁеұ•ејҖеӣҫдёҠз”»еҮәдёҖжқЎзӣҙзәҝ пјҢ зӣҙзәҝжүҖиҝһжҺҘзҡ„дёӨзӮ№е…·жңүзӣёеҗҢзҡ„йўңиүІпјҹ
е…¶е®һ пјҢ еҜ№з”ұдёүи§’еҪўжһ„жҲҗзҡ„жӯЈеӣӣйқўдҪ“гҖҒе…«йқўдҪ“гҖҒдәҢеҚҒйқўдҪ“ пјҢ д»ҘеҸҠз”ұжӯЈж–№еҪўжһ„жҲҗзҡ„з«Ӣж–№дҪ“ пјҢ ж•°еӯҰ家们早已зҹҘйҒ“иҝҷдёӘй—®йўҳзҡ„зӯ”жЎҲпјҡеҜ№дәҺиҝҷеӣӣз§ҚжӯЈеӨҡйқўдҪ“жқҘиҜҙ пјҢ д»Һд»»дҪ•дёҖдёӘйЎ¶зӮ№ејҖе§ӢжІҝзӣҙзәҝеүҚиҝӣ пјҢ йғҪеҝ…е®ҡиҰҒз»ҸиҝҮеҸҰдёҖдёӘйЎ¶зӮ№жүҚиғҪйҮҚиҝ”еҺҹзӮ№ гҖӮ иҝҷж„Ҹе‘ізқҖ пјҢ вҖңжӯЈеӣӣйқўдҪ“жҳҹзҗғвҖқдёҠж•°еӯҰ家жҳҜж— жі•йҳ»жӯўз§ҚжӨҚеңЁе…¶д»–йЎ¶зӮ№дёҠзҡ„зҺ«з‘°иў«зҫҠеҗғжҺүзҡ„еҺ„иҝҗзҡ„ гҖӮ
йӮЈд№Ҳ пјҢ 第дәҢдёӘж•…дәӢдёӯзҡ„вҖңзӨҫжҒҗвҖқж•°еӯҰ家 пјҢ жҳҜдёҚжҳҜд№ҹеҗҢж ·ж— жі•еҰӮж„ҝиҝӣиЎҢжғіиҰҒзҡ„ж•ЈжӯҘдәҶпјҹ
е…¶е®һдёҖзӣҙд»ҘжқҘ пјҢ 并没жңүдәәзҹҘйҒ“з”ұ12дёӘдә”иҫ№еҪўз»„жҲҗзҡ„жӯЈеҚҒдәҢйқўдҪ“еңЁиҝҷдёӘй—®йўҳдёӯзҡ„жғ…еҶө гҖӮ дёҺе…¶д»–еӣӣз§ҚжӯЈеӨҡйқўдҪ“зӣёжҜ” пјҢ жӯЈеҚҒдәҢйқўдҪ“жңүдёҖдёӘжҳҫиҖҢжҳ“и§Ғзҡ„дёҚеҗҢпјҡеҜ№дәҺжӯЈеӣӣйқўдҪ“гҖҒз«Ӣж–№дҪ“гҖҒе…«йқўдҪ“е’ҢдәҢеҚҒйқўдҪ“ пјҢ жһ„жҲҗдәҶе®ғ们зҡ„еӣҫеҪўпјҲдёүи§’еҪўе’ҢжӯЈж–№еҪўпјүеҸҜд»ҘеҜҶй“әж•ҙдёӘз©әй—ҙпјӣиҖҢжӯЈеҚҒдәҢйқўдҪ“зҡ„еұ•ејҖеӣҫеҪўпјҲжӯЈдә”иҫ№еҪўпјүеҚҙдёҚиғҪеҒҡеҲ°иҝҷдёҖзӮ№ гҖӮ
жҺЁиҚҗйҳ…иҜ»
- еҘҘж–ҜеҚЎ|з”ҹиҖҢиҮӘз”ұпјҢеҚҒдәҢе№ҙеҪ’жқҘд»Қ然еҝғжҖҖж„ҹжҒ©
- еҲҳжҷ“еәҶ |еҲҳжҷ“еәҶеҸӘжҙ»еңЁзІҫдҝ®еӣҫдёӯпјҢз”ҹеӣҫз®ҖзӣҙеҲӨиӢҘдёӨдәәпјҢзІүеә•жҺ©йҘ°дёҚдәҶе®№йўң
- йЈҺйҷ©|гҖҠеӨ©еӨ©еҗ‘дёҠгҖӢеҶ еҗҚе•ҶжІЎдәҶпјҢеҚҒдәҢе№ҙзҡ„йҮ‘зүҢиҠӮзӣ®пјҢеҰӮд»ҠиҰҒйқўдёҙеҒңж’ӯйЈҺйҷ©еҗ—пјҹ
- жҳҺжҳҹе…«еҚҰ|жӣҫжҙ»еңЁе·©дҝҗеҪұеӯҗдёӢзҡ„з« еӯҗжҖЎиҜ„гҖҠеӨәеҶ гҖӢпјҢеҰӮд»ҠдәҢдәәе·ІжіҫжёӯеҲҶжҳҺпјҒ
- жғ…з»ӘеҢ–|дёүдёӘз”ҹиӮ–жҳҹеә§жҳҜе№ійқҷзҡ„пјҢдёҚжҳҜжғ…з»ӘеҢ–е’Ңи¶іжҷәеӨҡи°Ӣ
- йІңй—»иҜҙ|NASAзҡ„科еӯҰ家称дәәзұ»з”ҹжҙ»еңЁеӨ–жҳҹз”ҹзү©жүҖи®ҫи®Ўзҡ„е…ЁжҒҜеӣҫдёӯ
- йҖ еһӢ|дёҚиүҜдәә第еӣӣеӯЈпјҡеҚҒдәҢеі’дә”еӨ§ејәиҖ…иҝҪжқҖжқҺжҳҹдә‘пјҢж–°еҘізҘһжқҘж•‘еңәпјҢдёҚиүҜеё…д»ҚжңүжҲҸд»ҪпјҒ
- еӣҪж°‘и®°иҖ…|жҲҗжҜ…жңҖж–°йҮҮи®ҝжҡҙйңІйўңеҖјзјәзӮ№пјҢи„ёж–№иӨ¶еӯҗеӨҡпјҢиў«еҗҗж§ҪеҸӘиғҪжҙ»еңЁеҸӨиЈ…йҮҢ
- жөҰжҳҘ马|иҙөеңҲеҚҒдәҢдј иҜҙпјҡгҖҠиЎҖиүІжҳҹжңҹдёҖгҖӢйқһжӯЈеёёжӯ»дәЎдәӢ件
- еёёй©»|жҒӯе–ңJustinй»„жҳҺжҳҠжҲҗдёәгҖҠеҝ«д№җеӨ§жң¬иҗҘгҖӢеҚҒдәҢжңҹеёёй©»еҳүе®ҫ









![[дәәж°‘еүҚзәҝ]дҫҰеҜҹе…өйҮҢеҪ“е°–е…өпјҒпјҢ00еҗҺдёҠзӯүе…ө](https://imgcdn.toutiaoyule.com/20200502/20200502161114462652a_t.jpeg)






