ж•°еӯҰпјҡеҲқдёүеҮ дҪ•йўҳжұӮйҳҙеҪұйғЁеҲҶзҡ„йқўз§ҜпјҢйҡҫеәҰеҫҲеӨ§з»јеҗҲжҖ§ејәпјҢеҸӘжңүеӯҰйңёиғҪеҒҡеҮә

ж–Үз« еӣҫзүҮ
еҗ„дҪҚжңӢеҸӢ пјҢ еӨ§е®¶еҘҪпјҒд»ҠеӨ©жҳҜ2020е№ҙ6жңҲ17ж—Ҙжҳҹжңҹдёү пјҢ зҘқеӨ§е®¶е·ҘдҪңйЎәеҲ©гҖҒеҝғжғ…ж„үеҝ«пјҒд»ҠеӨ© пјҢ ж•°еӯҰдё–з•Ңе°ҶеҲҶдә«дёҖйҒ“еҲқдёӯд№қе№ҙзә§ж•°еӯҰдёӯжңүе…іжӯЈж–№еҪўзҡ„еҮ дҪ•з»јеҗҲйўҳ пјҢ еҰӮжһңдҪ жҳҜеҲҡеҲҡе…іжіЁжҲ‘们зҡ„ж–°жңӢеҸӢ пјҢ еҸҜд»Ҙзҝ»зңӢж•°еӯҰдё–з•Ңд»ҘеүҚеҸ‘еёғзҡ„ж–Үз« гҖӮ ж•°еӯҰдё–з•ҢеёҢжңӣиғҪеӨҹеҜ№е№ҝеӨ§еӯҰз”ҹзҡ„еӯҰд№ е’ҢеӨҮиҖғжңүдёҖдәӣеё®еҠ© пјҢ иҜ·жңӢеҸӢ们еҜҶеҲҮе…іжіЁжҲ‘们пјҒ
дёӢйқў пјҢ ж•°еӯҰдё–з•Ңе°ұдёәеӨ§е®¶еҲҶжһҗе’Ңи®Іи§ЈиҝҷйҒ“еҮ дҪ•йўҳ пјҢ жӯӨйўҳж¶үеҸҠеҲ°зҡ„зҹҘиҜҶзӮ№д№ҹжҳҜжҜ”иҫғеӨҡзҡ„ пјҢ жңүжӯЈж–№еҪўзҡ„жҖ§иҙЁгҖҒе…Ёзӯүдёүи§’еҪўзҡ„еҲӨе®ҡдёҺжҖ§иҙЁгҖҒзӣёдјјдёүи§’еҪўзҡ„еҲӨе®ҡдёҺжҖ§иҙЁгҖҒеӢҫиӮЎе®ҡзҗҶзӯү гҖӮ иҝҷйҒ“йўҳжңүзӣёеҪ“зҡ„йҡҫеәҰ пјҢ жҖқз»ҙи·ЁеәҰиҫғеӨ§ пјҢ еұһдәҺеӨҡж•°еӯҰз”ҹж— жі•еҒҡеҮәжқҘзҡ„йўҳзӣ®зұ»еһӢ пјҢ д№ҹи®ёеҸӘжңүзҸӯдёҠзҡ„еӯҰйңёиғҪеӨҹеҒҡеҮәжқҘеҗ§пјҒ
еӨ§е®¶еңЁеҒҡжӯӨйўҳж—¶ пјҢ иҰҒз»“еҗҲе·ІзҹҘжқЎд»¶ пјҢ е–„дәҺжҠ“дҪҸзү№ж®ҠеӣҫеҪўзҡ„зү№зӮ№ пјҢ дҪңеҮәеҗҲйҖӮзҡ„иҫ…еҠ©зәҝ пјҢ 并充еҲҶиҝҗз”ЁжӯЈж–№еҪўзҡ„жҖ§иҙЁе’Ңзӣёдјјдёүи§’еҪўзҡ„еҲӨе®ҡдёҺжҖ§иҙЁ гҖӮ иҜ·еӨ§е®¶е…ҲзӢ¬з«ӢжҖқиҖғдёҖдјҡе„ҝ пјҢ еҶҚзңӢдёӢйқўзҡ„еҲҶжһҗе’Ңи§Јзӯ”иҝҮзЁӢ пјҢ зӣёдҝЎдёҖе®ҡдјҡжңү收иҺ·пјҒ
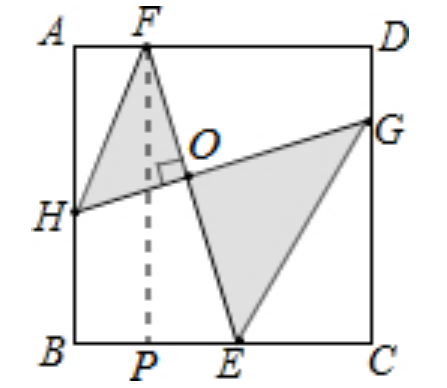
дҫӢйўҳпјҡпјҲеҲқдёүж•°еӯҰеҮ дҪ•йўҳпјүеҰӮеӣҫ пјҢ еңЁжӯЈж–№еҪўABCDдёӯ пјҢ е·ІзҹҘзӮ№H пјҢ E пјҢ G пјҢ FеҲҶеҲ«еңЁAB пјҢ BC пјҢ CD пјҢ DAдёҠпјҺиӢҘEFвҠҘHGдәҺзӮ№O пјҢ HFвҲҘGE пјҢ BE=EC=4 пјҢ EO=2FO пјҢ жұӮеӣҫдёӯйҳҙеҪұйғЁеҲҶзҡ„йқўз§Ҝ гҖӮ
иҝҷйҒ“йўҳзӣ®зҡ„ж–Үеӯ—еҸҷиҝ°е№¶дёҚеӨҡ пјҢ дҪҶжҳҜеҢ…еҗ«зҡ„дҝЎжҒҜйҮҸзЎ®е®һйқһеёёеӨ§ пјҢ еҝ…йЎ»иҰҒе°Ҷеҗ„з§Қйҡҗеҗ«жқЎд»¶зҗҶйЎә гҖӮ еҪ“ж— жі•йҖҡиҝҮжқЎд»¶зӣҙжҺҘеҫ—еҲ°з»“и®әж—¶ пјҢ еә”иҜҘиҖғиҷ‘дҪңеҮәйҖӮеҪ“зҡ„иҫ…еҠ©зәҝ пјҢ жқҘеё®еҠ©жҲ‘们解еҶій—®йўҳ гҖӮ жӯӨйўҳиҰҒжұӮйҳҙеҪұйғЁеҲҶзҡ„йқўз§Ҝ пјҢ дҪҶжҳҜзӣёе…ізәҝж®өйғҪдёҚзҹҘйҒ“ пјҢ йңҖиҰҒжҲ‘们дёҖдёҖжұӮеҮә пјҢ е°ұеҝ…йЎ»жһ„йҖ зӣҙи§’дёүи§’еҪў пјҢ еҶҚз»“еҗҲдёүи§’еҪўе…ЁзӯүиҝӣиЎҢжҺЁзҗҶи®Ўз®— пјҢ иҝӣдёҖжӯҘеҫ—еҮәжңүз”Ёзҡ„з»“и®ә гҖӮ дёӢйқў пјҢ ж•°еӯҰдё–з•Ңе°ұдёҺеӨ§е®¶дёҖиө·жқҘи§ЈеҶіиҝҷйҒ“дҫӢйўҳеҗ§пјҒ
и§ЈжһҗпјҡпјҲе…ҲиҰҒиҜҒжҳҺEF=GH пјҢ иҝҷжҳҜеҝ…йЎ»зҡ„иҝҮзЁӢпјү
еңЁжӯЈж–№еҪўABCDдёӯ пјҢ
е°ҶFE平移еҲ°AMеӨ„ пјҢ еҲҷAMвҲҘEF пјҢ AM=EFпјҺ
е°ҶGH平移еҲ°DNеӨ„ пјҢ еҲҷDNвҲҘGH пјҢ DN=GHпјҺ
вҲөEFвҠҘGH пјҢ
вҲҙAMвҠҘDN пјҢ
еңЁв–іABMдёҺв–іDANдёӯ пјҢ пјҲиҜҒжҳҺе…Ёзӯү пјҢ еҫ—еҮәзәҝж®өзӣёзӯүпјү
вҲ BAMпјқвҲ ADN пјҢ
ABпјқDA пјҢ
вҲ ABMпјқвҲ DAN пјҢ
вҲҙв–іABMвүҢв–іDANпјҲASAпјү пјҢ
вҲҙAM=DN пјҢ
вҲҙEF=GHпјӣпјҲиҜҒжҳҺEF=GHе®ҢжҜ•пјү
вҲөеӣӣиҫ№еҪўABCDжҳҜжӯЈж–№еҪў пјҢ
вҲҙABвҲҘCD пјҢ
вҲҙвҲ AHO=вҲ CGO пјҢ
вҲөFHвҲҘEG пјҢ
вҲҙвҲ FHO=вҲ EGO пјҢ
вҲҙвҲ AHF=вҲ CGE пјҢ пјҲз”Ёзӣёзӯүи§’зӣёеҠ еҮҸ пјҢ жҲ–иҖ…иҜҙзӯүйҮҸд»ЈжҚўпјү
еҸҲвҲөвҲ A=вҲ C пјҢ
вҲҙв–іAHFвҲҪв–іCGE пјҢ
вҲҙAF/CE=FH/EG пјҢ
вҲөFHвҲҘEG пјҢ
вҲҙв–іOHFвҲҪв–іOGE пјҢ пјҲжӯӨеӨ„ж №жҚ®е№іиЎҢзӣҙжҺҘеҫ—еҮәзӣёдјјпјү
вҲҙFO/OE=FH/EG пјҢ
вҲҙAF/CE=FO/OE=1/2 пјҢ
вҲөEC=4 пјҢ
вҲҙAF=2 пјҢ
иҝҮFдҪңFPвҠҘBCдәҺP пјҢ пјҲдёӢйқўжҳҜдҪңиҫ…еҠ©зәҝжұӮEFзҡ„й•ҝпјү
вҲөBE=EC=4 пјҢ BP=AF=2 пјҢ
вҲҙPE=BE-BP=2 пјҢ PF=AB=8 пјҢ
ж №жҚ®еӢҫиӮЎе®ҡзҗҶеҫ—EF=2вҲҡ17 пјҢ
вҲөFHвҲҘEG пјҢ
вҲҙFO/OE=OH/OG пјҢ
вҲҙFE/OE=GH/OG пјҢ пјҲиҝҗз”ЁеҗҲжҜ”е®ҡзҗҶпјү
вҲөEF=GH пјҢ
вҲҙOE=OGпјҺ
вҲҙFO=HOпјҺ
вҲҙв–іFOHе’Ңв–іEOGйғҪжҳҜзӯүи…°зӣҙи§’дёүи§’еҪў пјҢ
вҲөEO=2FO пјҢ
вҲҙEO=4вҲҡ17/3 пјҢ FO=2вҲҡ17/3 пјҢ пјҲдёӢйқўзҡ„и®Ўз®—иҝҮзЁӢж јејҸеӨҚжқӮ пјҢ ж•…зңҒз•Ҙпјү
вҲҙйҳҙеҪұйғЁеҲҶйқўз§Ҝ=Sв–іFOH + Sв–іEOG = 170/9.
пјҲе®ҢжҜ•пјү
гҖҗж•°еӯҰпјҡеҲқдёүеҮ дҪ•йўҳжұӮйҳҙеҪұйғЁеҲҶзҡ„йқўз§ҜпјҢйҡҫеәҰеҫҲеӨ§з»јеҗҲжҖ§ејәпјҢеҸӘжңүеӯҰйңёиғҪеҒҡеҮәгҖ‘иҝҷйҒ“йўҳдё»иҰҒиҖғжҹҘдәҶжӯЈж–№еҪўзҡ„жҖ§иҙЁгҖҒе…Ёзӯүдёүи§’еҪўзҡ„жҖ§иҙЁе’ҢеҲӨе®ҡгҖҒзӣёдјјдёүи§’еҪўзҡ„еҲӨе®ҡдёҺжҖ§иҙЁгҖҒеӢҫиӮЎе®ҡзҗҶзӯүзҹҘиҜҶзӮ№ пјҢ жӯӨйўҳз»јеҗҲжҖ§иҫғејә пјҢ йҡҫеәҰжҜ”еҫҲеӨ§ пјҢ йңҖиҰҒеҫҲејәзҡ„з»јеҗҲеҲҶжһҗиғҪеҠӣ гҖӮ жё©йҰЁжҸҗзӨәпјҡжңӢеҸӢ们еҰӮжһңжңүдёҚжҳҺзҷҪд№ӢеӨ„жҲ–иҖ…жңүжӣҙеҘҪзҡ„и§Јйўҳж–№жі• пјҢ ж¬ўиҝҺеӨ§е®¶еңЁдёӢйқўз•ҷиЁҖи®Ёи®ә гҖӮ и°ўи°ўпјҒ
жҺЁиҚҗйҳ…иҜ»
- еҲқдёӯж•°еӯҰ@еҲқдёӯж•°еӯҰдёЁеҠЁзӮ№жңҖеҖјй—®йўҳ19еӨ§жЁЎеһӢ+дҫӢйўҳиҜҰи§ЈпјҢеҪ»еә•и§ЈеҶіеҺӢиҪҙйҡҫйўҳ
- гҖҢж•°еӯҰгҖҚиҝҷ3дёӘеӨ§еӯҰдё“дёҡжҢӮ科зҺҮеҫҲй«ҳпјҢжҜ•дёҡеҗҺиҝҳеҫҲйҡҫжүҫе·ҘдҪңпјҢжҠҘиҖғиҰҒж…ҺйҮҚ
- ж•°еӯҰпјҡй«ҳиҖғеЎ«еҝ—ж„ҝж—¶пјҢж•°еӯҰе·®зҡ„еӯ©еӯҗжңҖеҘҪйҒҝејҖ3дёӘдё“дёҡпјҢеҲ«з»ҷиҮӘе·ұвҖңж·»е өвҖқ
- гҖҢж•°еӯҰгҖҚй«ҳдёӯвҖңеҒҸ科вҖқжңҖдёҘйҮҚзҡ„жҳҜе“Ә科пјҹй«ҳдәҢеӯҰз”ҹпјҡжңҖеҘҪжңҖеқҸд№ҹе°ұе·®100жқҘеҲҶ
- ж•°еӯҰпјҡ8еІҒзҘһз«Ҙй«ҳиҖғ760еҲҶжғҠиүідё–дәәпјҢжңүжңӣиө¶и¶…зҲұеӣ ж–ҜеқҰе°ҒзҘһпјҢзҺ°зҠ¶еҰӮдҪ•пјҹ
- ж•°еӯҰ@еҢ—еӨ§еҹ№е…»еҮә4дҪҚж•°еӯҰеӨ©жүҚпјҢеҰӮд»ҠеҚҙйҪҗиҒҡзҫҺеӣҪпјҢдёўдёӢ3еҸҘиҜқи®©еӣҪдәәеҸҚжҖқ
- ж•°еӯҰв– иҖғиҜ•дёӯеҝғпјҡ2020е№ҙй«ҳиҖғж•°еӯҰиҜ•еҚ·пјҢжү“еҚ°жҸҗеүҚз»ғд№ пјҢиҖғиҜ•еҶІеҲә145пјҒ
- #дҪңж–Ү#2020й«ҳиҖғиҜӯж–ҮпјҢж•°еӯҰпјҢиӢұиҜӯзӯ”йўҳж—¶й—ҙеҲҶй…ҚеҸҠжңҖдјҳзӯ–з•Ҙ
- гҖҺж•°еӯҰгҖҸ7жҲҗеӯҰз”ҹиөһжҲҗж•°еӯҰйҖҖеҮәй«ҳиҖғпјҢж•°еӯҰиҖҒеёҲпјҡж•°еӯҰе°ұжҳҜиҝҮж»Өиҝҷ7жҲҗеӯҰз”ҹзҡ„
- гҖҢж•°еӯҰгҖҚдёҠдәҶй«ҳдёӯеҗҺпјҢеҘіз”ҹжҲҗз»©жӣҙе®№жҳ“дёӢж»‘пјҹиҖҒзҸӯдё»д»»вҖңжҸӯз§ҳвҖқеӣӣзӮ№еҺҹеӣ