гҖҗеҸӨе·ҙжҜ”дјҰгҖ‘дәә们жҳҜжҖҺд№ҲеҸ‘зҺ°ПҖзҡ„е‘ўпјҹ
ж–Үз« еӣҫзүҮ

ж–Үз« еӣҫзүҮ
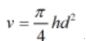
ж–Үз« еӣҫзүҮ
ж–Үз« еӣҫзүҮ

ж–Үз« еӣҫзүҮ

ж–Үз« еӣҫзүҮ
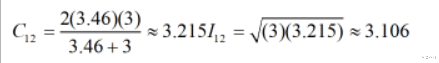
ж–Үз« еӣҫзүҮ
ж–Үз« еӣҫзүҮ
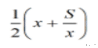
ж–Үз« еӣҫзүҮ
дәә们жҳҜжҖҺд№ҲеҸ‘зҺ°ПҖзҡ„е‘ўпјҹжҲ‘们еҸҲжҳҜжҖҺд№ҲзҹҘйҒ“ПҖиҝ‘дјјдәҺ3.14...зҡ„е‘ўпјҹгҖҠзү©зҗҶеӯҰ家гҖӢжқӮеҝ—ж—©еңЁ2018е№ҙ8жңҲ24ж—ҘеҸ‘ж–Үз§°пјҡеҫҲйҒ—жҶҫ пјҢ ПҖзҡ„дҪҝз”Ёж—¶й—ҙжҜ”еҺҶеҸІдёҠзҡ„и®°иҪҪж—¶й—ҙиҝҳиҰҒж—© пјҢ жүҖд»Ҙ пјҢ иҝҷдёӘй—®йўҳжІЎдәәиғҪи§Јзӯ” гҖӮ дҪҶжҳҜжҚ®еҺҶеҸІи®°иҪҪ пјҢ ПҖеңЁжңҖејҖе§ӢдҪҝз”Ёж—¶иҝҳдёҚз®—еӨӘеӨҚжқӮ пјҢ еӣ жӯӨжҲ‘们еҸҜд»ҘиҝӣиЎҢеӨ§иғҶзҢңжөӢ гҖӮ
дј—жүҖе‘ЁзҹҘ пјҢ ПҖжҳҜеңҶзҡ„е‘Ёй•ҝдёҺзӣҙеҫ„д№ӢжҜ” гҖӮ дёҖеҲҮдёҺеңҶзӣёе…ізҡ„еҶ…е®№йғҪиғҪе’ҢПҖжүҜдёҠе…ізі» гҖӮ
жөӢйҮҸд»»ж„ҸдёҖдёӘеңҶзҡ„е‘Ёй•ҝдёҺзӣҙеҫ„ пјҢ 然еҗҺе°ҶдёӨж•°зӣёйҷӨ пјҢ дҪ е°ұеҸҜд»Ҙеҫ—еҲ°ПҖдәҶ гҖӮ
д»»ж„ҸдёҖдёӘеӣәе®ҡеҪўзҠ¶зҡ„зӣҙеҫ„йғҪдёҺе…¶е‘Ёй•ҝжҲҗжӯЈжҜ” пјҢ дҪҶиҝҷжІЎд»Җд№Ҳзү№еҲ«зҡ„ гҖӮ жӯӨе®ҡи®әйҖӮз”ЁдәҺд»»ж„ҸеҪўзҠ¶ гҖӮ еҰӮжһңе°Ҷд»»ж„ҸеӣҫеҪўжү©еӨ§дёҖеҖҚ пјҢ еҲҷе…¶зӣҙеҫ„дёҺе‘Ёй•ҝйғҪе°Ҷжү©еӨ§дёҖеҖҚ пјҢ е®ғ们д№Ӣй—ҙзҡ„жҜ”зҺҮд»ҚдҝқжҢҒдёҚеҸҳ гҖӮ
е°ҶдёҖдёӘжӯЈж–№еҪўзҡ„е‘Ёй•ҝйҷӨд»Ҙе…¶иҫ№й•ҝж°ёиҝңзӯүдәҺ4 гҖӮ
еңҶзҡ„е‘Ёй•ҝдёҺе…¶зӣҙеҫ„зҡ„жҜ”дҫӢжҳҜдёҖдёӘе®ҡеҖј пјҢ иҖҢдәә们и®ӨиҜҶеҲ°иҝҷдёҖзӮ№еҚҙж—©дәҺеҺҶеҸІи®°иҪҪ гҖӮ дҪҶиҜҘдёҚе®Ңе…ЁзӯүдәҺдёүзҡ„ж•°еҖјиҝҳйңҖдёҚж–ӯзІҫзЎ® гҖӮ иҰҒи®Ўз®—еҮәиҝҷдёӘе…·жңүж— йҷҗдёҚеҫӘзҺҜзү№зӮ№пјҲд»Ҙ3.14159265358979323846264...ејҖеӨҙпјүзҡ„ж•°еҖјиҝҳйңҖиҰҒдёҖзӮ№ж•°еӯҰе’Ңж—¶й—ҙ гҖӮ
зәҰ4000е№ҙеүҚ пјҢ еҸӨе·ҙжҜ”дјҰзҹізў‘дёҠи®°иҪҪПҖ=3 гҖӮ еҸҜиҝҷдёӘж•°еҖјзңӢиө·жқҘдјјд№ҺдёҚжҳҜйӮЈд№ҲеҮҶзЎ® гҖӮ
еҰӮжһңдҪ е°ҶдёҖж №з»іеӯҗдёҖз«Ҝеӣәе®ҡдҪҸ пјҢ еҸҰдёҖз«Ҝз»‘дёҠй№…жҜӣ笔жҲ–жңЁзӮӯ пјҢ йӮЈд№ҲдҪ е°ұеҸҜд»Ҙз”»еҮәдёҖдёӘиҝ‘д№Һе®ҢзҫҺзҡ„еңҶ гҖӮ еҰӮжһңз”ЁдёҖж №жӣҙй•ҝзҡ„з»іеӯҗпјҲиҮіе°‘еҫ—жҳҜд№ӢеүҚйӮЈж №з»іеӯҗзҡ„2ПҖеҖҚпјүе’ҢдёҖжҠҠе°әеӯҗ пјҢ дҪ е°ұеҸҜд»ҘжөӢйҮҸеҮәжүҖз”»зҡ„еңҶзҡ„е‘Ёй•ҝ гҖӮ еҸӘиҰҒдҪ д»”з»Ҷдәӣ пјҢ дҪ е°ұеҸҜд»ҘеҸ‘зҺ° пјҢ еҫҲжҳҫ然ПҖвү 3 гҖӮ еҸӘиҰҒжөӢйҮҸиҜҜе·®дҪҺдәҺ4% пјҢ дҪ е°ұеҸҜд»ҘзңӢеҮәе…¶дёӯзҡ„е·®и·қ гҖӮ еҸӨе·ҙжҜ”дјҰдәәзј–еҶҷдәҶгҖҠжұүи°ҹжӢүжҜ”жі•е…ёгҖӢ пјҢ е»әйҖ дәҶи®ёеӨҡд»ӨдәәжғҠеҸ№зҡ„е»әзӯ‘ пјҢ з”ұжӯӨеҸҜи§Ғ пјҢ 他们жңүеҸҜиғҪеҫҲж—©е°ұжңүдәҶд»ҘеҺҳзұідёәжөӢйҮҸеҲ»еәҰзҡ„зұіе°ә гҖӮ дәӢе®һиҜҒжҳҺ пјҢ дёҠиҝ°зҡ„зҹізў‘еҫҲеҸҜиғҪе°ұжҳҜдёҖдёӘи®°еҪ•дәҶеңҶиҝ‘дјјеҖјеӨ§иҮҙеҢәй—ҙзҡ„вҖңеӨҮеҝҳеҪ•вҖқ гҖӮ жҲ‘们зҹҘйҒ“ пјҢ еҸӨе·ҙжҜ”дјҰдәәе·Із»Ҹеҫ—еҮә25/8=3.125 пјҢ иҖҢиҝҷдёӘиҝ‘дјјеҖјзҡ„иҜҜе·®еңЁ0.5%д»ҘеҶ… гҖӮ еҫ—еҮәиҝҷдёӘеҖјеҜ№дәҺйқ’й“ңж—¶д»Јзҡ„дәә们жқҘиҜҙ пјҢ е·Із»ҸеҫҲдәҶдёҚиө·дәҶ гҖӮ
еҸӘиҰҒдҪ еңЁеҒҡж¶үеҸҠеңҶзҡ„ж•°еӯҰеҶ…е®№ пјҢ ПҖе°ұдјҡж— ж—¶ж— еҲ»дёҚеҮәзҺ°еңЁдҪ зңјеүҚ пјҢ еӣ жӯӨеҸӨд»Јеҫ—дәә们жңүеҚғеҚғдёҮдёҮж¬ЎжңәдјҡеҸ‘зҺ°ПҖзҡ„еӯҳеңЁ пјҢ жүҖд»ҘжҲ‘д»¬ж— жі•зЎ®е®ҡ究з«ҹжҳҜе“ӘдёҖж¬ЎеҒ¶з„¶жңәдјҡдҪҝеҫ—дәә们зңҹжӯЈеҸ‘зҺ°дәҶПҖпјҲиҝҷдёҖзӮ№жӯЈжҳҜжҜ”еҺҶеҸІи®°еҪ•иҝҳж—©зҡ„з ”з©¶еҸ‘зҺ°зҡ„зјәзӮ№пјү гҖӮ дҫӢеҰӮ пјҢ жңүдёҖдёӘй«ҳдёәh пјҢ зӣҙеҫ„дёәdзҡ„жЎ¶зҡ„ пјҢ е®№йҮҸдёә
жҺЁиҚҗйҳ…иҜ»
- иғ–еӯҗ|жҖҺж ·еӨҡејҖдјҳй…·гҖҒ200дёӘиұҶз“ЈжҖҺд№Ҳжү№йҮҸеҸ‘е°Ҹи§Ҷйў‘пјҹ
- еҲқжңЁеҪұи§Ҷ|жҖҺд№ҲжүҚиғҪеҒҡеҘҪж·ҳе®қзӣҙж’ӯпјҹ
- е°Ҹзүӣзүӣ讲解科жҠҖ|зҪ‘еҸӢпјҡдё»еҠЁйҷҚеҷӘж–№еҗ‘еҜ№дәҶпјҢзңҹж— зәҝиҖіжңәжҖҺд№ҲйҖүпјҹзғӯй—ЁиҖҒж¬ҫVSжҳҺжҳҹж–°ж¬ҫ
- гҖҺеӨ–жҳҹдәәгҖҸеӨ–жҳҹдәәеқ иҗҪд№Ӣең°пјҢеҸ‘зҺ°зҘһз§ҳйҮ‘еұһзўҺзүҮпјҢдёҠйқўиҝҳжңүдёӯж–Үеӯ—ж ·пјҢжҖҺд№ҲеӣһдәӢ
- е–ңеҲ©з§‘жҠҖ|иҝҳи®©е°ҸзұіжҖҺд№ҲзҺ©пјҹпјҢvivoз»ҲдәҺж”ҫеӨ§жӢӣпјҒ6+256+22.5WеҸӘиҰҒ1488
- е°Ҹејәе№Ҫй»ҳ|е…¬еҸёеҰӮдҪ•еҒҡеҘҪзҪ‘з»ңиҗҘй”ҖжҺЁе№ҝжүҫе®ўжҲ·пјҢеӣӯжһ—иҠұеҚүиЎҢдёҡдјҒдёҡжҖҺд№ҲеҲ©з”ЁзҪ‘з»ңжҺЁе№ҝеј•жөҒиҺ·е®ў
- йЈҺйӣЁеҗҢиҝӣжӯҘ|е…¬еҸёеҰӮдҪ•еҒҡеҘҪзҪ‘з»ңиҗҘй”ҖжҺЁе№ҝжүҫе®ўжҲ·пјҢж—…жёёиЎҢдёҡдјҒдёҡжҖҺд№ҲеҲ©з”ЁзҪ‘з»ңжҺЁе№ҝеј•жөҒиҺ·е®ў
- гҖҺйҒ—йӘёгҖҸеӨ§иҲӘжө·е®¶е“ҘдјҰеёғжҳҜжҖҺд№Ҳжӯ»зҡ„пјҹд»–зҡ„жӯ»дәЎеҸҲдёәдәәзұ»еёҰжқҘдәҶжҖҺж ·зҡ„и°ңйўҳпјҹ
- гҖҗзҘһиҲҹгҖ‘зҘһиҲҹ笔记жң¬жҖҺд№Ҳж ·пјҢзҠ№иұ«иҜҘдёҚиҜҘдёҠиҲ№пјҢжқҘзңӢжҲҳзҘһZ7ct5n1дёҠжүӢдҪ“йӘҢ
- еӨ§еӨҙе“Ҙе“ҘиҜҙеЁұд№җ|дёҖе№ҙдёҚз”ЁиҝҳиҠұе‘—зҡ„ж”Ҝд»ҳе®қз”ЁжҲ·пјҢеҰӮд»ҠжҖҺд№Ҳж ·дәҶпјҹпјҢжҠҪдёӯвҖңиҠұиҠұеҚЎвҖқ