江苏龙网

  1. 首页 > 人文 > >

密码学@宇宙密码——素数的自然之美，无数天才为其折腰


密码学@宇宙密码——素数的自然之美，无数天才为其折腰
文章图片
密码学@宇宙密码——素数的自然之美，无数天才为其折腰
文章图片
密码学@宇宙密码——素数的自然之美，无数天才为其折腰
文章图片
密码学@宇宙密码——素数的自然之美，无数天才为其折腰
文章图片
密码学@宇宙密码——素数的自然之美，无数天才为其折腰

什么是质数？
质数的定义很简单 。
定义：质数是一个只能被1和它本身整除的整数 。
换句话说 ， 质数是一个自然数p >1 ， 它不能表示为两个较小自然数的乘积 。 因此 ， 一个质数有两个正的因数 。 前25个质数：
2、3、5、7、11、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89……
我们还有一个美丽的质数 ， 贝尔芬格质数
1000000000000066600000000000001 = 10^30+ 666 + 10^14+ 1
这是1 ， 后面是13个0 ， 然后是666 ， 再后面是13个0 ， 最后是1 。 对于大多数数学家来说 ， 这个质数不可能是一个巧合 。 这是一种艺术！
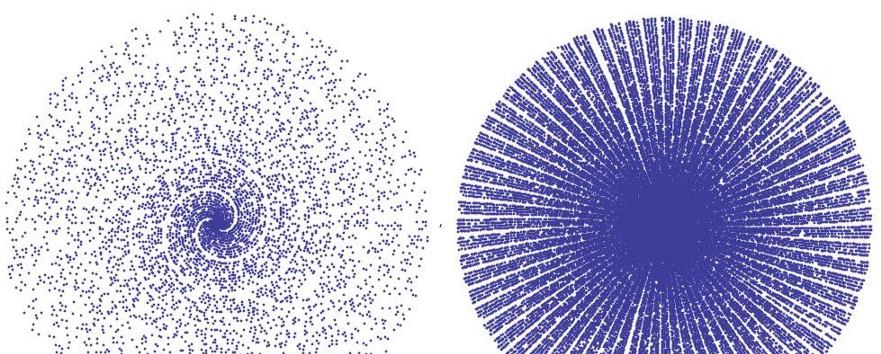
图1：在极坐标下5000和50000质数的比较 。 应该注意1不是质数 。 但是为什么1不是质数呢？实际上 ， 直到20世纪 ， 1一直被认为是质数 。 于是数学家们选择不接受1是质数 ， 这样就能更容易地写出很多定理 。 根据质数的新定义 ， 它们不再用1作为质数 。
此外 ， 没有因数并不是质数如此独特的唯一原因 。 例如 ， 整个数轴只用素数就可以产生 。 换句话说 ， 每一个数都可以通过质数相乘得到 。 因此 ， 我们可以很容易地说质数是数列的原子 ， 所有其他正整数都是由质数构成的 。 伟大的数学家已经证明：任何整数都可以表示为质数的乘积 。 这个理论来自于数论：算术基本定理 。 理解算术的基本原理是解开素数之谜的第一把钥匙 。
算术基本定理(欧几里德)：每一个整数P > 1都可以被唯一地写成有限素数的乘积 。
要么是素数本身 ， 要么可以表示为素数的乘积 ， 而且 ， 这种表示是唯一的 ， 除了因子的顺序 。
例如：
666 = 2 * 3 * 3 * 37 = 2 * 3^2*37
1234567890 = 2 * 3 * 3 * 5 * 3607 * 3803 = 2*3^2*5 * 3607 * 3803
基本上 ， 我们把任意一个数分解成两个数 ， 然后尽可能地把它们分解成两个质数 ， 以此类推 。 当不能再因式分解时 ， 所有剩下的数都是质数 。 最终只剩下质数 。 乘积中的项叫做质因数 。 不要忘记 ， 因素可能会出现不止一次 。
欧几里得的算术基本定理是不接受1为质数的主要原因 。 例如 ， 我们假设1是质数 。 如果我们对55做质因数分解 ， 我们得到:
55 = 11·5·1·1·1·1·1·1·1……·1 。
我们需要把上面的定理改为:“每个正整数都可以被唯一地写成质数的乘积 ， 除了无限乘以1 。 ”
推论：2的平方根是无理数 。
证明：我们假设根号2 = a/b 。
然后b xsqrt（2） = a 。 因此(b^2)*2 = a
现在假设 ， 上面方程式左侧的因子2具有奇数指数 ， 而在右侧具有偶数指数 ， 这与算术基本定理矛盾 。
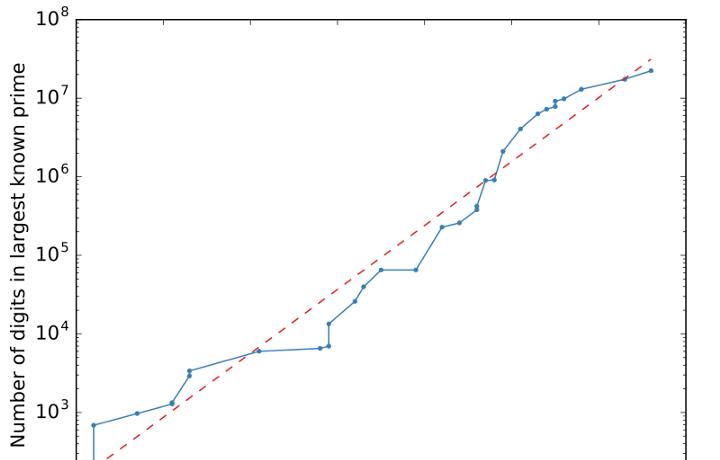
有无数个素数 。
数轴上有多少质数？无限或有限？我们知道 ， 质数只能被自身和1整除 ， 它们不能被分成更小的整数 。 所以 ， 我们能把所有可能的数字的一半从数表中去掉吗？是的 ， 可以！根据定义 ， 除了2以外的偶数不能是质数 。 同样 ， 我们可以去掉3、4、5、6、7、8的倍数 ， 等等 。 在这一点上 ， 年轻的数学家可能会想“那么就没有质数了 。 然而 ， 这不是真的 。 因为欧几里得在2300年前就证明了质数是无限的而最大的质数是不存在的 。


推荐阅读


上一篇：「银河系」8张图带你领略70亿年后的星空

下一篇：「」为啥大西洋和太平洋的海水，无法相互融合在一起？