文章插图
这三个模版的不同之处在于:
- 左、中、右索引的分配
- 循环或递归终止条件
- 后处理的必要性
这 3 个模板中的每一个都提供了一个特定的用例:
模板 1 (left <= right)
- 二分查找的最基础和最基本的形式 。
- 查找条件可以在不与元素的两侧进行比较的情况下确定(或使用它周围的特定元素) 。
- 不需要后处理,因为每一步中,你都在检查是否找到了元素 。如果到达末尾,则知道未找到该元素 。
- 一种实现二分查找的高级方法 。
- 查找条件需要访问元素的直接右邻居 。
- 使用元素的右邻居来确定是否满足条件,并决定是向左还是向右 。
- 保证查找空间在每一步中至少有 2 个元素 。
- 需要进行后处理 。当你剩下 1 个元素时,循环 / 递归结束 。需要评估剩余元素是否符合条件 。
- 实现二分查找的另一种方法 。
- 搜索条件需要访问元素的直接左右邻居 。
- 使用元素的邻居来确定它是向右还是向左 。
- 保证查找空间在每个步骤中至少有 3 个元素 。
- 需要进行后处理 。当剩下 2 个元素时,循环 / 递归结束 。需要评估其余元素是否符合条件 。
O(log n) :
因为二分查找是通过对查找空间中间的值应用一个条件来操作的,并因此将查找空间折半,在更糟糕的情况下,我们将不得不进行O(log n) 次比较,其中n是集合中元素的数目 。
为什么是log n?
- 二分查找是通过将现有数组一分为二来执行的
- 因此,每次调用子例程(或完成一次迭代)时,其大小都会减少到现有部分的一半 。
- 首先N变成 N/2,然后又变成N/4,然后继续下去,直到找到元素或尺寸变为1 。
- 迭代的最大次数是log N(base2) 。
第一次: n/2第二次: n/2^2第三次: n/2^3...第k次: n/2^k
文章插图

文章插图
3.2、空间复杂度
O(1)
虽然二分查找确实需要跟踪 3 个指标,但迭代解决方案通常不需要任何其他额外空间,并且可以直接应用于集合本身,因此需要 O(1) 或常量空间 。
四、二分查找的应用
- 二分调试法
通过二分法,我们可以快速缩小问题范围,这样一来调试的效率也就上去了 。
- Kafka 采用二分法找数据

文章插图
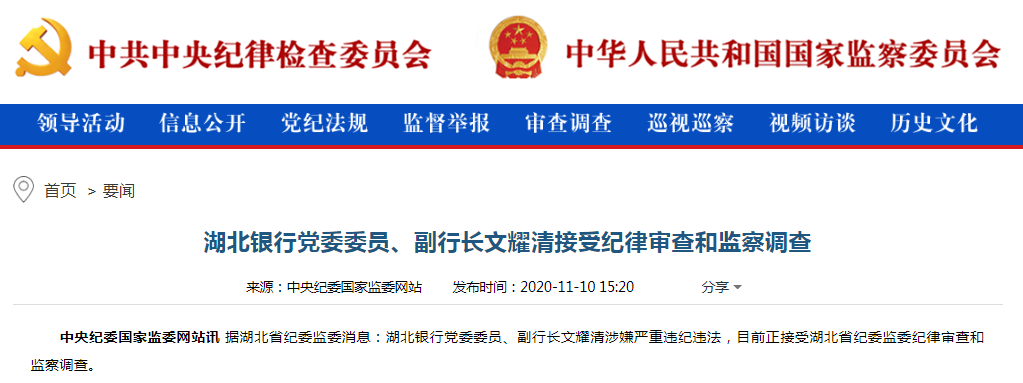
【大厂高级程序员必备算法,看似简单的二分查找,您了解多少?】
推荐阅读
- 什么香水好闻还不烂大街?这几瓶国货被公认好闻!关键高级还平价
- 穿衣搭配|职场女人该怎样穿最高级?这四种搭配方式需要掌握
- 一个程序员的水平能差到什么程度,程序员水平难判断-程序员的6大等级,赶紧对号入座吧!-
- 周南南|职场妈妈通勤怎么穿?学习周南南,高级干练值得借鉴!
- 日本|21万人!逃离大厂,涌向何处?
- 程序员|《甄嬛传》中的经典台词,道出职场潜规则,一个比一个经典
- 二战德国高级将领,二战德军一级上将-
- 和程序员谈恋爱是什么样的体验,程序员和程序员谈恋爱合适吗-
- 程序员|俄罗斯程序员开发 著名压缩软件7Zip被抵制:伪开源、还有后门
- 香港小姐|一头利落“短发”的她,凭什么美得高级?看过她的穿搭,就明白了