Sutton 强化学习,21 点游戏的策略蒙特卡洛值预测( 三 )
对于 First-visit 来说 , 当状态 s 第一次出现时计算一次 Returns , 若继续出现状态 s 不再重复计算 。 对于 Every-visit 来说 , 每次出现 s 计算一次 Returns(s) 。 举个例子 , 某 episode 数据如下:
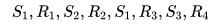 文章插图
文章插图
First-visit 对于状态 S1 的 Returns 计算为
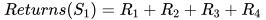 文章插图
文章插图
Every-visit 对于状态 S1 的 Returns 计算了两次 , 因为 S1 出现了两次 。
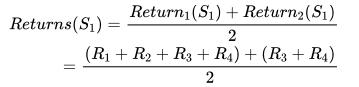 文章插图
文章插图
下面用 Monte Carlo 来模拟解得书中示例玩家固定策略的 V值 , 策略具体为:加牌直到手中点数>=20 , 代码为
def fixed_policy(observation): """ sticks if the player score is >= 20 and hits otherwise. """ score, dealer_score, usable_ace = observation return 0 if score >= 20 else 1 文章插图
文章插图
First-visit MC Predicition伪代码如下 , 注意考虑到实现上的高效性 , 在遍历 episode 序列数据时是从后向前扫的 , 这样可以边扫边更新 G 。
 文章插图
文章插图
对应的 python 实现
def mc_prediction_first_visit(policy: DeterministicPolicy, env: BlackjackEnv, num_episodes, discount_factor=1.0) -> StateValue: returns_sum = defaultdict(float) returns_count = defaultdict(float) for episode_i in range(1, num_episodes + 1): episode_history = gen_episode_data(policy, env) G = 0 for t in range(len(episode_history) - 1, -1, -1): s, a, r = episode_history[t] G = discount_factor * G + r if not any(s_a_r[0] == s for s_a_r in episode_history[0: t]): returns_sum[s] += G returns_count[s] += 1.0 V = defaultdict(float) V.update({s: returns_sum[s] / returns_count[s] for s in returns_sum.keys}) return V 文章插图
文章插图
Every-visit MC PredicitonEvery-visit 代码实现相对更简单一些 , t 从后往前遍历时更新对应 s 的状态变量 。 如下所示
def mc_prediction_every_visit(policy: DeterministicPolicy, env: BlackjackEnv, num_episodes, discount_factor=1.0) -> StateValue: returns_sum = defaultdict(float) returns_count = defaultdict(float) for episode_i in range(1, num_episodes + 1): episode_history = gen_episode_data(policy, env) G = 0 for t in range(len(episode_history) - 1, -1, -1): s, a, r = episode_history[t] G = discount_factor * G + r returns_sum[s] += G returns_count[s] += 1.0 V = defaultdict(float) V.update({s: returns_sum[s] / returns_count[s] for s in returns_sum.keys})
推荐阅读
- 计算机专业大一下学期,该选择学习Java还是Python
- 假期弯道超车 国美学习“神器”助孩子变身“学霸”
- 想自学Python来开发爬虫,需要按照哪几个阶段制定学习计划
- 未来想进入AI领域,该学习Python还是Java大数据开发
- Google AI建立了一个能够分析烘焙食谱的机器学习模型
- 学习大数据是否需要学习JavaEE
- 学习“时代楷模”精神 信息科技创新助跑5G智慧港口
- 非计算机专业的本科生,想利用寒假学习Python,该怎么入手
- ?优学天下带着学习机冲刺上市,智能教育硬件有多烧钱?
- 数据分析与机器学习:侦测应用内机器人作弊关键