дҪҝз”Ёtensorflowе’ҢKerasзҡ„еҲқзә§ж•ҷзЁӢ( дәҢ )
еҲҶзұ»й—®йўҳйҖҡеёёдҪҝз”ЁдәҢеҲҶзұ»дәӨеҸүзҶөгҖҒеӨҡеҲҶзұ»дәӨеҸүзҶөжҲ–зЁҖз–ҸеҲҶзұ»дәӨеҸүзҶө гҖӮ дәҢеҲҶзұ»дәӨеҸүзҶөз”ЁдәҺдәҢеҲҶзұ» пјҢ иҖҢеӨҡеҲҶзұ»жҲ–зЁҖз–ҸеҲҶзұ»дәӨеҸүзҶөз”ЁдәҺеӨҡзұ»еҲҶзұ»й—®йўҳ гҖӮ дҪ еҸҜд»ҘеңЁдёӢйқўзҡ„й“ҫжҺҘдёӯжүҫеҲ°жңүе…іжҚҹеӨұеҮҪж•°зҡ„жӣҙеӨҡиҜҰз»ҶдҝЎжҒҜ гҖӮ
жіЁпјҡеҲҶзұ»дәӨеҸүзҶөз”ЁдәҺеӣ еҸҳйҮҸзҡ„one-hotиЎЁзӨә пјҢ еҪ“ж ҮзӯҫдҪңдёәж•ҙж•°жҸҗдҫӣж—¶ пјҢ дҪҝз”ЁзЁҖз–ҸеҲҶзұ»дәӨеҸүзҶө гҖӮ
з”ЁPythonејҖеҸ‘ANNжҲ‘们е°ҶдҪҝз”ЁKaggleзҡ„дҝЎз”Ёж•°жҚ®ејҖеҸ‘дёҖдёӘдҪҝз”ЁJupyter Notebookзҡ„ж¬әиҜҲжЈҖжөӢжЁЎеһӢ гҖӮ еҗҢж ·зҡ„ж–№жі•д№ҹеҸҜд»ҘеңЁgoogle colabдёӯе®һзҺ° гҖӮ
ж•°жҚ®йӣҶеҢ…еҗ«2013е№ҙ9жңҲ欧жҙІжҢҒеҚЎдәәйҖҡиҝҮдҝЎз”ЁеҚЎиҝӣиЎҢзҡ„дәӨжҳ“ гҖӮ жӯӨж•°жҚ®йӣҶжҳҫзӨәдёӨеӨ©еҶ…еҸ‘з”ҹзҡ„дәӨжҳ“ пјҢ е…¶дёӯ284807笔дәӨжҳ“дёӯжңү492е®—ж¬әиҜҲ гҖӮ ж•°жҚ®йӣҶй«ҳеәҰдёҚе№іиЎЎ пјҢ жӯЈзұ»(ж¬әиҜҲ)еҚ жүҖжңүдәӨжҳ“зҡ„0.172% гҖӮ
import tensorflow as tfprint(tf.__version__)import pandas as pdimport numpy as npfrom sklearn.model_selection import train_test_splitimport tensorflow as tffrom sklearn import preprocessingfrom tensorflow.keras.models import Sequentialfrom tensorflow.keras.layers import Dense, Dropout, BatchNormalizationfrom sklearn.metrics import accuracy_score, confusion_matrix, precision_score, recall_score, f1_score, precision_recall_curve, aucimport matplotlib.pyplot as pltfrom tensorflow.keras import optimizersimport seaborn as snsfrom tensorflow import kerasimport random as rnimport osos.environ["CUDA_VISIBLE_DEVICES"] = "3"PYTHONHASHSEED=0tf.random.set_seed(1234)np.random.seed(1234)rn.seed(1254)ж•°жҚ®йӣҶз”ұд»ҘдёӢеұһжҖ§з»„жҲҗ гҖӮ ж—¶й—ҙгҖҒдё»иҰҒжҲҗеҲҶгҖҒйҮ‘йўқе’Ңзұ»еҲ« гҖӮ жӣҙеӨҡдҝЎжҒҜиҜ·и®ҝй—®KaggleзҪ‘з«ҷ гҖӮ
file = tf.keras.utilsraw_df = pd.read_csv(вҖҳ')raw_df.head()з”ұдәҺеӨ§еӨҡж•°еұһжҖ§йғҪжҳҜдё»жҲҗеҲҶ пјҢ жүҖд»Ҙзӣёе…іжҖ§жҖ»жҳҜ0 гҖӮ е”ҜдёҖеҸҜиғҪеҮәзҺ°ејӮеёёеҖјзҡ„еҲ—жҳҜamount гҖӮ дёӢйқўз®ҖиҰҒд»Ӣз»ҚдёҖдёӢиҝҷж–№йқўзҡ„з»ҹи®Ўж•°жҚ® гҖӮ
count284807.00mean88.35std250.12min0.0025%5.6050%22.0075%77.16max25691.16Name: Amount, dtype: float64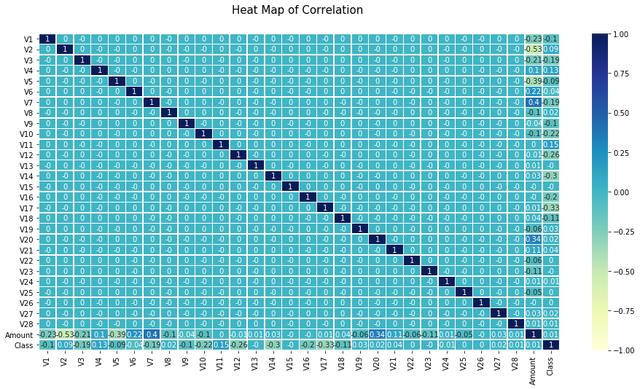 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
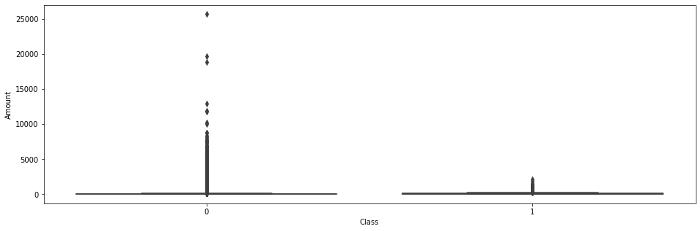
ејӮеёёеҖјеҜ№дәҺжЈҖжөӢж¬әиҜҲиЎҢдёәиҮіе…ійҮҚиҰҒ пјҢ еӣ дёәеҹәжң¬еҒҮи®ҫжҳҜ пјҢ иҫғй«ҳзҡ„дәӨжҳ“йҮҸеҸҜиғҪжҳҜж¬әиҜҲжҙ»еҠЁзҡ„иҝ№иұЎ гҖӮ 然иҖҢ пјҢ з®ұзәҝеӣҫ并没жңүжҸӯзӨәд»»дҪ•е…·дҪ“зҡ„и¶ӢеҠҝжқҘйӘҢиҜҒдёҠиҝ°еҒҮи®ҫ гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
еҮҶеӨҮиҫ“е…Ҙиҫ“еҮәе’Ңи®ӯз»ғжөӢиҜ•ж•°жҚ®X_data = http://kandian.youth.cn/index/credit_data.iloc[:, :-1]y_data = credit_data.iloc[:, -1]X_train, X_test, y_train, y_test = train_test_split(X_data, y_data, test_size = 0.2, random_state = 7)X_train = preprocessing.normalize(X_train)ж•°йҮҸе’Ңдё»жҲҗеҲҶеҲҶжһҗеҸҳйҮҸдҪҝз”ЁдёҚеҗҢзҡ„е°әеәҰ пјҢ еӣ жӯӨж•°жҚ®йӣҶжҳҜж ҮеҮҶеҢ–зҡ„ гҖӮ ж ҮеҮҶеҢ–еңЁжўҜеәҰдёӢйҷҚдёӯиө·зқҖйҮҚиҰҒдҪңз”Ё гҖӮ ж ҮеҮҶеҢ–ж•°жҚ®зҡ„收ж•ӣйҖҹеәҰиҰҒеҝ«еҫ—еӨҡ гҖӮ
print(X_train.shape)print(X_test.shape)print(y_train.shape)print(y_test.shape)иҫ“еҮәпјҡ
(227845, 29) #и®°еҪ•ж•°xеҲ—ж•°(56962, 29)(227845,)(56962,)ејҖеҸ‘зҘһз»ҸзҪ‘з»ңеұӮдёҠйқўзҡ„иҫ“еҮәиЎЁжҳҺжҲ‘们жңү29дёӘиҮӘеҸҳйҮҸиҰҒеӨ„зҗҶ пјҢ еӣ жӯӨиҫ“е…ҘеұӮзҡ„еҪўзҠ¶жҳҜ29 гҖӮ д»»дҪ•дәәе·ҘзҘһз»ҸзҪ‘з»ңжһ¶жһ„зҡ„дёҖиҲ¬з»“жһ„жҰӮиҝ°еҰӮдёӢ гҖӮ
+----------------------------+----------------------------+ |Hyper Parameter|Binary Classification| +----------------------------+----------------------------+ | # input neurons| One per input feature| | # hidden layers| Typically 1 to 5| | # neurons per hidden layer | Typically 10 to 100| | # output neurons| 1 per prediction dimension | | Hidden activation| ReLU, Tanh, sigmoid| | Output layer activation| Sigmoid| | Loss function| Binary Cross Entropy| +----------------------------+----------------------------++-----------------------------------+----------------------------+ |Hyper Parameter| Multiclass Classification| +-----------------------------------+----------------------------+ | # input neurons| One per input feature| | # hidden layers| Typically 1 to 5| | # neurons per hidden layer| Typically 10 to 100| | # output neurons| 1 per prediction dimension | | Hidden activation| ReLU, Tanh, sigmoid| | Output layer activation| Softmax| | Loss function| "Categorical Cross Entropy | | Sparse Categorical Cross Entropy" || +-----------------------------------+----------------------------+
жҺЁиҚҗйҳ…иҜ»
- Biogenе°ҶдҪҝз”ЁApple Watchз ”з©¶иҖҒе№ҙз—ҙе‘Ҷз—Үзҡ„ж—©жңҹз—ҮзҠ¶
- Eyeware BeamдҪҝз”ЁiPhoneиҝҪиёӘзҺ©е®¶еңЁжёёжҲҸдёӯзҡ„зңјзқӣиҝҗеҠЁ
- жҲ–дҪҝз”ЁеӨ©зҺ‘1000+иҠҜзүҮпјҹиҚЈиҖҖV40е·Іе…Ёжё йҒ“ејҖеҗҜйў„зәҰ
- иӢ№жһңе°ҶжҺЁеҮәдҪҝз”Ёmini LEDеұҸзҡ„iPad Pro
- жүӢжңәиғҪз”ЁеӨҡд№…пјҹеҰӮжһңеҮәзҺ°иҝҷ3з§ҚеҫҒе…ҶпјҢиҜҙжҳҺвҖңй»ҳи®ӨдҪҝз”Ёж—¶й—ҙвҖқе·ІеҲ°
- иӢ№жһңжңүжңӣеңЁ2021е№ҙеҲқеҸ‘еёғйҰ–ж¬ҫдҪҝз”Ёmini LEDжҳҫзӨәеұҸзҡ„ iPad Pro
- 笔记жң¬дҝқе…»жңүеҰҷжӢӣпјҒеӯҰдјҡиҝҷеҮ жӢӣ笔记жң¬еҶҚжҲҳдёүе№ҙ
- ж•°жҚ®еҸҜи§ҶеҢ–дёүиҠӮиҜҫд№ӢдәҢпјҡеҸҜи§ҶеҢ–зҡ„дҪҝз”Ё
- зҙўе°јsw77дёҺsw55зҡ„дҪҝз”Ёе·®еҲ«ж„ҹеҸ—
- зҲҶж–ҷз§°дёҖеҠ 9зі»еҲ—дёҺжҪңжңӣејҸй•ңеӨҙж— зјҳ 继з»ӯдҪҝз”Ёжҷ®йҖҡй•ҝз„Ұ