дәҢеҸүж ‘пјҡе…¬е…ұзҘ–е…Ҳй—®йўҳ( дәҢ )
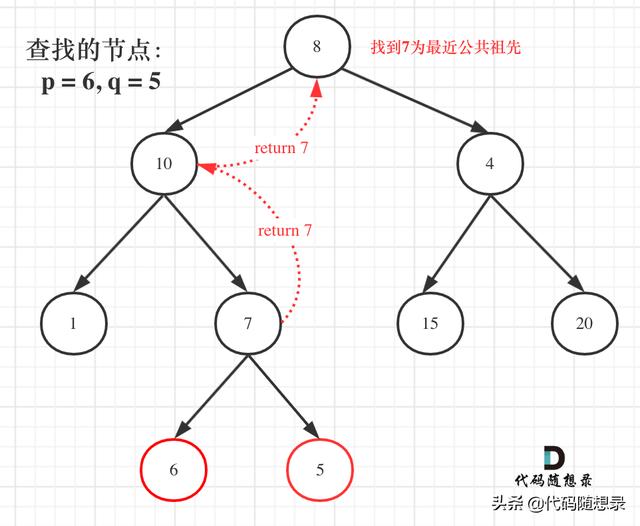
еҰӮеӣҫпјҡ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
е°ұеғҸеӣҫдёӯдёҖж ·зӣҙжҺҘиҝ”еӣһ7 пјҢ еӨҡзҫҺж»Ӣж»Ӣ гҖӮ
дҪҶдәӢе®һдёҠиҝҳиҰҒйҒҚеҺҶж №иҠӮзӮ№еҸіеӯҗж ‘пјҲеҚідҪҝжӯӨж—¶е·Із»ҸжүҫеҲ°дәҶзӣ®ж ҮиҠӮзӮ№дәҶпјү пјҢ д№ҹе°ұжҳҜеӣҫдёӯзҡ„иҠӮзӮ№4гҖҒ15гҖҒ20 гҖӮ
еӣ дёәеңЁеҰӮдёӢд»Јз Ғзҡ„еҗҺеәҸйҒҚеҺҶдёӯ пјҢ еҰӮжһңжғіеҲ©з”Ёleftе’ҢrightеҒҡйҖ»иҫ‘еӨ„зҗҶ пјҢдёҚиғҪз«ӢеҲ»иҝ”еӣһ пјҢ иҖҢжҳҜиҰҒзӯүleftдёҺrightйҖ»иҫ‘еӨ„зҗҶе®Ңд№ӢеҗҺжүҚиғҪиҝ”еӣһ гҖӮ
left = йҖ’еҪ’еҮҪж•°(root->left);right = йҖ’еҪ’еҮҪж•°(root->right);leftдёҺrightзҡ„йҖ»иҫ‘еӨ„зҗҶ;жүҖд»ҘжӯӨж—¶еӨ§е®¶иҰҒзҹҘйҒ“жҲ‘们иҰҒйҒҚеҺҶж•ҙжЈөж ‘ гҖӮ зҹҘйҒ“иҝҷдёҖзӮ№ пјҢ еҜ№жң¬йўҳе°ұжңүдёҖе®ҡж·ұеәҰзҡ„зҗҶи§ЈдәҶ гҖӮ
йӮЈд№Ҳе…Ҳз”Ёleftе’ҢrightжҺҘдҪҸе·Ұеӯҗж ‘е’ҢеҸіеӯҗж ‘зҡ„иҝ”еӣһеҖј пјҢ д»Јз ҒеҰӮдёӢпјҡ
TreeNode* left = lowestCommonAncestor(root->left, p, q);TreeNode* right = lowestCommonAncestor(root->right, p, q);гҖҢеҰӮжһңleft е’Ң rightйғҪдёҚдёәз©ә пјҢ иҜҙжҳҺжӯӨж—¶rootе°ұжҳҜжңҖиҝ‘е…¬е…ұиҠӮзӮ№ гҖӮ иҝҷдёӘжҜ”иҫғеҘҪзҗҶи§ЈгҖҚ
гҖҢеҰӮжһңleftдёәз©ә пјҢ rightдёҚдёәз©ә пјҢ е°ұиҝ”еӣһright пјҢ иҜҙжҳҺзӣ®ж ҮиҠӮзӮ№жҳҜйҖҡиҝҮrightиҝ”еӣһзҡ„ пјҢ еҸҚд№Ӣдҫқ然гҖҚ гҖӮ
иҝҷйҮҢжңүзҡ„еҗҢеӯҰе°ұзҗҶи§ЈдёҚдәҶдәҶ пјҢ дёәд»Җд№Ҳleftдёәз©ә пјҢ rightдёҚдёәз©ә пјҢ зӣ®ж ҮиҠӮзӮ№йҖҡиҝҮrightиҝ”еӣһе‘ўпјҹ
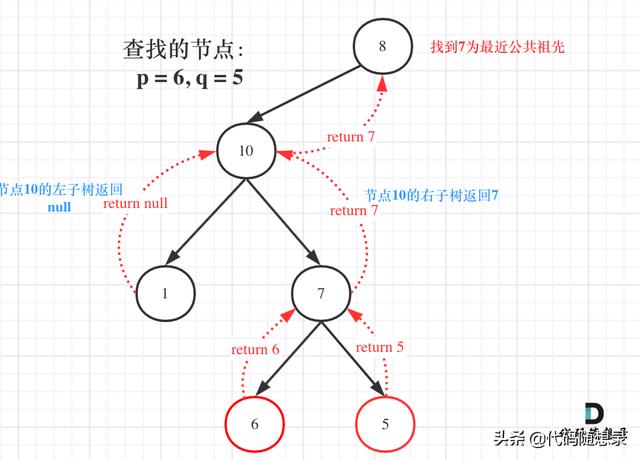
еҰӮеӣҫпјҡ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
еӣҫдёӯиҠӮзӮ№10зҡ„е·Ұеӯҗж ‘иҝ”еӣһnull пјҢ еҸіеӯҗж ‘иҝ”еӣһзӣ®ж ҮеҖј7 пјҢ йӮЈд№ҲжӯӨж—¶иҠӮзӮ№10зҡ„еӨ„зҗҶйҖ»иҫ‘е°ұжҳҜжҠҠеҸіеӯҗж ‘зҡ„иҝ”еӣһеҖјпјҲжңҖиҝ‘е…¬е…ұзҘ–е…Ҳ7пјүиҝ”еӣһдёҠеҺ»пјҒ
иҝҷйҮҢзӮ№д№ҹеҫҲйҮҚиҰҒ пјҢ еҸҜиғҪеҲ·иҝҮиҝҷйҒ“йўҳзӣ®зҡ„еҗҢеӯҰ пјҢ йғҪдёҚжё…жҘҡз»“жһң究з«ҹжҳҜеҰӮдҪ•д»Һеә•еұӮдёҖеұӮдёҖеұӮдј еҲ°еӨҙз»“зӮ№зҡ„ гҖӮ
йӮЈд№ҲеҰӮжһңleftе’ҢrightйғҪдёәз©ә пјҢ еҲҷиҝ”еӣһleftжҲ–иҖ…rightйғҪжҳҜеҸҜд»Ҙзҡ„ пјҢ д№ҹе°ұжҳҜиҝ”еӣһз©ә гҖӮ
д»Јз ҒеҰӮдёӢпјҡ
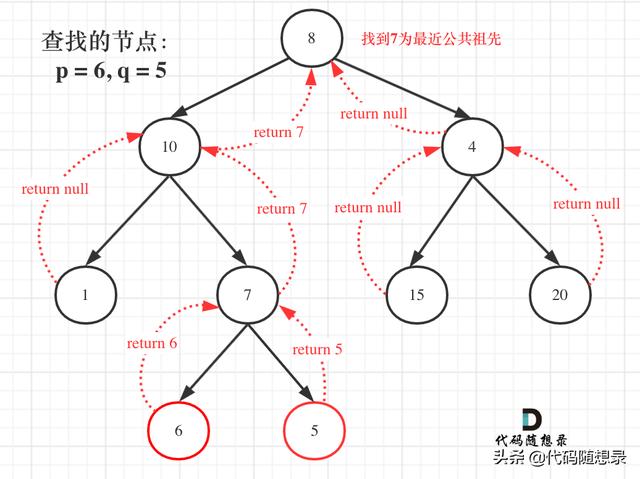
if (left == NULL else if (left != NULL else{ //(left == NULL }йӮЈд№ҲеҜ»жүҫжңҖе°Ҹе…¬е…ұзҘ–е…Ҳ пјҢ е®Ңж•ҙжөҒзЁӢеӣҫеҰӮдёӢпјҡ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
гҖҢд»Һеӣҫдёӯ пјҢ еӨ§е®¶еҸҜд»ҘзңӢеҲ° пјҢ жҲ‘们жҳҜеҰӮдҪ•еӣһжәҜйҒҚеҺҶж•ҙйў—дәҢеҸүж ‘ пјҢ е°Ҷз»“жһңиҝ”еӣһз»ҷеӨҙз»“зӮ№зҡ„пјҒгҖҚ
ж•ҙдҪ“д»Јз ҒеҰӮдёӢпјҡ
class Solution {public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (root == q || root == p || root == NULL) return root;TreeNode* left = lowestCommonAncestor(root->left, p, q);TreeNode* right = lowestCommonAncestor(root->right, p, q);if (left != NULLif (left == NULLelse if (left != NULLelse{ //(left == NULL}}};зЁҚеҠ зІҫз®Җ пјҢ д»Јз ҒеҰӮдёӢпјҡ
class Solution {public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (root == q || root == p || root == NULL) return root;TreeNode* left = lowestCommonAncestor(root->left, p, q);TreeNode* right = lowestCommonAncestor(root->right, p, q);if (left != NULLif (left == NULL) return right;return left;}};жҖ»з»“иҝҷйҒ“йўҳзӣ®еҲ·иҝҮзҡ„еҗҢеӯҰжңӘеҝ…зңҹжӯЈдәҶи§ЈиҝҷйҮҢйқўеӣһжәҜзҡ„иҝҮзЁӢ пјҢ д»ҘеҸҠз»“жһңжҳҜеҰӮдҪ•дёҖеұӮдёҖеұӮдј дёҠеҺ»зҡ„ гҖӮ
гҖҢйӮЈд№ҲжҲ‘з»ҷеӨ§е®¶еҪ’зәіеҰӮдёӢдёүзӮ№гҖҚпјҡ
- жұӮжңҖе°Ҹе…¬е…ұзҘ–е…Ҳ пјҢ йңҖиҰҒд»Һеә•еҗ‘дёҠйҒҚеҺҶ пјҢ йӮЈд№ҲдәҢеҸүж ‘ пјҢ еҸӘиғҪйҖҡиҝҮеҗҺеәҸйҒҚеҺҶпјҲеҚіпјҡеӣһжәҜпјүе®һзҺ°д»ҺдҪҺеҗ‘дёҠзҡ„йҒҚеҺҶж–№ејҸ гҖӮ
- еңЁеӣһжәҜзҡ„иҝҮзЁӢдёӯ пјҢ еҝ…然иҰҒйҒҚеҺҶж•ҙйў—дәҢеҸүж ‘ пјҢ еҚідҪҝе·Із»ҸжүҫеҲ°з»“жһңдәҶ пјҢ дҫқ然иҰҒжҠҠе…¶д»–иҠӮзӮ№йҒҚеҺҶе®Ң пјҢ еӣ дёәиҰҒдҪҝз”ЁйҖ’еҪ’еҮҪж•°зҡ„иҝ”еӣһеҖјпјҲд№ҹе°ұжҳҜд»Јз Ғдёӯзҡ„leftе’ҢrightпјүеҒҡйҖ»иҫ‘еҲӨж–ӯ гҖӮ
- иҰҒзҗҶи§ЈеҰӮжһңиҝ”еӣһеҖјleftдёәз©ә пјҢ rightдёҚдёәз©әдёәд»Җд№ҲиҰҒиҝ”еӣһright пјҢ дёәд»Җд№ҲеҸҜд»Ҙз”Ёиҝ”еӣһrightдј з»ҷдёҠдёҖеұӮз»“жһң гҖӮ
жҺЁиҚҗйҳ…иҜ»
- еӨ§дј—еұ•зӨәEVе…¬е…ұе……з”өж–°и§ЈеҶіж–№жЎҲпјҡ移еҠЁе……з”өжңәеҷЁдәә
- е……з”ө|ж–°з–Ҷе·©з•ҷеҺҝйҰ–жү№ж–°иғҪжәҗжұҪиҪҰе…¬е…ұе……з”өжЎ©жҠ•е…ҘдҪҝз”Ё
- жҷ®жёЎз§‘жҠҖеҸ‘еёғж¶ҲжҜ’жңәеҷЁдәәж¬ўд№җж¶Ҳ2пјҢеҠ©еҠӣе…¬е…ұзҺҜеўғеҚ«з”ҹ
- дёҠжө·вҖңеҚҒеӣӣдә”вҖқ规еҲ’е»әи®®пјҡе…¬е…ұйўҶеҹҹе…ЁйқўжҺЁе№ҝж–°иғҪжәҗжұҪиҪҰ
- дәҢеҸүзҠ¶жҖҒж ‘зҡ„з»“жһ„пјҢPart-1
- дәҢеҸүж ‘пјҡжұӮжҗңзҙўж ‘дёӯзҡ„дј—ж•°
- зү№ж–ҜжӢүвҖңеӨҡдәәз”өеҠЁе…¬е…ұе®ўиҪҰвҖқжёІжҹ“еӣҫ зЈҒжӮ¬жө®йҡ§йҒ“е·ҘзЁӢжӯЈеңЁиҝӣиЎҢж—¶
- дәҢеҸүж ‘пјҡжҗңзҙўж ‘зҡ„жңҖе°Ҹз»қеҜ№е·®
- дәҢеҸүж ‘пјҡдәҢеҸүжҗңзҙўж ‘зҷ»еңә
- REFIREйҮҚ塑科жҠҖеҸӮеұ•дёҠжө·еӣҪйҷ…е®ўиҪҰеұ• еҠ©еҠӣйӣ¶зўіе…¬е…ұдәӨйҖҡеҮәиЎҢ














