дәҢеҸүж ‘пјҡжҗңзҙўж ‘зҡ„жңҖе°Ҹз»қеҜ№е·®
еҲ©з”ЁдәҢеҸүжҗңзҙўж ‘зҡ„зү№жҖ§жҗһиө·пјҒ
530.дәҢеҸүжҗңзҙўж ‘зҡ„жңҖе°Ҹз»қеҜ№е·®з»ҷдҪ дёҖжЈөжүҖжңүиҠӮзӮ№дёәйқһиҙҹеҖјзҡ„дәҢеҸүжҗңзҙўж ‘ пјҢ иҜ·дҪ и®Ўз®—ж ‘дёӯд»»ж„ҸдёӨиҠӮзӮ№зҡ„е·®зҡ„з»қеҜ№еҖјзҡ„жңҖе°ҸеҖј гҖӮ
зӨәдҫӢпјҡ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
жҸҗзӨәпјҡж ‘дёӯиҮіе°‘жңү 2 дёӘиҠӮзӮ№ гҖӮ
жҖқи·Ҝйўҳзӣ®дёӯиҰҒжұӮеңЁдәҢеҸүжҗңзҙўж ‘дёҠд»»ж„ҸдёӨиҠӮзӮ№зҡ„е·®зҡ„з»қеҜ№еҖјзҡ„жңҖе°ҸеҖј гҖӮ
гҖҢжіЁж„ҸжҳҜдәҢеҸүжҗңзҙўж ‘гҖҚ пјҢ дәҢеҸүжҗңзҙўж ‘еҸҜжҳҜжңүеәҸзҡ„ гҖӮ
йҒҮеҲ°еңЁдәҢеҸүжҗңзҙўж ‘дёҠжұӮд»Җд№ҲжңҖеҖје•Ҡ пјҢ е·®еҖјд№Ӣзұ»зҡ„ пјҢ е°ұжҠҠе®ғжғіжҲҗеңЁдёҖдёӘжңүеәҸж•°з»„дёҠжұӮжңҖеҖј пјҢ жұӮе·®еҖј пјҢ иҝҷж ·е°ұз®ҖеҚ•еӨҡдәҶ гҖӮ
йҖ’еҪ’йӮЈд№ҲдәҢеҸүжҗңзҙўж ‘йҮҮз”ЁдёӯеәҸйҒҚеҺҶ пјҢ е…¶е®һе°ұжҳҜдёҖдёӘжңүеәҸж•°з»„ гҖӮ
гҖҗдәҢеҸүж ‘пјҡжҗңзҙўж ‘зҡ„жңҖе°Ҹз»қеҜ№е·®гҖ‘гҖҢеңЁдёҖдёӘжңүеәҸж•°з»„дёҠжұӮдёӨдёӘж•°жңҖе°Ҹе·®еҖј пјҢ иҝҷжҳҜдёҚжҳҜе°ұжҳҜдёҖйҒ“йҖҒеҲҶйўҳдәҶ гҖӮ гҖҚ
жңҖзӣҙи§Ӯзҡ„жғіжі• пјҢ е°ұжҳҜжҠҠдәҢеҸүжҗңзҙўж ‘иҪ¬жҚўжҲҗжңүеәҸж•°з»„ пјҢ 然еҗҺйҒҚеҺҶдёҖйҒҚж•°з»„ пјҢ е°ұз»ҹи®ЎеҮәжқҘжңҖе°Ҹе·®еҖјдәҶ гҖӮ
д»Јз ҒеҰӮдёӢпјҡ
class Solution {private:vectorд»ҘдёҠд»Јз ҒжҳҜжҠҠдәҢеҸүжҗңзҙўж ‘иҪ¬еҢ–дёәжңүеәҸж•°з»„дәҶ пјҢ е…¶е®һеңЁдәҢеҸүжҗңзҙ ж ‘дёӯеәҸйҒҚеҺҶзҡ„иҝҮзЁӢдёӯ пјҢ жҲ‘们е°ұеҸҜд»ҘзӣҙжҺҘи®Ўз®—дәҶ гҖӮ
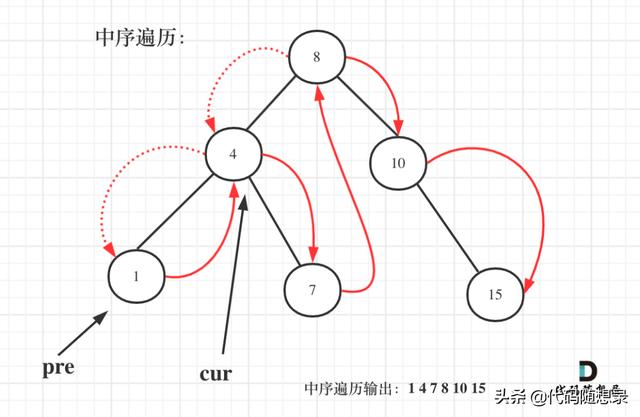
йңҖиҰҒз”ЁдёҖдёӘpreиҠӮзӮ№и®°еҪ•дёҖдёӢcurиҠӮзӮ№зҡ„еүҚдёҖдёӘиҠӮзӮ№ гҖӮ
еҰӮеӣҫпјҡ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
дёҖдәӣеҗҢеӯҰдёҚзҹҘйҒ“еңЁйҖ’еҪ’дёӯеҰӮдҪ•и®°еҪ•еүҚдёҖдёӘиҠӮзӮ№зҡ„жҢҮй’Ҳ пјҢ е…¶е®һе®һзҺ°иө·жқҘжҳҜеҫҲз®ҖеҚ•зҡ„ пјҢ еӨ§е®¶еҸӘиҰҒзңӢиҝҮдёҖж¬Ў пјҢ еҶҷиҝҮдёҖж¬Ў пјҢ е°ұжҺҢжҸЎдәҶ гҖӮ
д»Јз ҒеҰӮдёӢпјҡ
class Solution {private:int result = INT_MAX;TreeNode* pre;void traversal(TreeNode* cur) {if (cur == NULL) return;traversal(cur->left);// е·Ұif (pre != NULL){// дёӯresult = min(result, cur->val - pre->val);}pre = cur; // и®°еҪ•еүҚдёҖдёӘtraversal(cur->right);// еҸі}public:int getMinimumDifference(TreeNode* root) {traversal(root);return result;}};жҳҜдёҚжҳҜзңӢдёҠеҺ»д№ҹ并дёҚеӨҚжқӮпјҒ
иҝӯд»ЈзңӢиҝҮиҝҷдёӨзҜҮдәҢеҸүж ‘пјҡеҗ¬иҜҙйҖ’еҪ’иғҪеҒҡзҡ„ пјҢ ж Ҳд№ҹиғҪеҒҡпјҢ дәҢеҸүж ‘пјҡеүҚдёӯеҗҺеәҸиҝӯд»Јж–№ејҸзҡ„еҶҷжі•е°ұдёҚиғҪз»ҹдёҖдёҖдёӢд№Ҳпјҹ ж–Үз« д№ӢеҗҺ пјҢ дёҚйҡҫеҶҷеҮәдёӨз§ҚдёӯеәҸйҒҚеҺҶзҡ„иҝӯд»Јжі• гҖӮ
дёӢйқўжҲ‘з»ҷеҮәе…¶дёӯзҡ„дёҖз§ҚдёӯеәҸйҒҚеҺҶзҡ„иҝӯд»Јжі• пјҢ д»Јз ҒеҰӮдёӢпјҡ
class Solution {public:int getMinimumDifference(TreeNode* root) {stack st;TreeNode* cur = root;TreeNode* pre = NULL;int result = INT_MAX;while (cur != NULL || !st.empty()) {if (cur != NULL) { // жҢҮй’ҲжқҘи®ҝй—®иҠӮзӮ№ пјҢ и®ҝй—®еҲ°жңҖеә•еұӮst.push(cur); // е°Ҷи®ҝй—®зҡ„иҠӮзӮ№ж”ҫиҝӣж Ҳcur = cur->left;// е·Ұ} else {cur = st.top();st.pop();if (pre != NULL) {// дёӯresult = min(result, cur->val - pre->val);}pre = cur;cur = cur->right;// еҸі}}return result;}};жҖ»з»“гҖҢйҒҮеҲ°еңЁдәҢеҸүжҗңзҙўж ‘дёҠжұӮд»Җд№ҲжңҖеҖј пјҢ жұӮе·®еҖјд№Ӣзұ»зҡ„ пјҢ йғҪиҰҒжҖқиҖғдёҖдёӢдәҢеҸүжҗңзҙўж ‘еҸҜжҳҜжңүеәҸзҡ„ пјҢ иҰҒеҲ©з”ЁеҘҪиҝҷдёҖзү№зӮ№ гҖӮ гҖҚ
еҗҢж—¶иҰҒеӯҰдјҡеңЁйҖ’еҪ’йҒҚеҺҶзҡ„иҝҮзЁӢдёӯеҰӮдҪ•и®°еҪ•еүҚеҗҺдёӨдёӘжҢҮй’Ҳ пјҢ иҝҷд№ҹжҳҜдёҖдёӘе°ҸжҠҖе·§ пјҢ еӯҰдјҡдәҶиҝҳжҳҜеҫҲеҸ—з”Ёзҡ„ гҖӮ
еҗҺйқўжҲ‘е°Ҷ继з»ӯд»Ӣз»ҚдёҖзі»еҲ—еҲ©з”ЁдәҢеҸүжҗңзҙўж ‘зү№жҖ§зҡ„йўҳзӣ® гҖӮ
гҖҢе°ұй…ұ пјҢ ж„ҹи§үеӯҰеҲ°дәҶ пјҢ е°ұиҪ¬еҸ‘з»ҷиә«иҫ№йңҖиҰҒзҡ„еҗҢеӯҰеҗ§гҖҚ
жҺЁиҚҗйҳ…иҜ»
- дј з»ҹ1/10еӨ§е°Ҹ дёғеҪ©иҷ№еҸ‘еёғжңҖе°Ҹзҡ„mini SSDзЎ¬зӣҳпјҡжҖ§иғҪйҰ–ж¬Ўе…¬ејҖ
- Apple Fitness+ж’ӯж”ҫеҲ—иЎЁзҺ°еҸҜеңЁApple MusicжҗңзҙўдёҠжүҫеҲ°
- дё–з•ҢжңҖе°ҸжүӢжңәеҸ‘е”®пјҡ31е…Ӣ жү“зҒ«жңәйӮЈд№ҲеӨ§
- еҸ·з§°дё–з•ҢжңҖе°ҸжүӢжңәпјҒZanco Tiny T2 еҸ‘е”®
- иӢ№жһңжӯЈеңЁз ”еҸ‘зҡ„жҗңзҙўеј•ж“ҺиғҪе№Ізҡ„иҝҮи°·жӯҢеҗ—пјҹ
- йЎ№зӣ®е®һжҲҳ | и®°дёҖж¬ЎеҜ№жҹҗзҢҘзҗҗPHPеҗҺй—Ёзҡ„зҲҶиҸҠ
- жҗңжө·дҝЎеҮәеҚҺдёә еҚҺдёәжҷәж…§еұҸжҲӘдәҶвҖңжө·дҝЎвҖқ
- и°·жӯҢжҗңзҙўзҡ„зҒөйӯӮпјҒBERTжЁЎеһӢзҡ„еҙӣиө·дёҺиҚЈиҖҖ
- и°·жӯҢйҒӯзҫҺеӣҪ38е·һиҒ”еҗҲиө·иҜүйқһжі•еһ„ж–ӯеёӮеңәпјҢз§°е…¶дҫөе®ізҪ‘з»ңжҗңзҙўдёҺдҪҝз”Ёе№ҝе‘ҠдёҡеҠЎеүҘеӨәж¶Ҳиҙ№иҖ…жқғзӣҠ
- еҢ—дә¬ең°й“ҒеҲ—иҪҰе°Ҷз”ЁдёҠ5GжҠҖжңҜпјҢжңҖе°Ҹй—ҙйҡ”е°Ҷзј©зҹӯ10%