зЎ¬ж ёдёЁдёҖд»Ҫе…ідәҺж”Ҝд»ҳзҪ‘з»ңдёӯи·Ҝз”ұй—®йўҳзҡ„е…Ёйқўз ”究
ж‘ҳиҰҒпјҡ еҢәеқ—й“ҫеӣ Layer 1 зҡ„дәӨжҳ“еҗһеҗҗйҮҸдёҠйҷҗиҖҢеёёиў«иҜҹз—… пјҢ зҰ»зәҝж”Ҝд»ҳзҪ‘з»ңпјҲoff-chain payment channel network пјҢ PCNпјүжҸҗдҫӣдәҶдёҖз§ҚгҖҢзәҝдёӢж”Ҝд»ҳ+зәҝдёҠз»“з®—гҖҚзҡ„и§ЈеҶіж–№жЎҲ гҖӮ ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
еҢәеқ—й“ҫеӣ Layer 1 зҡ„дәӨжҳ“еҗһеҗҗйҮҸдёҠйҷҗиҖҢеёёиў«иҜҹз—… пјҢ зҰ»зәҝж”Ҝд»ҳзҪ‘з»ңпјҲoff-chain payment channel network пјҢ PCN пјҢ дёӢж–Үз»ҹз§°гҖҢж”Ҝд»ҳзҪ‘з»ңгҖҚпјүжҸҗдҫӣдәҶдёҖз§ҚгҖҢзәҝдёӢж”Ҝд»ҳ+зәҝдёҠз»“з®—гҖҚзҡ„и§ЈеҶіж–№жЎҲ пјҢ дёәеҢәеқ—й“ҫдё–з•Ңзҡ„ж”Ҝд»ҳпјҲеҸҠе…¶жіӣеҢ–жҲҗзҡ„еҗ„зұ»дәӨдә’пјүиөӢдәҲдәҶеҮ д№Һж— йҷҗзҡ„дәӨжҳ“еҗһеҗҗйҮҸ гҖӮ еӣ иҖҢ пјҢ ж”Ҝд»ҳзҪ‘з»ңжҲҗдёәдәҶеҪ“еүҚжңҖдёәзғӯй—Ёзҡ„еҢәеқ—й“ҫз ”з©¶дёҺе·ҘзЁӢе®һи·өж–№еҗ‘д№ӢдёҖ гҖӮ
з»ҸиҝҮеӨҡе№ҙеӣҪйҷ…еӯҰиҖ…дёҺе·ҘзЁӢзҡ„еҸ‘еұ• пјҢ ж”Ҝд»ҳзҪ‘з»ңзҡ„иӢҘе№Іеӯҗз ”з©¶ж–№еҗ‘е·ІжңүдәҶеӨ§йҮҸзҡ„и®әж–Үз ”з©¶е’Ңе·ҘзЁӢе®һи·ө пјҢ е·Із»ҸдёҚжҳ“йҒҚеҺҶйҳ…иҜ»е’ҢиҜҰе°ҪдәҶи§Ј гҖӮ 然иҖҢ пјҢ еҪ“еүҚйҳ¶ж®өеҜ№дәҺиҝҷдёҖйҮҚиҰҒзҡ„з ”з©¶ж–№еҗ‘ пјҢ иҷҪ然еӨҡж•°еҢәеқ—й“ҫйўҶеҹҹзҡ„дәәеЈ«еҜ№е…¶еҹәжң¬жҖқжғіжңүжүҖдәҶи§Ј пјҢ дҪҶеҜ№е…¶жңҖж–°иҝӣеұ•е…·жңүиҫғе…ЁйқўиҝҪиёӘзҡ„еӣҪеҶ…жһҒе®ўдёҺеӯҰиҖ…иҝҳдёҚеӨҡ гҖӮ
жң¬з»јиҝ°зі»еҲ—йқўеҗ‘еҜ№иҝҷдёҖйўҶеҹҹе…·жңүе…ҙи¶Јзҡ„жһҒе®ўе’ҢеӯҰиҖ… пјҢ еү–жһҗиӢҘе№Іеӯҗж–№еҗ‘ пјҢ еҪ’зәіжңҖж–°з ”з©¶иҝӣеұ•гҖҒжҸҗеҮә笔иҖ…зҡ„жҖқиҖғ гҖӮ дҪңиҖ…жҳҜзғӯзҲұз ”з©¶зҡ„ Nervos е°Ҹдјҷдјҙ Shor пјҢ зҺ°дёәдёҠжө·дәӨйҖҡеӨ§еӯҰеҚҡеЈ« гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
жң¬ж–Үдёӯ пјҢ жҲ‘们й»ҳи®ӨиҜ»иҖ…е…·еӨҮдәҶеҜ№дәҺж”Ҝд»ҳзҪ‘з»ңпјҲoff-chain payment networkпјүзҡ„еҹәжң¬дәҶи§Ј гҖӮ еңЁйғЁеҲҶжҸҸиҝ°дёӯ пјҢ жҲ‘们дјҡе°Ҷж”Ҝд»ҳзҪ‘з»ңзңӢдҪңдёҖеј еӣҫи®әж„Ҹд№үдёҠзҡ„еӣҫпјҲgraphпјү пјҢ жҜҸдёӘеҸӮдёҺиҖ…зңӢдҪңдёҖдёӘиҠӮзӮ№пјҲvertexпјү пјҢ жҜҸдёӘж”Ҝд»ҳйҖҡйҒ“зңӢдҪңдёҖжқЎеӣҫдёҠзҡ„иҫ№пјҲedgeпјү гҖӮ жүҖд»ҘдёӢж–Үдёӯ笔иҖ…дјҡдёҚиҮӘи§үең°з”ЁгҖҢеӣҫгҖҚжқҘжҢҮд»ЈдёҖдёӘж”Ҝд»ҳзҪ‘з»ң пјҢ з”ЁгҖҢиҠӮзӮ№гҖҚжқҘжҢҮд»ЈдёҖдёӘеҸӮдёҺиҖ… пјҢ гҖҢиҫ№гҖҚеӯ—жқҘжҢҮд»ЈдёҖдёӘж”Ҝд»ҳйҖҡйҒ“ гҖӮ
и·Ҝз”ұ пјҢ еҚідёҖдёӘйңҖиҰҒеңЁж”Ҝд»ҳзҪ‘з»ңдёҠеҸ‘йҖҒдәӨжҳ“зҡ„дәәе’ҢдәӨжҳ“жҺҘ收иҖ…дёҺеӣҫдёҠе…¶д»–иҠӮзӮ№е…ұеҗҢдә’еҠЁиҖҢеҶіе®ҡж”Ҝд»ҳи·Ҝеҫ„зҡ„иҝҮзЁӢ гҖӮ еҪ“然 пјҢ дёҘж јиҖҢиЁҖ пјҢ иҝҷдёҚдёҖе®ҡжҳҜдёҖжқЎи·Ҝеҫ„ пјҢ иҖҢеҸҜиғҪжҳҜдёҖзі»еҲ—и·Ҝеҫ„з»„жҲҗзҡ„дёҖдёӘжңүеҗ‘ж— зҺҜеӣҫпјҲdirected acyclic graph, DAGпјү пјҢ з”ұдәҺе…¶д»–еӯҰиҖ…дјјд№Һе°ҡжңӘеҜ№жӯӨиҢғз•ҙйҮҮз”Ёж–°еҗҚиҜҚ пјҢ еӣ иҖҢ笔иҖ…е°ҶжӯӨзі»еҲ—и·Ҝеҫ„зҡ„жҖ»е’Ңе‘ҪеҗҚдёә transaction pattern гҖӮ
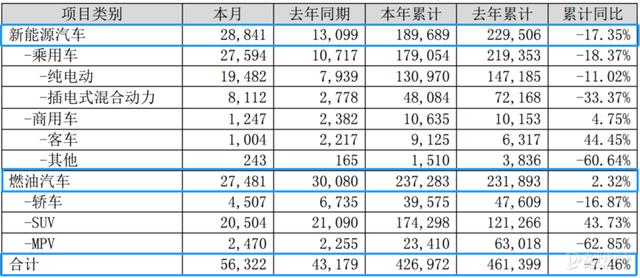
1 еҹәдәҺзҪ‘з»ңжөҒзҡ„и·Ҝз”ұеҚҸи®®
з”ЁдёҖдёӘзҪ‘з»ңжөҒжЁЎеһӢеҲ»з”»ж”Ҝд»ҳзҪ‘и·Ҝзҡ„ж•ҙдҪ“зҠ¶жҖҒе…·жңүд»ҘдёӢдјҳеҠҝпјҡйҰ–е…Ҳ пјҢ зҪ‘з»ңжөҒеҮҶзЎ®еҲ»з”»дәҶеҗ„ж”Ҝд»ҳйҖҡйҒ“зҡ„жҖ»йўқеәҰгҖҒдҪҷйҮҸ пјҢ дҪҝз”ЁзҺ°жңүзҡ„жңҖеӨ§жөҒз®—жі•еҸҜд»ҘжүҫеҲ°дёӨзӮ№д№Ӣй—ҙеҸҜд»ҘиҫҫеҲ°зҡ„жңҖеӨ§ж”Ҝд»ҳжҖ»йўқ пјҢ 并且й«ҳж•Ҳең°жүҫеҮәдёҖз»„еҸҜиЎҢи·Ҝеҫ„ гҖӮ жҺҘдёӢжқҘ пјҢ 笔иҖ…з®ҖиҰҒд»Ӣз»ҚдёҖдёӢзҪ‘з»ңжөҒй—®йўҳ гҖӮ
HintпјҡгҖҢеҹәдәҺзҪ‘з»ңжөҒзҡ„и·Ҝз”ұеҚҸи®®гҖҚжҳҜ笔иҖ…жүҖжӢҹзҡ„еҗҚз§° пјҢ е…¶еңЁеӨ§еӨҡж•°ж–ҮзҢ®дёӯеҜ№еә”зҡ„иҜҚз»„жҳҜ Source Routing гҖӮ е…¶еҺҹеӣ жҳҜиҝҷдёҖзұ»и·Ҝз”ұзҡ„иҝҮзЁӢеҫ—з”ұжәҗиҠӮзӮ№жң¬ең°е®ҢжҲҗ пјҢ е…¶иҝҮзЁӢдёӯй»ҳи®ӨжәҗиҠӮзӮ№жҺҢжҸЎдәҶж•ҙеј ж”Ҝд»ҳзҪ‘з»ңзҡ„жӢ“жү‘з»“жһ„ пјҢ 并且еҸҜд»ҘеҠЁжҖҒжҺўжөӢпјҲprobeпјүд»»ж„Ҹж”Ҝд»ҳйҖҡйҒ“дёӯзҡ„дҪҷйҮҸ гҖӮ 然иҖҢ пјҢ жүҖжңүе·Іжңүзҡ„Source Routingж–№жЎҲйғҪжҳҜеҹәдәҺжңҖеӨ§жөҒз®—жі•зҡ„ пјҢ жүҖд»Ҙ笔иҖ…еӨ§иғҶең°ж”№жҚўдәҶз§°е‘ј пјҢ д»ҘдҫҝиҜ»иҖ…зҗҶи§ЈпјҲеҸҰдёҖеӨ§еҺҹеӣ жҳҜ笔иҖ…еңЁз ”究еұ•жңӣйғЁеҲҶе°ҶжҸҗеҮәдёҖз§Қ并йқһ source routing иҢғз•ҙзҡ„еҹәдәҺзҪ‘з»ңжөҒзҡ„и·Ҝз”ұеҚҸи®®пјү гҖӮ зҪ‘з»ңжөҒй—®йўҳз®Җд»Ӣ
жҲ‘们用зҪ‘з»ңжөҒжЁЎеһӢдёӯзҡ„дёҖдёӘж®ӢйҮҸзҪ‘з»ңпјҲresidual networkпјүиЎЁиҝ°дёҖдёӘж”Ҝд»ҳзҪ‘и·Ҝзҡ„ж•ҙдҪ“зҠ¶жҖҒпјҲconfigurationпјү пјҢ е…¶жң¬иҙЁжҳҜдёҖдёӘеӣӣе…ғзҘ– пјҢе…¶дёӯжҳҜиҠӮзӮ№йӣҶеҗҲ пјҢ жҜҸдёӘиҠӮзӮ№д»ЈиЎЁдёҖдёӘж”Ҝд»ҳзҪ‘з»ңдёӯзҡ„еҸӮдёҺиҠӮзӮ№ пјҢ жҳҜиҫ№йӣҶ пјҢ жҜҸжқЎиҫ№д»ЈиЎЁдәҶдёҖдёӘж”Ҝд»ҳйҖҡйҒ“, иЎЁзӨәеҗ„иҫ№зҡ„ж®ӢдҪҷйҖҡйҮҸ гҖӮ з»“еҗҲж”Ҝд»ҳзҪ‘и·Ҝзҡ„еә”з”ЁйңҖиҰҒ пјҢ жҲ‘们дёҚеҗҢдәҺзҪ‘з»ңжөҒдј з»ҹең°еўһеҠ иЎЁзӨәеҗ„йҖҡйҒ“е»әз«Ӣд№Ӣж—¶зЎ®з«Ӣзҡ„жңҖеӨ§йҖҡйҮҸпјҲ, пјү гҖӮ
жңҖеӨ§жөҒжҳҜеңЁзҪ‘з»ңжөҒжЁЎеһӢдёҠзҡ„дёҖж—ҸзәҝжҖ§и§„еҲ’й—®йўҳ гҖӮ
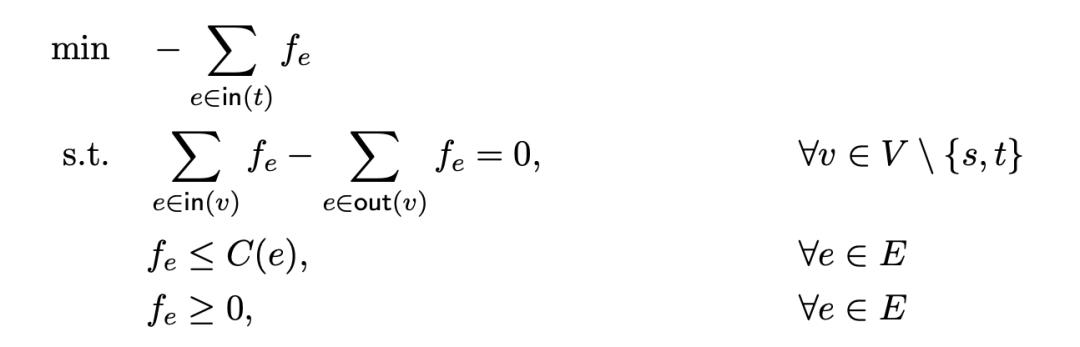 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
иҝҷдёӘеҹәдәҺзәҝжҖ§и§„еҲ’зҡ„дёҘи°Ёе®ҡд№ү并дёҚж–№дҫҝи§Ӯ众们зҗҶи§Ј гҖӮ 笔иҖ…з”»дәҶд»ҘдёӢзҡ„еӣҫзүҮжқҘеё®еҠ©иҜ»иҖ…зҗҶи§ЈжңҖеӨ§жөҒй—®йўҳзҡ„е®ҡд№ү гҖӮ дёӢеӣҫдёӯ пјҢеҲ° зҡ„жңҖеӨ§жөҒдёә еҚ•дҪҚ гҖӮ
жҺЁиҚҗйҳ…иҜ»
- й«ҳдёӢз«ӢзҺ°пјҒе…ідәҺж ёеҝғжҠҖжңҜзҡ„жҖҒеәҰпјҢжҹідј еҝ—е’Ңд»»жӯЈйқһжҲӘ然дёҚеҗҢ
- е…ідәҺжүӢжңәзҡ„и°ЈиЁҖвҖҰвҖҰеҲ«еҶҚдҝЎдәҶ
- иӢ№жһңжҖ»йғЁеӨ§жҘјпјҢж–Ҙе·Ёиө„жү“йҖ зҡ„зІҫе“Ғе»әзӯ‘пјҢжңүдҪ зҡ„дёҖд»Ҫиө„еҠ©еҗ—пјҹ
- иҝҷж¬ЎзңҹдёҚз«ҷеҚҺдёәпјҒе…ідәҺеҚҺдёәдёӢжһ¶и…ҫи®ҜжёёжҲҸдәӢ件пјҒеҚҺдёәжңүзӮ№дёҚеӨҹж„ҸжҖқ
- е…ідәҺзү№ж–ҜжӢүеүҜжҖ»иЈҒйҷ¶зҗіеҘіеЈ«еӣһеә”зҡ„еӣһеә”
- е…ідәҺе°Ҹзұі11вҖңзҺҜдҝқвҖқпјҢжҳҜжҲ‘们дҪҺдј°дәҶйӣ·еҶӣпјҢиҝҳжҳҜе°Ҹзұій«ҳдј°дәҶдәәжҖ§пјҹ
- е°Ҹзұі11жӯЈејҸеҸ‘еёғпјҢе…ідәҺйҖҒдёҚйҖҒе……з”өеҷЁпјҢйӣ·еҶӣз»ҷеҮәдәҶдёҖдёӘвҖңзҘһеҘҮвҖқзҡ„ж–№жЎҲ
- е…ЁйҮ‘еұһзЎ¬ж ёиҢғзҡ„иҝӣйҳ¶пҪңMIFOйӯ”жөӘO7еҸҢеҠЁй“Ғзңҹж— зәҝиҝҗеҠЁи“қзүҷиҖіжңә
- е…ідәҺй”Җе”®з ҙдёҮзҡ„еҚҺдёәж–°жңәпјҒеҺҹжқҘзҪ—ж°ёжө©жӣҫз»Ҹзҡ„иҜқпјҢиҝҳзңҹзҡ„жІЎжңүиҜҙй”ҷ
- йғҪеӨҹзЎ¬ж ёпјҒиҝ‘жңҹдёҠеёӮзҡ„е№іеӨҙ&е…ҘиҖіејҸиҖіеЎһеҜ№жҜ”жЁӘиҜ„