思维|AI也用思维导图:教它像人类一样高效规划( 三 )
文章图片
向实验参与者展示的矿井图(显示可能的状态簇)
4.2 推论
我们Metropolis-within-Gibbs算法进行采访 , 以接近针对 H 的贝叶斯推断 。 该方法通过从 H的后验分布中取样更新了 H的每个成分 , 在单一Metropolis-Hasting算法步骤中对所有其他成分进行训练 。 我们使用了高斯随机游走(Gaussianrandom walk)作为连续成分的建议分布(proposaldistribution) , 并使用条件CRP先验(conditional CRPprior)作为聚类任务的建议分布[7] 。 该方法可以定义为一种关于由后验定义的关于效用函数(utilityfunction)的随机爬山算法(stochastic hill climbing) 。
4.3 结果
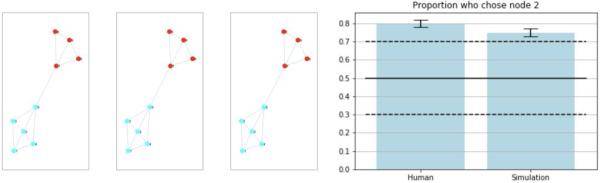
人类组和仿真组中各有32名参与者 。 前三个状态簇的模型输出结果如下图所示(左侧部分) 。 前三个结果均相同 , 表明该模型以高置信度(highconfidence)识别出彩色分组 。 参与者的结果以及静态奖励模型的结果可以从下面的条形图中(右图)看到 , 此图描述了接下来选择访问节点2的人类和模拟参与者的比例 。 实心黑线表示平均值 , 黑色虚线则表示第2.5和第97.5个百分位 。
文章图片
状态簇实验中的奖励泛化结果
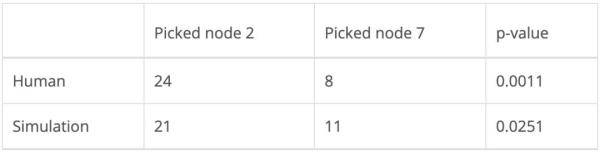
下表中列出的 p 值经右尾二项检验(right-tailed binomialtest)计算获得 , 其中null值在选择左边或右边的灰色节点时被假设为二项分布 。 显著性水平取0.05 , 人类实验结果和模型结果均具有统计学意义 。
文章图片
人类采取的行动及静态奖励模型
五、奖励催生状态簇
第二个实验的目标是确定奖励是否会催生状态簇 。 我们预测 , 即使图结构本身不会催生状态簇 , 但奖励相同的临近节点也会聚集在一起 。
Solway等人的研究发现:人类更喜欢跨越最少分层边界的路径[2] 。 因此 , 在两条完全相同的路径中做选择时 , 选中其中一条路径的唯一原因是它跨越了较少分层边界 。 对此 , 有些人可能会反驳 , 认为人们其实更倾向于选择奖励值更高的路径 。 然而 , 在接下来详述的设置方法中 , 智能体只有在实现目标时才能获得奖励 , 而不是在路径的“行走”过程中积累奖励 。 此外 , 奖励值的大小在不同的实验中也有所不同 。 因此 , 人们不太可能因为节点的奖励值更高而选择某条路径 。
5.1 设置
该实验是在网页上进行的 , 使用了亚马逊土耳其机器人(MTurk) 。 实验参与者要执行下述任务:
想象你是一名矿工 , 在由隧道连接的网状金矿中工作 。 每个矿每天会产出一定数量的黄金(用数值表示) 。 你的日常工作是从起始矿井导航到目标矿井 , 并从目标矿井内收集黄金 。 在某些时间段内 , 你可以根据喜好自由选择矿井 。 这时你应该尝试选择黄金数值最高的矿 。 在另外一些时间段 , 你只能开采一个金矿 , 该矿井的黄金数值会被标记为绿色 , 其他矿井标记为灰色 。 这时你应该导航到可开采的矿井 。 每个矿井的黄金数值都会在矿井上作标记 , 当前矿井将用粗边突出显示 。 你可以使用箭头键(上、下、左、右)在矿井间导航 。 到达目标矿井后 , 你可以按空键来收集黄金数值 , 周而复始 。 这个实验将持续100天 。
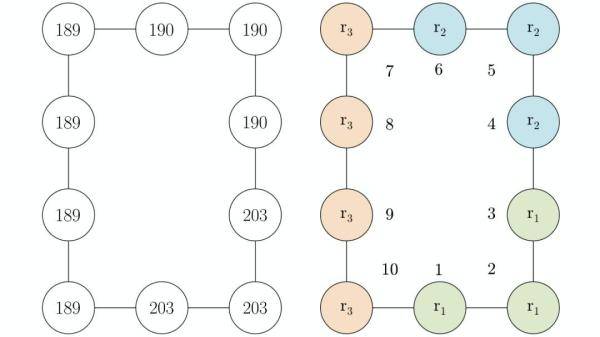
将下图(左侧部分)展现给参与者 。 与之前的实验一样 , 为了控制潜在的左右非对称性 , 我们给参与者随机分配同一图中的布局构造或水平翻转版本 , 还描述了预期催生出的状态簇 , 节点编号供参考(右侧部分) 。
文章图片
向MTurk参与者展示的矿井分布图(左)和可能存在的状态簇(右)
我们将第一种情况称为“自由选择”(free-choice) , 参与者可以自由导航到任何矿井 , 将第二种情况称为“固定选择”(fixed-choice) , 参与者需导航至指定矿井 。 为阻止随机反应 , 参与者在每次试验中都会得到金钱奖励 。
在每次试验中 , 奖励值的变化概率为0.2 , 新的奖励值从区间[0 , 300]中随机抽取 。 然而 , 奖励的分组在试验中保持不变:节点1、2和3的奖励值始终只有一个 , 节点4、5和6的奖励值不同 , 节点7、8、9和10有第三个奖励值 。
前99个试验使参与者能够建立状态簇的层次结构 , 最后一次试验(以测试试验的形式进行)要求参与者从节点6导航到节点1 。 假设奖励催生出上面所示的状态簇 , 我们预测 , 选择通过节点5的路径的参与者会比选择通过节点7的路径的参与者更多 , 因为节点5只跨越一个簇边界 , 而节点7跨越两个簇边界 。
5.2 推论
我们对固定选择案例进行建模 , 假设100个试验中的全部任务与提交给参与者的第100个试验(即测试试验)相同 。 首先 , 我们提出静态奖励假设 , 即在所有试验中奖励保持不变 。 接着 , 我们又提出动态奖励假设 , 即每次试验中奖励都会发生变化 。
推荐阅读
- 育儿说天天|孩子“脑洞”打不开、缺乏创造力!想培养,需从“思维韧性”入手
- 应急车道|媒体评“国庆期间频现应急车道被占”:有关部门懒政思维抬头
- 训练|小学三年级数学上册:思维训练题汇总!掌握好,根本不用去补习班
- 长远|训练长远思维,长远思维让自己生活有目标、行动有力量
- 中考|初中物理最全“思维导图”,26张图搞定中考物理!
- 推理小说|推理又烧脑,帮你培养缜密思维!
- 星座|这四个星座吵架时的思维,狮子座取决对方,双鱼座刁蛮任性
- 吃吃的心|仇女思维的男生到底怎么回事?
- 红楼夜思原创|从常识和思维方式的运用,看心理学对你的人生的影响
- 紧凑型SUV|“用户思维造车”的大狗,代表了新时代消费者的生活态度