高尔基|他可能是史上最尴尬诺奖得主:和死对头同台领奖,研究成果还被对方当场批评( 二 )

本文图片
高尔基 。 图片来源:Wikimedia Commons
高尔基染色法只能让 1% 到 5% 的神经细胞染色 。 由于这种不可靠的性质 , 学界对这种方法反应冷淡 , 只有很少人使用它 。 高尔基感到灰心丧气 , 转而研究疟疾 , 竟鉴定出几种不同的疟原虫 , 声名鹊起 。 多年以后 , 这种方法才在另一位科学家——卡哈尔的手中重新发扬光大 , 但高尔基本人显然对此并不高兴 。
重新发现高尔基染色法
只有少数细胞能被染色 , 这乍看之下是个缺陷 , 但在卡哈尔眼里它是个优点 。 如果所有神经细胞都被染色 , 在显微镜下看到的就会是一团乱麻 。 而使用高尔基染色法 , 被染色的细胞虽然占少数 , 但它会被整体染色 , 让卡哈尔得以观察单个神经细胞的完整结构 。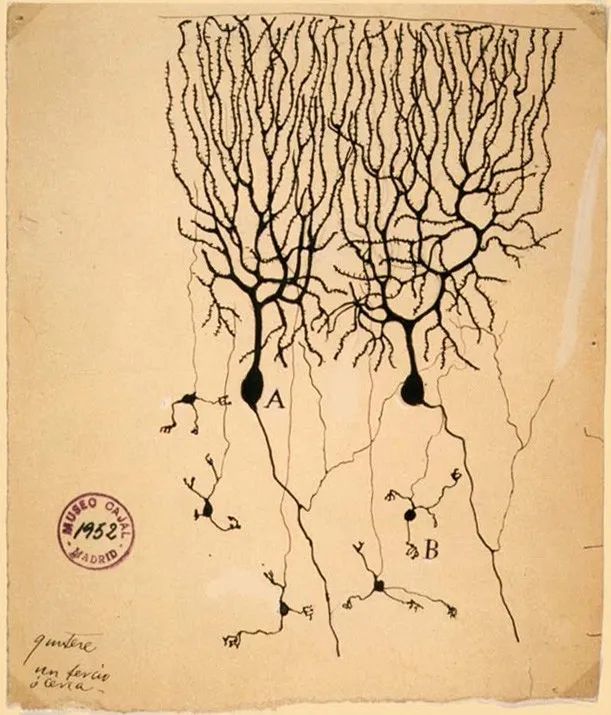
本文图片
卡哈尔作品 , 人类小脑中的浦肯野细胞 。 图片来源:Wikimedia Commons
等一下 , 神经细胞真的存在吗?
尽管早在 1865 年 , 德国科学家奥托·弗里德里希·代特(Otto Friedrich Deiters)就绘制了第一张神经细胞图片 , 但当时流行的观点认为 , 神经系统是一张错综复杂、无法分割的网 。 这就是环路理论(reticular theory) 。
高尔基也是环路理论的坚定支持者 。 在转向疟疾研究之前 , 高尔基利用这种技术绘制了大脑的多个解剖结构 。 他观察到轴突存在广泛的分叉 , 他认为这是大脑和脊髓中遍布的网状结构的基础 。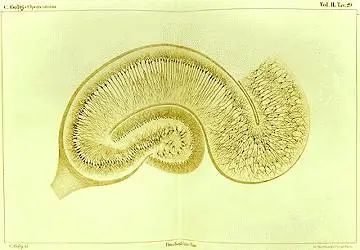
本文图片
高尔基借助自己发明的染色方法绘制的海马体 。 图片来源:Wikimedia Commons
但使用高尔基染色方法 , 卡哈尔发现事实并非如此 。 在 19 世纪 90 年代 , 他绘制了一系列精美的图片 , 表明神经元尽管形状复杂 , 它仍然符合细胞的定义 , 是独立的结构 。 他描述了神经元的胞体、树突和轴突 , 证明这些复杂精细的结构都是从胞体生长出来的 。 更重要的是 , 神经元通过突触相互连接 , 进行信号传输 , 但它们没有发生融合 , 每个神经元仍然是独立的个体 。 这就是与环路理论相对立的神经元理论(neuron theory) 。
凭借无可辩驳的证据和过人的洞察力 , 卡哈尔让学界同行纷纷放弃了环路理论 , 也为现代神经科学打下了基础 。 1906年 , 诺贝尔奖评审委员会决定将生理学和医学奖授予高尔基和卡哈尔 , 以“表彰他们在解释神经系统结构方面的研究工作” 。
和死对头同台领奖
看着自己发明的方法被用来推翻自己维护的理论 , 高尔基的心情一定十分复杂 。 在颁奖典礼上 , 高尔基先发言 , 决定再为环路理论辩论一番 。 他说:
“很奇怪 , 我一直反对神经元理论 , 但是这个理论开始得到承认还是因为我的工作 。 我选择神经元作为我的演讲主题 。 现在这个观点大体上已经不受欢迎 。 ”
接下来 , 他谈到大脑受伤后复原的能力、导航能力和整合不同功能的能力 , 他认为这些都是支持环路理论的证据 。 他还说:“尽管这和将组成元素个体化的趋势背道而驰 , 但我仍然无法放弃这个观点 , 神经系统是整体行动的 , 别怪我坚守旧观念 。 ”
面对比自己大 9 岁的前辈的公开批评 , 记录显示卡哈尔没有生气 , 而更多是尴尬 。 但他仍然不卑不亢 , 现场感谢了许多对他有帮助的人 , 并对听众们介绍了自己的工作 。 最后他说:
“没错 , 从分析工作的角度来看 , 如果所有神经中枢都由运动神经……和感觉神经之间的连续中介网络组成 , 这将是非常方便且经济的 。 不幸的是 , 大自然似乎没有意识到我们的智力对便利和统一的需求 , 而常常对复杂性和多样性感到高兴 。 ”
本文图片
卡哈尔作品 , 一个溺亡的人小脑中的浦肯野细胞 。 图片来源:卡哈尔研究所
高尔基一生反对神经元理论 , 直到 1926 年逝世 。 但以他的名字命名的解剖结构和染色方法仍然留在了教科书里 , 并且诺奖官网介绍 , 他是一位很好的老师 , 实验室永远对好奇的学生敞开大门 。 而卡哈尔后来写道 , 在分享诺奖方面 , “命运是如此残酷而讽刺……将科学上个性鲜明的对手配到了一起 。 ”
或许 , 哈卡尔和高尔基代表了两类不同的科学家 。 “科学的主要贡献者可能会发明一种新方法 , 并花费数年时间进行观察 , 描述观察结果 。 但是 , 伟大的科学家所做的不仅如此 。 他们根据研究工作 , 提出了深刻的、一致的原理 , 来解释大量数据 , 并最终证明该理论是正确的 。 ”一本高尔基传记的书评写道 。
推荐阅读
- 土豪|《变形计》史上最土豪的爸爸, 车牌遭节目组全程打码, 是真的豪门
- 科学|王莽有可能是穿越者吗?穿越时空可以实现吗?
- 明星|陈德容自曝周星驰追我时“太闷”,而且我才16岁,根本不可能
- 鲜闻联播|绫濑遥否认与鲁敏宇恋情 揭露两人近况真的没有在一起的可能吗
- 明星恋情|当红时期被告知有猝死可能,患有心脏病的黄磊,曾将妻子托付他人
- 容县之声|广西已有5人被咬伤住院!你身边也有可能出现!
- 加盟|我们的歌2:王源、郑云龙加盟,勤深深可能返场,张艺兴暂未确认
- 科学|有哪些人可能是穿越回去改变历史的?穿越时空真的可以实现吗?
- Mac|可能是Mac上最好用的键鼠套装:罗技MX Keys & MX Master 3 For Mac 使用体验
- 新冠|研究称美国洛杉矶早期新冠病毒可能主要源自欧洲

















