江苏龙网

  1. 首页 > 资讯 > 资讯 > >

楼梯|永远走不完的楼梯真的存在嘛？

如果有一天有人这样告诉你：“你可以沿着一段一直向上的台阶（或楼梯）走 ， 最终能回到出发点 。 ”你会怎样回答？单凭直觉和逻辑 ， 你可能马上会说“这绝不可能” 。 那为什么还会有人如此发问呢？说到这里 ， 我们就不得不提埃舍尔的著名版画作品《上升与下降》 ， 在这幅版画的城堡楼顶上 ， 你会看到内圈的队伍一直在下坡 ， 外圈的队伍却一直在上坡 ， 并形成一个回路 ， 周而复始 。 你能看出其中的奥秘吗？其实 ， 我们将它抽象画出来 ， 就是彭罗斯阶梯（或台阶） 。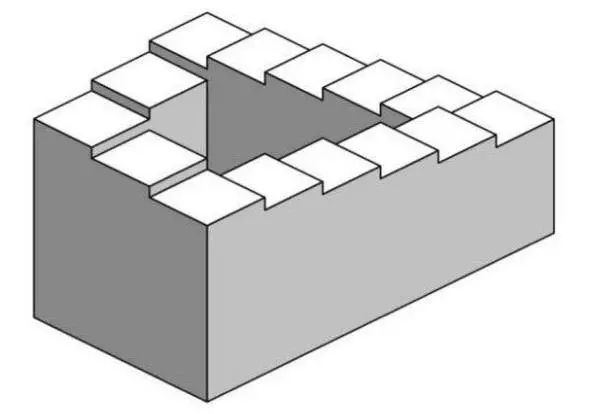
楼梯|永远走不完的楼梯真的存在嘛？
本文图片

part.1
初识彭罗斯阶梯
最早记载的彭罗斯阶梯是瑞典艺术家奥斯卡·路透·瓦德（Oscar Reutersv?rd）在1934年制作的雕塑 。 后来 ， 英国数学家、物理学家罗杰·彭罗斯（Sir Roger Penrose）和他的父亲 ， 精神病学家、遗传学家莱昂内尔·彭罗斯（Lionel Sharples Penrose）设计了多种“不可能存在”图形并进行了推广 。 1958年2月 ， 他们把这个作品发表在《英国心理学杂志》上 。 自此 ， 后续的学者将其命名为彭罗斯阶梯（Penrose Stairs） 。 据悉 ， 彭罗斯阶梯的创作也受到了荷兰画家埃舍尔（Escher）的一些“不可能存在的画作”的启发 。
楼梯|永远走不完的楼梯真的存在嘛？
本文图片

彭罗斯阶梯是著名的数学悖论之一 ， 指的是一个始终向上或向下但却无限循环的阶梯 ， 可以视为彭罗斯三角形的一个变体 ， 在此阶梯上永远无法找到最高点或者最低点 。 彭罗斯阶梯违反了欧几里得几何学的基本规则 ， 描绘了一个在三维世界（我们现在生活的世界）中不可能存在的物体 ， 即：如果一段台阶都是连续上升（或者下降）的 ， 那么整段台阶的高度就是大于零的 ， 也就不可能回到原点 。 直觉和逻辑都告诉我们被骗了 ， 但又是为什么呢？
part.2
彭罗斯阶梯的原理
楼梯|永远走不完的楼梯真的存在嘛？
本文图片

在地面上绘制的艺术品
在现实生活中 ， 我们经常能看到一些平面上绘制的立体画 。 在特定的视角观察这些立体画 ， 我们可以感受到一种三维错觉 。 比如上面这幅画 ， 从我们眼睛的角度看上去好像是三维的 ， 但其实这些画是在一个平面上制作出来的 ， 只不过是在绘画的过程中 ， 通过一些手法对细节进行了处理 ， 从而让我们产生错觉 ， 有了一种立体的感觉 。
从正面视角看 ， 地面上绘制的艺术品确实有很强的三维冲击感 ， 但是当我们变换位置 ， 这种三维的感觉就会消失 。 也就是说 ， 在二维平面上设计的三维图片 ， 在缺少第三维限制的情况下是可以轻易表现出高低不同的细节 ， 从而以假乱真 ， 让我们的眼睛产生错觉 。 而彭罗斯阶梯也是如此 。
前面我们已经说过 ， 彭罗斯阶梯可以被视为彭罗斯三角形的一个变体 ， 彭罗斯三角看起来像是一个物体 ， 由三个截面为正方形的长方体所构成 ， 三个长方体组合成为一个三角形 ， 但两长方体之间的夹角似乎又是直角 。 上述性质无法在任何一个正常三维空间的物体上实现 。 尽管彭罗斯三角在三维中不可能存在 ， 但如果从三维空间的特定角度去看 ， 其看到的图案和彭罗斯三角相同 。 比如在澳大利亚的西部东珀斯 ， 就有一座彭罗斯三角雕塑 ， 这个效果其实是三维物体在特定角度的二维投影 ， 但是人脑还在思考三维的模样 ， 因此就出现了错觉 。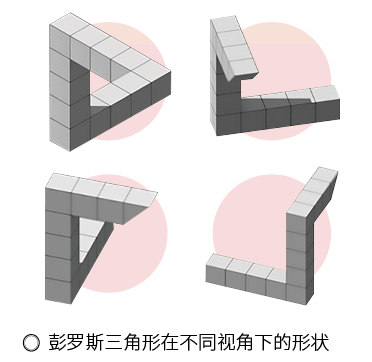
楼梯|永远走不完的楼梯真的存在嘛？
本文图片

尽管彭罗斯阶梯无法在生活中实现 ， 但我们也可以模拟这种效果 。 找一段足够长的阶梯 ， 然后每一层的阶梯要做得很宽 ， 我们可以把这些阶梯做出一定的坡度 ， 由于距离较远 ， 那些小的坡度就很不容易被人察觉到 。 每隔一段距离就做一个明显的阶梯 ， 再将这种阶梯做成蜿蜒曲折的样子 ， 然后加上一定的障碍物 ， 就可以在视觉上达到以假乱真的效果了 。
part.3
常上荧屏的彭罗斯阶梯
在一些影视作品中 ， 经常出现彭罗斯阶梯的影子 ， 比如《鬼吹灯》里的“悬魂梯”和《盗梦空间》里那个永远走不完的楼梯 。 在这些情节中 ， 关键人物走入了一圈又一圈的死循环 ， 陷入了难以摆脱的困境 。
《盗梦空间》中 ， 埃姆斯（Eames）教筑梦师爱莲（Ariadne）利用彭罗斯阶梯设计高难度的梦境 。 埃姆斯和爱莲沿着彭罗斯阶梯一直上楼 ， 每一圈都会经过那个整理文件的秘书 。 但是镜头一转 ， 埃姆斯展示了转换视角后的彭罗斯阶梯：显然中间割裂开来了 。
【楼梯|永远走不完的楼梯真的存在嘛？】楼梯|永远走不完的楼梯真的存在嘛？


推荐阅读


上一篇：将学位论文作假作为信用记录|将学位论文作假作为信用记录怎么回事？为什么要将学位论文作假作为信用记录

下一篇：|菇小毒大，食之要命