编程|数据科学家线性编程入门指南 excel|数据科学|碳水化合物

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

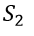
文章图片

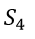
文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

介绍
优化是生活方式。我们都有有限的资源和时间，我们希望充分利用它们。从高效利用时间为公司解决供应链问题，一切都使用优化。这是数据科学中一个特别有趣。
这也是一个非常有趣的话题 - 它从简单的问题开始，但它可能会变得非常复杂。例如，在兄弟姐妹之间共享一块巧克力是一个简单的优化问题。我们在解决它时没有用数学术语来思考它。另一方面，为电子零售机制定库存和仓储策略可能非常复杂。数百万在不同地区具有不同知名度的 SKU 将在定义的时间和资源中交付 — 您认为我的意思！
线性编程（LP）是执行优化的最简单方法之一。它通过做出一些简化的假设，帮助您解决一些非常复杂的优化问题。作为分析师，您一定会遇到线性编程要解决的应用程序和问题。
出于某种原因， LP在学习数据科学时没有得到应有的。所以，我想让我为这个令人敬畏的技术伸张正义。我决定写一篇文章，用简单的英语解释线性编程。我已经尽可能简单地保留了内容。这个想法是让你开始和兴奋的线性编程。
注意-如果您想以课程形式学习，我们为你策划了这门免费课程 - 数据
内容表

什么是线性编程？

基本术语
定义 LP 问题的过程

通过图形方法求解线性程序
使用 R 求解线性程序
使用开放解算器求解线性程序
简单方法
西北角法与成本最小法
线性编程的应用

1. 什么是线性编程？
现在，什么是线性编程？线性编程是一种简单的技术，我们通过线性函数描绘复杂的关系，然后找到最佳点。前一句中的重要单词被描述出来。真正的关系可能要复杂得多，但我们可以将它们简化为线性关系。
线性编程的应用无处不在。在个人和专业方面使用线性编程。当您开车从家里去上班，并且想要走最短的路线时，您正在使用线性编程。或者，当您交付项目时，您制定策略，使团队高效工作，实现及时交付。
线性编程问题示例
假设联邦快递送货员一天有 6 个包裹要递送。仓库位于 A 点。 6 个交付目的地由 U、V、W、X、Y 和 Z 提供。线上的数字表示城市之间的距离。为了节省燃料和时间，送货员希望走最短的路线。

因此，送货员将计算前往所有 6 个目的地的不同路线，然后选择最短的路线。这种选择最短路径的技术称为线性编程。
在这种情况下，送货员的目标是在所有 6 个目的地按时递送包裹。选择最佳路径的过程称为操作研究。操作研究是一种决策方法，它涉及一套操作系统的方法。在上面的示例中，我的系统是交付模型。
线性编程用于为给定约束的问题获取最佳解决方案。在线性编程中，我们将我们的实际问题化为数学模型。它涉及一个客观函数，线性不等式，受约束。
上面 6 点的线性表示是否代表真实世界？是和否。这是一个过于简单化，因为真正的路线不会是一条直线。它很可能有多圈， U转弯，信号和交通堵塞。但是，通过一个简单的假设，我们大大减少了问题的复杂性，并正在创建一个解决方案，应该在大多数情况下工作。
制定一个问题 – 让我们制造一些巧克力
示例：以一家只生产两种巧克力的巧克力制造公司考虑吧—— A和B 。这两种巧克力只需要牛奶和巧克力。要制造每个 A 和 B 单元，需要以下数量：

A 的每个单位需要 1 个单位的牛奶和 3 个单位的巧克力
B 的每个单位需要 1 个单位的牛奶和 2 个单位的巧克力

公司厨房共有5个单位的牛奶和12个单位的巧克力。每次出售时，公司都盈利。

每售出单位 A 6Rs
每售出 B 单位 5Rs 。

现在，公司希望实现利润最大化。它应该分别生产多少个 A 和 B 单位？
解决方案：我要做的第一件事是用表格形式表示问题，以便更好地理解。
牛奶崔克单位利润A136B125总512
让 A 生产的单位总数为 = X
让 B 生产的单位总数 = Y
现在，总利润由 Z 表示
公司利润总额按生产单位总数乘以单位利润 6 Rs 和 Rs 5 。
利润：最大 Z = 6 倍~5 年
这意味着我们必须最大化 Z。
公司将尝试生产尽可能多的 A 和 B 单位，以最大限度地提高利润。但资源牛奶和巧克力是有限的可用量。
根据上表， A 和 B 的每个单位需要 1 单位牛奶。牛奶的总量为5个单位。为了用数学来表示这一点，
X=Y = 5
此外， A 和 B 的每个单位分别需要 3 个单位和 2 个单位的 Choco 。可用的巧克力总量为 12 个单位。为了用数学来表示这一点，
3X×2Y = 12
此外， A 单位的值只能是整数。
因此，我们还有两个约束， X = 0 和 Y = 0
公司要想实现利润最大化，必须满足上述不平等。
这称为将一个真实世界的问题形成数学模型。
线性编程中使用的常用术语
让我们使用上述示例定义线性编程中使用的一些术语。

决策变量：决策变量是决定我的输出的变量。它们代表了我的最终解决方案。要解决任何问题，我们首先需要确定决策变量。对于上述示例，分别由 X 和 Y 表示的 A 和 B 的单位总数是我的决策变量。
目标函数：它被定义为决策的目标。在上面的示例中，公司希望增加 Z 表示的总利润。所以，利润是我的客观功能。
约束：约束是决策变量的限制或限制。它们通常限制决策变量的值。在上面的示例中，对资源可用性的限制是我的限制。
非负性限制：对于所有线性程序，决策变量应始终使用非负值。这意味着决策变量的值应大于或等于 0 。

制定线性编程问题的过程
让我们来一般地查看定义线性编程问题的步骤：

确定决策变量
编写目标函数
提及约束
明确说明非负性限制

要使问题成为线性编程问题，决策变量、目标函数和约束必须都是线性函数。
如果满足这三个条件，它被称为线性编程问题。
2. 用图形方法求解线性程序
线性程序可以通过多种方法解决。在本节中，我们将介绍求解线性程序的图形方法。此方法用于求解双变量线性程序。如果只有两个决策变量，则应使用图形方法找到最佳解决方案。
图形方法涉及根据约束制定一组线性不等式。然后在 X-Y 平面上绘制不等式。一旦我们绘制了图形上的所有不等式，相交区域将给我们一个可行的区域。可行区域说明了我们的模型可以采取的所有值。它还为我们提供了最佳解决方案。
让我们通过一个示例来理解这一点。
示例：一位农民最近获得了一块110公顷的土地。他决定在那块土地上种植小麦和大麦。由于太阳的质量和该地区的优良气候，小麦和大麦的整个生产可以出售。他想知道如何种植每一个品种在110公顷，考虑到成本，净利润和劳动力要求，根据以下数据显示：
品种成本（价格/价格）净利润（价格/价格）人日/Hec小麦1005010大麦20012030
农民的预算为10 ， 000美元，在规划期间提供1 ， 200人日。找到最佳解决方案和最佳价值。
解决方案：为了解决这个问题，首先我们制定我们的线性程序。
线性问题的公式
第 1 步：确定决策变量
种植小麦的总面积 = X（公顷）
种植大麦的总面积 = Y（公顷）
X 和 Y 是我的决策变量。
第 2 步：编写目标函数
由于生产从整个土地可以在市场上出售。农夫希望最大限度地提高他总生产的利润。我们获得小麦和大麦的净利润。农民每公顷小麦的净利润为50美元，大麦的净利润为120美元。
我们的目标函数（由 Z 给出）是，最大 Z = 50 倍 = 120Y
第 3 步：编写约束
1. 鉴于农民的总预算为10 000美元。每公顷小麦和大麦的生产成本也由我们支付。我们对农民花费的总成本有上限。因此，我们的方程变为：
100X = 200Y = 10 ， 000
2. 下一个限制是规划视界人日总数上限。可用人日总数为 1200 天。根据表，我们得到小麦和大麦每公顷的人日。
10X × 30Y × 1200
3. 第三个限制是种植园的总面积。总可用面积为110公顷。所以方程变成了，
X = Y = 110
第4步：非负性限制
X 和 Y 的值将大于或等于 0 。这不言而喻。
X = 0 ，Y = 0
我们已经制定了线性程序。是时候解决它了。
通过图形方法解决 LP
因为我们知道 X ，Y = 0。我们将只考虑第一个象限。
要为上述方程绘制图形，首先我将简化所有方程。
100X = 200Y = 10 ， 000 可以简化为 X = 2Y = 100 除以 100 。
10X = 30Y = 1200 可以简化为 X = 3Y = 120 除以 10 。
第三个方程以简化形式， X = Y = 110 。
在第一个象限中绘制图形上的前 2 行（如下所示）
最佳可行的解决方案在预算和人日约束活跃的交叉点实现。这意味着方程 X = 2Y = 100 和 X = 3Y = 120 相交的点为我们提供了最佳解。
提供最佳解决方案的 X 和 Y 的值为（60 ， 20）。
为了利润最大化，农民应分别生产60公顷和20公顷土地的小麦和大麦。
公司获得的最大利润是：
最大 Z = 50 * （60） = 120 * （20）
￥ $5400

注：这里教授的所有课程也以课程形式教授，在这个免费课程 -
3. 使用R求解线性程序
R 是一种开源工具，在数据科学家中非常受欢迎，用于执行必要的数据科学任务。执行线性编程非常简单，我们可以在很少的步骤中实现最佳解决方案。来吧，让我们学习。
示例：玩具制造组织生产两种类型的玩具 A 和 B 。这两种玩具的售价分别为25欧元和20欧元。有2000个资源单位，每天从玩具 A 需要 20 个单位，而玩具 B 需要 12 个单位。这两个玩具都需要5分钟的生产时间。总工作时间为每天9小时。每个管道的制造数量应该是多少，以最大化利润？
这里：
目标函数为：Max.Z=25x=20y

其中 x 是管道 A 的单位
y 是管道 B 的单位
约束：20x=12y<=2000

5x=5y<=540
现在让我们看看代码部分：
安装. 包（[lpsolve
)库（lpsolve)#设置决策变量的系数objective.in=c （25 ， 20)#约束矩阵const.mat=矩阵（c）20 ， 12 ， 5 ， 5）， nrow = 2 ， byrow = T)#定义约束const_time540 °分钟const_res=2000#用于约束的 RHSconst. rhs_c（const_res ， const_time)#约束方向const.dir=c（"<=" ， "<=")#寻找最佳解决方案选择\\lp （方向= "最大" ， objective.in ，const. mat ， const. dir ， const. rhs )摘要（选择)#x 和 y 的客观值选择$解决方案#最佳点目标函数的值选择$objval
lpp.R由Github ?托管
输出
summary(opt)Length Class Mode direction 1 -none- numeric x.count 1 -none- numeric objective 2 -none- numeric const.count 1 -none- numeric constraints 8 -none- numeric int.count 1 -none- numeric int.vec 1 -none- numeric bin.count 1 -none- numeric binary.vec 1 -none- numeric num.bin.solns 1 -none- numeric objval 1 -none- numeric solution 2 -none- numeric presolve 1 -none- numeric compute.sens 1 -none- numeric sens.coef.from 1 -none- numeric sens.coef.to 1 -none- numeric duals 1 -none- numeric duals.from 1 -none- numeric duals.to 1 -none- numeric scale 1 -none- numeric use.dense 1 -none- numeric dense.col 1 -none- numeric dense.val 1 -none- numeric dense.const.nrow 1 -none- numeric dense.ctr 1 -none- numeric use.rw 1 -none- numeric tmp 1 -none- characterstatus 1 -none- numeric > opt$solution[1
88 20> opt$objval[1
2600
因此，从产量上，我们看到组织应生产88台玩具 A 和 20 台玩具 B ，组织的最大利润为 2600 Rs 。
4. 使用开解器求解线性程序
实际上，线性程序可以包含 30 到 1000 个变量，并且以图形方式或代数方式求解它几乎是不可能的。公司通常使用 OpenSolver 来解决这些实际问题。在这里，我要带你通过步骤来解决一个线性程序使用开放解。
OpenSolver 是微软 Excel 的开源线性和优化器。它是内置 Excel 解算器的高级版本。您可以在此处下载并按照安装。
我想让你获得使用 OpenSolver 的动手知识。因此，为了清楚地理解，我将用一个例子来解释它。
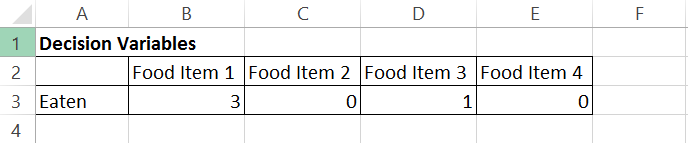
示例：下面有一个饮食图，给我卡路里，蛋白质，碳水化合物和脂肪含量的4个食物。萨拉想要一个最低成本的饮食。饮食图表如下：
食品项目1食品项目2食品项目3食品项目 4卡路里400 200 150 500普罗蒂安（克）3 2 0 0碳水化合物（克）2 2 4 4脂肪（克）2 4 1 5成本$0.50$0.20$0.30$0.80
该图表给出了每个食品的营养成分和单位成本。饮食必须计划的方式，它应该包含至少500卡路里， 6克蛋白质， 10克碳水化合物和8克脂肪。
解决方案：首先，我要在电子表格中制定我的线性程序。

第 1 步：确定决策变量。在这里，我的决策变量是食品。添加标头。出于试用目的，我们输入任意值。比来说， Sara 消耗 3 个单位的食品项目 1 ，0 单位的食品项目 2 ，1 单位的食物项目 3 和 0 单位的食物项目 4.这些称为可变单元格。

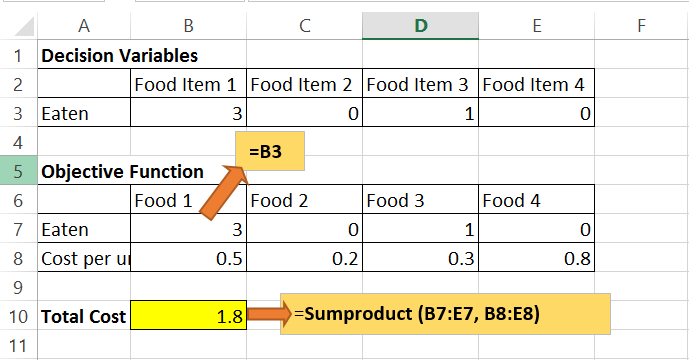
第 2 步：现在，我们将编写我们的客观函数。为了使饮食达到最佳状态，我们必须有最低的成本以及所需的卡路里、蛋白质、碳水化合物和脂肪。

在单元格 B7：E7 中，我们引用单位数。在单元格 B8：E8 中，我们计算每个食品的单位成本。
在细胞B10中，我们想要饮食的总成本。总成本由已吃单位数和单位成本的总和给出。总和产品由 + B7*B8+C7*C8+D7*D8+E7*E8 提供。让我们在电子表格中查看。

第 3 步：现在，我们将输入约束。列 F 包含卡路里、蛋白质、碳水化合物和脂肪。总产中卡路里摄入的总数，即所吃的食物数量和每个食物消耗的卡路里。对于单元格 F13= Sumprodcut（$B$7：$F$7 ，B13：F13）。对其他人来说也差不多。 G 列给出了不平等，因为问题要求卡路里、蛋白质、碳水化合物和脂肪分别至少为 500、6、10 和 8 。列 H 提供所需的营养成分。

第4步：现在，我们将线性程序输入解算器。现在，一旦您安装了 OpenSolver 。当您单击"数据"选项卡时，在右侧将看到"模型" 。单击模型，然后一个输入值。首先，我们将在目标单元格中输入$B函数，即10 。选择最小化，因为我们想尽量减少饮食成本。

第 5 步：现在输入变量单元格中的决策变量。

步骤 6：现在，我们将添加约束。第一个约束是 F13 = H13 。一个添加所有约束。

第 7 步：现在，您必须输入一个重要的约束。非消极限制。所有决策变量将大于 0 。

步骤 8：现在，单击"保存模型"完成建模过程。保存模型后，它将看起来像这样。

步骤 9：保存模型后，单击"数据"选项卡，然后单击求解。最佳解和值显示在相应的单元格中。最佳最低成本为0.90美元。 Sara 应以最低成本消耗 3 个单位的食物项目 2 和 1 单位的食物项目 3 所需的营养成分。这解决了我们的线性程序。

5. 简单方法
Simplex 方法是线性编程最强大、最流行的方法之一。简单方法是一个迭代过程，用于获得最可行的解决方案。在此方法中，我们不断变换基本变量的值，以获得目标函数的最大值。

如果线性编程函数寻求最大化目标函数，它将是标准形式的。受限制，. . . . . .
. . . . . .

在哪里和。添加松弛变量后，相应的约束方程系统是，

. . . .

在哪里，
变量， ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...它们是非负数，用于从等式中删除不等式。以上解释对简单方法进行了理论解释。现在，我将解释如何在现实生活中使用Excel使用简单方法。
示例：公司的广告选择包括电视、报纸和广播广告。每家媒体及其受众覆盖的成本如下。
电视报纸无线电每个广告的成本（美元）2000 600 300每个广告的受众1000004000018000
当地报纸将单一公司的广告数量限制在10个。此外，为了平衡三类媒体之间的广告，电台广告总数的一半不应超过一半。至少10%应该在电视上出现。每周广告预算为18 ， 200美元。三种媒体中每个媒体应运行多少个广告，以最大限度地提高总受众？
解决方案：首先我要制定我的问题，以便有一个清晰的理解。
第 1 步：确定决策变量

让，分别表示电视、报纸和广播的广告总数。第 2 步：目标函数
公司的目标是最大限度地吸引受众。目标函数由以下因素提供：

第 3 步：记下约束
现在，我将一个一个地提到每个约束。
显然，我们有预算限制。可分配的预算总额为18 200美元。每则电视、报纸及电台广告的个别费用分别是2000元、600元及300元。这可以通过方程来表示，

对于报纸广告，广告数量上限为10 。我的第一个限制是下一个限制是电视上的广告数量。该公司希望至少10%的广告在电视上播放。因此，它可以表示为：

最后一个约束是收音机上的广告数不能超过播发总数的一半。它可以表示为

现在，我已经提出了我的线性编程问题。我们使用简单方法来解决这个问题。我将带你一个一个地通过简单的方法。
重申所有限制如下。我简化了最后两个方程，以标准形式将它们引入。

我们总共有4个方程。为了平衡每个方程，我引入了 4 个松弛变量和。因此，我们的方程如下所示：

我希望现在你能理解整个广告问题。以上所有方程都只是为了你更好的理解。现在，如果求解这些方程，将得到 X1= 4、X2= 10 和 X3= 14 的值。
在解决目标函数时，您将获得每周最大观众人数为 1 ， 052 ， 000 。您可以按照此处求解方程。要解决 Excel 中的线性程序，请按照本教程。
6. 西北角法与成本法
6.1 西北角方法
西北角法是线性编程中用于运输问题的一种特殊类型方法。它用于计算将商品从一个地方运送到另一个地方的可行解决方案。每当你得到一个现实世界的问题，这涉及到来自不同来源的一个来源的供求关系。数据模型包括以下内容：

给出每个来源的供求水平
商品从每个来源到每个目的地的单位运输

该模型假定只有一种商品。需求可能来自不同的来源。目标是以最低运输成本满足总需求。该模型基于总需求等于总供给的假设，即模型是平衡的。让我们通过一个示例来理解这一点。
示例：考虑有 3 个筒仓，需要满足 4 个磨厂的需求。（筒仓是用于储存谷物的农场的储存区，磨坊是谷物研磨厂）。

解决方案：让我们了解上表所解释的。
从思洛 i 到 Mill j 的运输成本由每个单元中与每个思洛 1 的供应量和每个磨坊的需求对应的成本给出。例如，从思洛 1 到磨坊 1 的运输成本为 10 美元，从思洛 3 到磨坊 5 的运输成本为 18 美元。它还被赋予了磨坊和筒仓的总需求和供应。目标是找到最低的运输成本，使所有工厂的需求得到满足。
正如名称建议西北角方法是一种从左上角单元格开始分配单位的方法。对磨坊 1 的需求为 5 ，思洛 1 的总供应量为 15 。因此， 5 个单位可以分配给 Mill1 ，每单位成本为 10 美元。满足对 Mill1 的需求。然后我们移动到磨坊 2 的左上角单元格。对 Mill 2 的需求为 15 个单位，它可以从 Silo 1 获得 10 个单位，每单位成本为 2 美元，从 Silo 2 获得 5 个单位，每单位成本为 7 美元。然后我们移动到磨坊3 ，西北单元是S2M3 。对磨坊 3 的需求为 15 个单位，可以从思洛 2 获得，每单位成本为 9 美元。进入最后一个磨坊，磨坊4有15个单位的需求。它将从思洛2获得5个单位，每单位成本20美元，从思洛3获得10个单位，每单位18美元。
运输总费用为 = 5*10+（2*10+7*5）=9*15=（20*5=18*10） = $520

6.2 成本最小方法
成本法是计算线性编程问题最可行解决方案的另一种方法。此方法比西北角方法获得更准确的结果。它用于运输和制造问题。为了简单，我解释上述交通问题。

根据成本最少的方法，从包含运输单位成本最少的单元开始。因此，对于上述问题，我以每单位4美元的价格从Silo 3供应5个单位。满足对 Mill1 的需求。对于磨坊 2 ，我们从思洛 1 号供应 15 个单位，单位成本为 2 美元。然后，对于磨坊 3 ，我们从思洛 2 提供 15 个单位，每单位成本为 9 美元。然后，对于 Mill 4 ，我们以每单位成本 20 美元从 Silo 2 供应 10 个单位，从 Silo 3 提供 5 个单位，每单位 18 美元。运输费用共计475美元。
那么，上述方法说明，我们可以用最好的方法进一步优化成本。让我们使用 Excel 解算器来检查这一点。解算器是 Microsoft Excel 中内置的加载项。它是 Excel 中可用的外接程序插件。转到文件>选项->外接程序->选择解算器->单击管理->选择求解器->单击确定。您的解算器现在以 Excel 添加。您可以在"数据"选项卡下检查它。
我要做的第一件事是以 Excel 输入我的数据。在 Excel 中输入数据后，我计算了 C3：F3 的总数。对其他人来说也差不多。这样做是为了从思洛 1 和其他人那里获得总需求。

在此之后，我要把我的模型分成两个。第一个表给了我提供的单位，第二个表给了我单位成本。

Now I am calculating my total cost which will be given by Sumproduct of unit cost and units supplied.

Now I am gonna use Solver to compute my model. Similar to the above method. Add the objective function variable cells constraints.

Now your model is ready to be solved. Click on solve and you will get your optimal cost. The minimum transportation cost is $435.

7. 线性编程的应用
线性编程和优化用于各种行业。制造业和服务业经常使用线性编程。在本节中，我们将介绍线性编程的各种应用。

制造业使用线性编程来分析其供应链运营。他们的动机是以最小的运行成本最大限度地提高效率。根据线性编程模型的建议，制造商可以重新配置其存储布局、调整其员工队伍并减少瓶颈。这里是一个小仓库案例研究的Cequent的一家美国公司，观看，以更清楚地了解。
线性编程也用于有组织的零售货架空间优化。由于市场上的产品数量突飞猛进，因此了解客户想要什么非常重要。优化在沃尔玛、超城、信实、大集市等商店中积极使用。商店里的产品是战略性地放置的，牢记顾客的购物模式。目标是使客户能够轻松找到并选择合适的产品。这受到限制，如有限的货架空间，各种产品等。
优化也用于优化传递路由。这是流行的旅游推销员问题的延伸。服务行业使用优化为前往多个城市的多个销售人员寻找最佳路线。借助聚类和贪婪算法，交付路线由联邦快递、亚马逊等公司决定。目标是最大限度地降低操作成本和时间。
优化也用于机器学习。监督学习是线性编程的基本知识。系统经过训练，以适应来自标记输入数据的函数的数学模型，该输入数据可以从未知测试数据预测值。

嗯，线性编程的应用不会在这里结束。线性编程在现实世界中应用了更多，如股东、体育、股票市场等。继续探索。
结束备注
我希望你喜欢读这篇文章。我试图解释线性编程下的所有基本概念。如果您有任何疑问或疑问，请随时在评论部分发布。为了便于理解，我们将这篇长文章分解为较短的课程格式 -
我已经用一个真实的例子解释了每个概念。我希望你尝试他们在你的结束，并得到实践经验。让我知道你怎么想！

【编程|数据科学家线性编程入门指南】作者：Vidhya