江苏龙网

  1. 首页 > 资讯 > 科技 > >

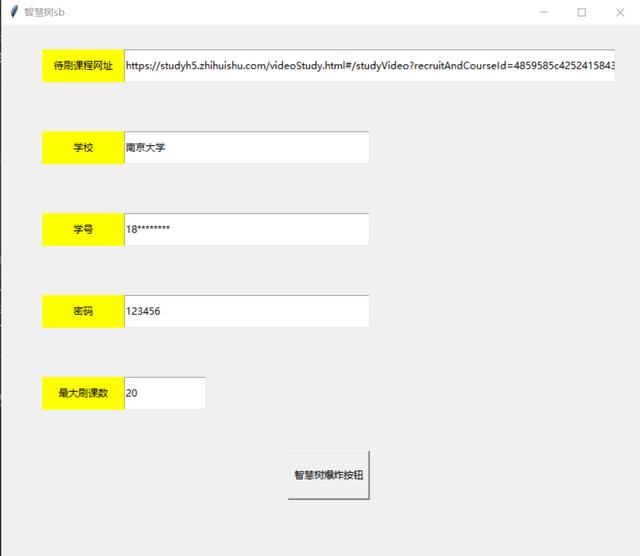
智能小屋MUKK|这是计算机AI自我学习的最大障碍吗？


计算机自我学习？ 是的而且这已经在我们身边发生了 。 只是可能您没有发现 ， 或者没有注意到而已 。 今天来说一下关于计算机学习的问题 ， 或者障碍 。
问题与机器学习有关 ， 某些计算机用来“学习”如何完成特定任务的人工智能模型的类型 。 不过计算机学习并不是那么顺利 ， 这个可能是一个数学问题 。 数学家发现了他们无法解决的问题 ， 阻碍了计算机的学习 。 不是说他们不够聪明 ， 解决不了 ， 而是根本没有答案 。

智能小屋MUKK|这是计算机AI自我学习的最大障碍吗？
本文插图

AI计算机学习
当无人驾驶汽车在繁忙的十字路口导航时 ， 这就是机器学习的作用 。 神经科学家使用机器学习来“阅读”某人的想法 。 关于机器学习的事情是它基于数学 。 数学家可以在理论水平上对其进行研究和理解 。 他们可以写出关于机器学习如何工作的证明 ， 这些证明是绝对的 ， 并且是正确的 。 基于此 ， 一组数学家设计了一个机器学习问题 ， 称为“估计最大值”或“ EMX” 。
智能小屋MUKK|这是计算机AI自我学习的最大障碍吗？
本文插图

AI计算机学习
要了解EMX的工作原理 ， 请想象一下：您想在网站上放置广告 ， 并最大程度地将这些广告展示给目标受众 。 您有向体育迷 ， 爱猫者 ， 汽车迷和运动爱好者等投放广告 。 但您事先并不知道谁将访问该网站 。 您如何挑选广告来最大化您定位的观众数量？EMX只能用少量有关谁访问该网站的数据来找出答案 。 然后研究人员提出了一个问题：EMX何时可以解决问题？研究人员表明EMX与连续性假设密不可分 。

智能小屋MUKK|这是计算机AI自我学习的最大障碍吗？
本文插图

AI计算机学习
事实证明 ， 只有在连续性假设成立的情况下 ， EMX才能解决问题 。 但是 ， 如果这不是真的 ， 那么EMX就不能 。 这意味着“ EMX能学会解决这个问题吗？”这个问题的答案与连续性假设本身一样令人难以回答 。
连续性假说是这样的：数学家已经知道存在不同大小的无穷大 。 例如 ， 有无数个整数（例如1、2、3、4、5等） 。 并且有无数个实数（包括数字1、2、3等 ， 但也包括数字1.8、5,222.7和pi） 。 但是 ， 即使有无限多的整数和无限多的实数 ， 显然实数比整数还多 ， 因为有小数点 。 这就提出了一个问题 ， 是否有任何无穷大于整数集而小于实数集？连续体假设说：不 ， 没有 。

智能小屋MUKK|这是计算机AI自我学习的最大障碍吗？
本文插图

AI计算机学习
这表明 ， 不可能证明连续性假设是正确的 ， 但也不可能证明它是错误的 。 “连续性假设是真的吗？” 是一个没有答案的问题 。
【智能小屋MUKK|这是计算机AI自我学习的最大障碍吗？】好消息是 ， 对于大多数数学来说 ， 解决连续性假设的问题并不是很重要 。 由此可知 ， 这个永久性的谜团可能不会对机器学习造成重大障碍 。 所以我们的计算机学习会有很大的障碍但是最终都能够完成它的学习 。


    推荐阅读


    上一篇：科技犬|双屏笔电成未来发展趋势 华硕灵耀X2 Duo打造绝佳生产力工具

    下一篇：荣县|发展电商促进创业 荣县首个电商众创孵化服务中心挂牌成立