咋学立体几何?
谢邀!很多同学觉得立体几何很难,看到题目往往无从下手。而很多老师也宣称要学好立体几何需要具备所谓的“良好的空间想象能力”。看起来似乎很有道理,其实经不起推敲。在我看来,这种归因,说难听些,很有误人子弟之嫌。什么叫“良好的空间想象能力”,这本就是一个模糊的概念。用一个未界定清楚的概念去解释一种现象是极度不负责任的,这导致的后果就是很多学生潜意识会做出这样的推理:1) 我的立体几何学不好 -\u0026gt;2) 因为我没有良好的空间想象能力 -\u0026gt;3) 良好的空间想象能力应该是天生的 -\u0026gt;4) 因此我立体几何学不好是天生比别人在这方面“笨”-\u0026gt;5) 因此我再怎么努力也是徒劳的。而很多老师地教不得法,让那些努力学习了的孩子仍旧取不得进步,于是,他们就更加相信上面的推理了,最终成为恶性循环。在这里我想告诉这些努力了但没有收到效果的同学们一个好消息:不是你没有天分,而是你一直被错误地教导,你自己也在错误地归因,仅此而已。事实上,你只要学好本质教育的三招中的第3招-盯住目标和第1招-翻译就可以解决高考难度的所有立体集合题目了。我用两道高考难度的例题带领大家学习下这两招,并说明如何灵活地运用他们。

我希望同学们在看我的分析前,先自己试着解答一下,看看你能否做出来,如果做出来了,看看能否一题多解。)在我们开始分析之前,我们先来了解下本质教育数学第3招 – 盯住目标。事实上,任何解题的过程都是在已知(前提)和未知(结论)之间构建一个桥梁。我们把未知或者题目要证明的结论统称为目标(purpose)。解题的高手很清楚“有的放矢”这几个字, 我们往往不仅仅从已知出发正向构建桥梁,而是反过来从目标出发,反向构建桥梁:

在这个不断更新目标的过程中,我们反复问自己:盯住目标 – 你能联想相关的定理,方法,定义吗?你能试着把目标和已知,前提结合吗? 这就是不断地调用学习过的知识的过程。这第三招这样看起来很抽象,我们通过例1来说明就会清楚多了:例1的第一问的目标就是求证EF
面GMC,这是一个求证线面垂直的问题。我们利用第三招,从目标出发,问自己:盯住目标 – 你能联想相关的定理,方法,定义吗?事实上,整个立体几何第一章空间的直线和平面的绝大多数定理可以用下图来总结:
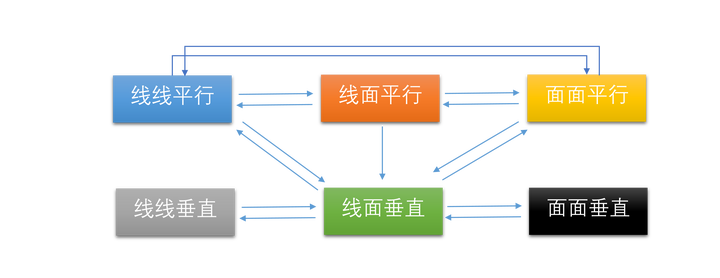
换句话说,要证明线面垂直,我们应该根据此图联想出以下几个定理:(1)线线垂直-\u0026gt;线面垂直:若直线若直线
与平面
内的两条相交直线垂直,那么
(2)线线平行-\u0026gt;线面垂直:若直线
与平面
垂直,直线all
a
(3)面面垂直-\u0026gt;线面垂直:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂 直于另一个平面而联想出这3个定理,其实也对应着3种不同的证明方法:
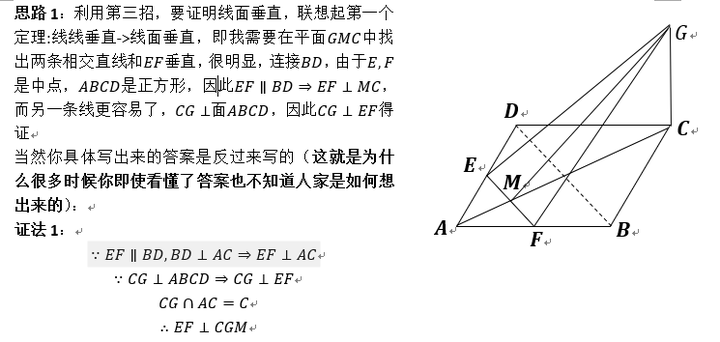
【咋学立体几何?】 


(还有别的解法吗?你能够联想不同的定理吗,你能够用另一种方法“翻译”这个问题吗?提示:空间向量)回顾我的解题思路,用到了所谓的“空间想象力”了吗?完全没有!




通过例2,大家应该知道这些辅助线不是胡乱猜出来的,而是根据我们的第三招,有的放矢的找出来的!联想不同的定理,我们有不同的证明方法!我们用到了所谓的“空间想象力”了吗?还是没有。这两题就是高考所能考察立体几何的难度,我们不仅能做,还能够用多种方法求解,这就是我们本质教育三招的妙处,而这3招正是数学哲学的一部分,是一流数学家解决问题的思维方式。学习这三招就和游泳类似,你在岸上看我如何游泳是永远学不会如何游泳的,你必须下水,哪怕呛一两口水也好,这样才能知行合一。
同时推荐我的另外两篇文章:
Zeyu(李泽宇):为什么我的数学成绩无法提高
Zeyu(李泽宇):如何学好高中数学 ——我的经历与启示
■网友的回复
数学狗,兼职家教,谈一下对这个问题的几个不同方法。1.有部分朋友会有着极强的空间想象能力,当然这种能力不一定十分显著,但譬如你识路能力很强,去过一次的地方都能记住路,看地图不用翻来倒去找北,那么可以考虑一下这种办法:我谨称为,冥想法。适度开发一下自己的空间想象能力,拿到一个题目,不要直接按照老师可能教的,谁和谁平行,谁谁垂直,夹角多少啥的来分析题目。特别在练习的时候,直接试图在脑海里勾勒出这个图形,甚至可以闭上眼睛。当然,在最初会比较难做到,可以在想不出来以后画图辅助,当然在你“冥想”技能娴熟以后,也会同时加强你的画图技能。说白了,立体几何和平面几何都是几何的范畴,而且一般反而出不了特别困难,主要是如何利用已知条件,难点就在于已知条件甚至记不住,遇到问题都想不起来有这个条件(这里一般指和位置关系有关的条件),如果能在脑海里勾勒出这个图形,大部分题目迎刃而解。2.如果朋友是路痴,正方体六个面想不出来对面是什么样,最好就不要尝试“冥想”法了。这个时候有另外的一种方式,脱胎于空间直角坐标系。把你题目里的几何图形,放到一个大长方体内,用一个直角顶点作为长方体的一个顶点,剩下的角尽量落在这个长方体内的边,角上。这个几何图形的性质就会变得特别清晰,有兴趣的同学可以试一下。
■网友的回复
我也是准高二,但立体几何这一块已经学完了。我觉得你可以多画图。我们老师补课时所有题目都让我们自己抄下来,把图自己画下来,画一遍图你题目就理解了一大半。我学过五年素描,对立体几何很有感触和体会,毕竟素描一上来就画这种东西,很培养空间立体思维。但是你突击素描之类的不太可能,所以你可以买本《小题狂做》之类的,只要有立体几何的教辅都行,买这类书来做做,多刷题真的有好处。我十天连学习带刷题大约做掉了70道题(我刷的算少的),现在感觉真的是熟能生巧,大部分稍微想想就会了。可是我还是比不上高三的姐姐,因为她刷过的比我多的多。建议画图用不同颜色的笔,五颜六色大胆画!看得见的用实线,看不见的用虚线!然后做题前先把线面平行垂直的定理、性质定理还有面面的定理性质定理搞清楚,理解很重要!不然干嘛说理解万岁嘛!证明线面垂直有5步,2实3虚有没有都写?证明平行四边形之类的有没有跳步骤?证明过程会不会太牵强或者太繁琐?这些都要考虑。建议做好让老师看看,毕竟格式真的很重要,少写步骤扣分真的很不好。初期好的做题习惯一定要养成哦!
推荐阅读
- 哪些行为不会使女性显得俗不可耐
- 大多数大学生真的丧失了生活的热情吗
- 抑郁焦虑是不是伴有持续失眠噩梦症状
- 万能的知友,谁知道哪有这种。外形类似白炽灯的灯卖
- 食物能润肺有科学依据么
- 到底啥才算是抱怨
- 职场上一直有人针对咋办
- 输血所用的血液中是不是含有肝素 枸橼酸钠等抗凝剂
- 怎样选择美式沙发搭配
- 那些因为抑郁症而休学/辞职的人,现在都咋样了



















