江苏龙网

  1. 首页 > 人文 > >

#三维空间#三维空间也许是最后一个维度


#三维空间#三维空间也许是最后一个维度
文章图片
#三维空间#三维空间也许是最后一个维度
文章图片
#三维空间#三维空间也许是最后一个维度
文章图片
#三维空间#三维空间也许是最后一个维度
为什么三维空间那么特别？
我们人类能直接感觉到的尺度大小是以1米为单位的 ， 在这个尺度上 ， 空间显然是三维的 。 在我们人类的世界里 ， 所有房子的墙角都有三个方向 ， 也就是要有三个平面才可以决定一个墙角 ， 所以从直观上看来 ， 我们的空间是三维的 。
阿拉伯数字“3”被认为是符合中国的道家文化中所说的“一生二 ， 二生三 ， 三生万物”的哲学思想 。 在作者看来 ， “3”这个数字在数学、物理领域也非常特别 ， 比如空间是三维的 ， 组成原子核的夸克有三种基本颜色 ， 周期三会导致混沌 ， 三维空间内会出现蝴蝶效应等等 。 如果你喜欢勾股定理并且喜欢把它推广到立方和的形式而跌到在地 ， 你仰头看见了费马大定理 ， 这个时候 ， 你一定会觉得平方是那么特殊 ， 而空间是三维的 ， 这也许是一个宿命 。
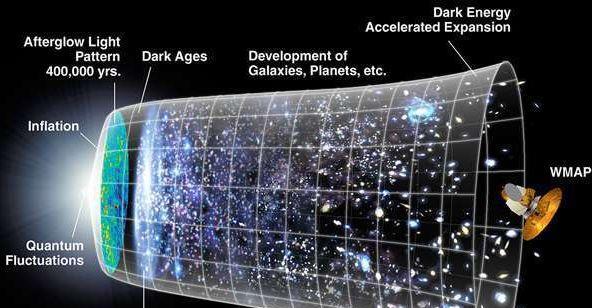
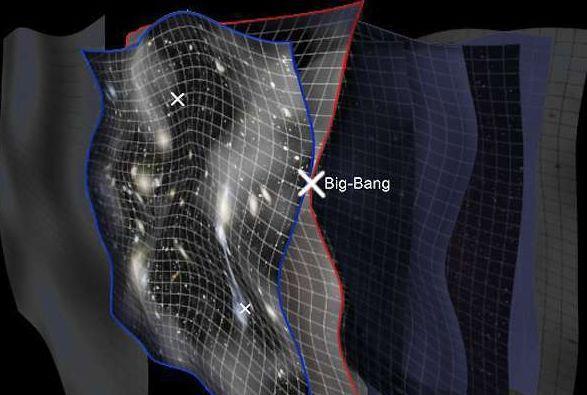
根据爱因斯坦的广义相对论 ， 时空的结构由万有引力决定 ， 那么我们先从万有引力上来寻找答案 。 牛顿的万有引力与距离的平方成反比 ， 这就是空间是三维的直接结果 ， 如果空间是二维的 ， 那么牛顿万有引力与距离的关系就会变成对数关系 。 维度(dimension)是一个数学概念 ， 豪斯多夫有一个分形维度的定义：存在一个单位几何体 ， 如果把线尺度放大a倍 ， 我们得到b个单位几何体 。 那么b等于a的n次方 ， 这样 ， n等于lnb/lna 。 这就是维度 。 用这个定义 ， 你可以得到一些分数维度 ， 比如对英国的海岸线 ， 你可以得到一个分数维度 ， 这背后的数学被称为分形几何 。
如果你时常观察星空 ， 一定会觉得星星在天幕上是稀稀拉拉的 。 天幕或者说天球是一个二维球面 。 星星的分布具有一个分形的维度 ， 这个维度大概是1.2 。 因为这个分布的维度小于2 ， 因此在我们才看来 ， 星星没有布满整个天球 。 我们这里说的是星星在天球上的分布是一个角分布 。 对于时空来说 ， 维度也是与之类似的一个概念 ， 但这是一个约定俗成的概念 。 一般来说 ， 人们总是设想时空的维度是整数 。 关键是 ， 这个整数是多少？
人择原理可以说明 ， 假如空间维度大于3 ， 那么 ， 地球绕太阳运动和电子绕原子核的运动就不是稳定的 ， 人类就不能出现 。 人类不出现 ， 就没有人来提出这个问题 ， 既然有人提出这个问题 ， 就可以说明时空是四维的(也就是空间是三维的) 。 人择原理非常特殊 ， 有点像一个哲学原理 ， 但它可以解释物理问题 ， 所以对于这一原理在物理学中的地位问题 ， 作者与一个师兄(张宏宝)在面见霍金的时候请教过霍金 ， 霍金只给我们解释了什么是人择原理 ， 对它的意义也三缄其口 。
电子绕原子核运动
曾经有人研究过高维空间吗？
是的 ， 曾经有人研究过 。 是哥尼斯堡 ， 于1919年 。 34岁的数学系教授西奥多·卡鲁扎（Theodor Franz Eduard Kaluza）从雾霾中醒来 ， 看了一下阳台上的那根晾衣服的细绳子 ， 似乎见不到了 。 但老婆刚洗好的衣服还挂在上面 ， 正在朝地上滴答滴答地流水 ， 卡鲁扎教授知道 ， 那绳子想必是一定还在的 。
卡鲁扎教授一般睡到中午起床 ， 直接吃中饭 ， 他喜欢在凌晨工作 ， 凌晨的时候他的脑子最清晰 ， 最适合做数学研究——当然他自信自己的脑子还是很有用的 ， 他曾经看了一本关于游泳的书 ， 等把这本书读熟以后 ， 他一下水 ， 就按照书上讲的动作要领做动作 ， 就马上学会了游泳——所以他一直相信理论的力量 。 那时候 ， 江湖上在闹一个理论革命 ， 那就是爱因斯坦的广义相对论被爱丁顿领导的实验所证明 ， 这时闹得学术圈分外亢奋 ， 卡鲁扎教授也不由得去读了读爱因斯坦的广义相对论的数学方程 ， 之后发现这玩意很神奇 ， 但是爱因斯坦是在一个四维时空上建立的方程 。 这里面有一个漏洞 ， 卡鲁扎心想：我可以把方程放在五维时空里来解 ， 这只不过是一个数学游戏而已 。


推荐阅读


上一篇：「智能手表」支持eSIM的4款智能手表：颜值最高的售价竟不超1500元

下一篇：『外星人』揭秘：外星人一直在插手地球上的战争