有哪些一眼看上去并不震撼的问题,实际上很难解答或者根本无法解决
自行车为什么稳定?
水平的喷水如何在低速下附着竖直的管子?
随即写一段代码,它能成功运行的概率是多少?
是否任意一个大偶数都能表示为两个素数之和?
这些都是世界未解之题。
■网友的回复

哥德巴赫1742年给欧拉的信中哥德巴赫提出了以下猜想:任一大于2的整数都可写成三个质数之和。
但是哥德巴赫自己无法证明它,于是就写信请教赫赫有名的大数学家欧拉帮忙证明,但是一直到死,欧拉也无法证明。
因现今数学界已经不使用“1也是素数”这个约定,原初猜想的现代陈述为:任一大于5的整数都可写成三个质数之和。(n\u0026gt;5:当n为偶数,n=2+(n-2),n-2也是偶数,可以分解为两个质数的和;当n为奇数,n=3+(n-3),n-3也是偶数,可以分解为两个质数的和)欧拉在回信中也提出另一等价版本,即任一大于2的偶数都可写成两个质数之和。
今日常见的猜想陈述为欧拉的版本,即任一大于2的偶数都可写成两个素数之和,亦称为“强哥德巴赫猜想”或“关于偶数的哥德巴赫猜想”。
从关于偶数的哥德巴赫猜想,可推出:任一大于7的奇数都可写成三个质数之和的猜想。后者称为“弱哥德巴赫猜想”或“关于奇数的哥德巴赫猜想”。若关于偶数的哥德巴赫猜想是对的,则关于奇数的哥德巴赫猜想也会是对的。

1966年陈景润证明了"1+2"成立,即"任一充分大的偶数都可以表示成二个素数的和,或是一个素数和一个半素数的和"。
2013年5月,巴黎高等师范学院研究员哈洛德·贺欧夫各特发表了两篇论文,宣布彻底证明了弱哥德巴赫猜想。
■网友的回复
2020如何暴富?
■网友的回复
有啊!早上吃什么,中午吃什么,晚上吃什么。看上去并不震撼,实际上却很难解答
■网友的回复
周长为
其中
ArcLength]数学家知道无法精确表示椭圆周长
就定义
其中
是两个参数
当
时,可以简写成
■网友的回复
哥德巴赫猜想、尺规三等分角。
女朋友为什么生气了?
■网友的回复
比如 你是谁?
■网友的回复
她为什么不喜欢你。
■网友的回复
谢邀。
乍一看以为顶多是初一初二的普通证明题
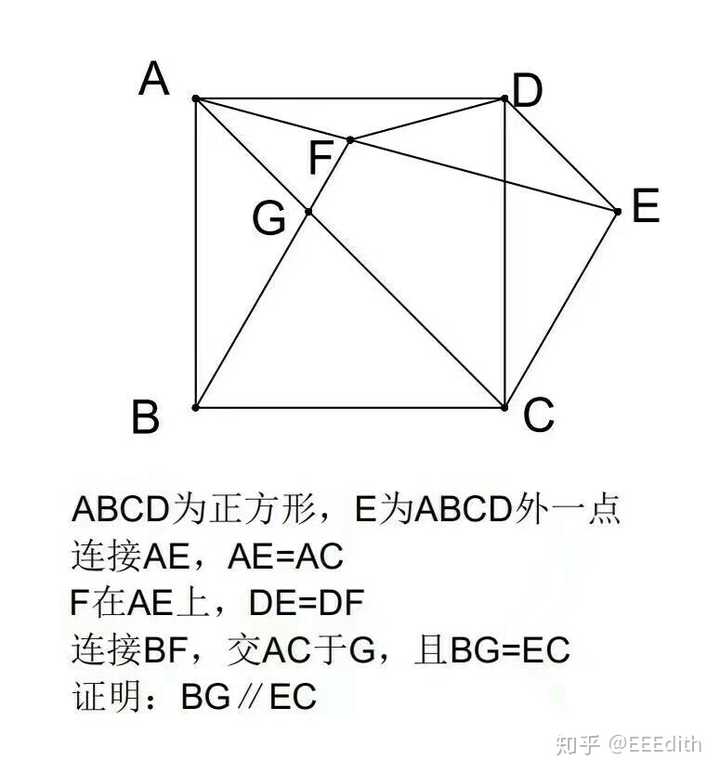
【有哪些一眼看上去并不震撼的问题,实际上很难解答或者根本无法解决】
推荐阅读
- 哪些爱好可以赚钱
- 1000 元以内,有哪些不错的自行车推荐
- 考研去北京的985211,哪些院校不歧视二本
- 申请北理MBA机会大吗 , 北京哪些mba学校可能性比较高
- 北京有哪些提供电视的桌游店
- 去澳大利亚堪培拉旅游,当地有哪些美食,求推荐
- 世界上最好的海洋馆和动物园有哪些
- 暑假去西安哪些地方值得去
- 北京有哪些与近现代相关的历史遗迹?
- 想随脚步了解美国建国史,有哪些必去的历史名迹