NLP:иҜҚдёӯзҡ„ж•°еӯҰ( е…ӯ )
>>> from collections import OrderedDict>>> zero_vector = OrderedDict((token, 0) for token in lexicon)>>> zero_vectorOrderedDict([(',', 0),('.', 0),('and', 0),('as', 0),('faster', 0),('get', 0),('got', 0),('hairy', 0),('harry', 0),('home', 0),('is', 0),('jill', 0),('not', 0),('store', 0),('than', 0),('the', 0),('to', 0),('would', 0)])жҺҘдёӢжқҘеҸҜд»ҘеҜ№дёҠиҝ°еҹәжң¬еҗ‘йҮҸиҝӣиЎҢеӨҚеҲ¶ пјҢ жӣҙж–°жҜҸзҜҮж–ҮжЎЈзҡ„еҗ‘йҮҸеҖј пјҢ 然еҗҺе°Ҷе®ғ们еӯҳеӮЁеҲ°ж•°з»„дёӯпјҡ
>>> import copy>>> doc_vectors = []>>> for doc in docs:...vec = copy.copy(zero_vector)?---copy.copy()жһ„е»әдәҶе®Ңе…ЁзӢ¬з«Ӣзҡ„еүҜжң¬ пјҢ еҚі0еҗ‘йҮҸзҡ„дёҖдёӘзӢ¬з«Ӣзҡ„е®һдҫӢ пјҢ иҖҢйқһеӨҚз”ЁдёҖдёӘжҢҮй’ҲжҢҮеҗ‘еҺҹе§ӢеҜ№иұЎзҡ„еҶ…еӯҳдҪҚзҪ® пјҢ еҗҰеҲҷ пјҢ е°ұдјҡеңЁжҜҸж¬ЎеҫӘзҺҜдёӯз”Ёж–°еҖјйҮҚеҶҷзӣёеҗҢзҡ„zero_vector пјҢ д»ҺиҖҢеҜјиҮҙжҜҸж¬ЎеҫӘзҺҜйғҪжІЎжңүдҪҝз”Ёж–°зҡ„йӣ¶еҗ‘йҮҸ...tokens = tokenizer.tokenize(doc.lower())...token_counts = Counter(tokens)...for key, value in token_counts.items():...vec[key] = value / len(lexicon)...doc_vectors.append(vec)зҺ°еңЁжҜҸзҜҮж–ҮжЎЈеҜ№еә”дёҖдёӘеҗ‘йҮҸ пјҢ жҲ‘们жңү3дёӘеҗ‘йҮҸ гҖӮ йӮЈжҺҘдёӢжқҘжҖҺд№ҲеҠһпјҹжҲ‘们иғҪеҜ№е®ғ们еҒҡдәӣд»Җд№Ҳпјҹе®һйҷ…дёҠ пјҢ иҝҷйҮҢзҡ„ж–ҮжЎЈиҜҚйў‘еҗ‘йҮҸиғҪеӨҹеҒҡд»»ж„Ҹеҗ‘йҮҸиғҪеҒҡзҡ„жүҖжңүжңүи¶Јзҡ„дәӢжғ… пјҢ еӣ жӯӨ пјҢ жҺҘдёӢжқҘжҲ‘们йҰ–е…ҲеӯҰд№ дёҖдәӣжңүе…іеҗ‘йҮҸе’Ңеҗ‘йҮҸз©әй—ҙзҡ„зҹҘиҜҶ[3] гҖӮ
еҗ‘йҮҸз©әй—ҙеҗ‘йҮҸжҳҜзәҝжҖ§д»Јж•°жҲ–еҗ‘йҮҸд»Јж•°зҡ„дё»иҰҒз»„жҲҗйғЁеҲҶ гҖӮ е®ғжҳҜдёҖдёӘжңүеәҸзҡ„ж•°еҖјеҲ—иЎЁ пјҢ жҲ–иҖ…иҜҙиҝҷдәӣж•°еҖјжҳҜеҗ‘йҮҸз©әй—ҙдёӯзҡ„еқҗж Ү гҖӮ е®ғжҸҸиҝ°дәҶз©әй—ҙдёӯзҡ„дёҖдёӘдҪҚзҪ® пјҢ жҲ–иҖ…е®ғд№ҹеҸҜд»Ҙз”ЁжқҘзЎ®е®ҡз©әй—ҙдёӯдёҖдёӘзү№е®ҡзҡ„ж–№еҗ‘е’ҢеӨ§е°ҸжҲ–и·қзҰ» гҖӮ з©әй—ҙпјҲspaceпјүжҳҜжүҖжңүеҸҜиғҪеҮәзҺ°еңЁиҝҷдёӘз©әй—ҙдёӯзҡ„еҗ‘йҮҸзҡ„йӣҶеҗҲ гҖӮ еӣ жӯӨ пјҢ дёӨдёӘеҖјз»„жҲҗзҡ„еҗ‘йҮҸеңЁдәҢз»ҙеҗ‘йҮҸз©әй—ҙдёӯ пјҢ иҖҢ3дёӘеҖјз»„жҲҗзҡ„еҗ‘йҮҸеңЁдёүз»ҙеҗ‘йҮҸз©әй—ҙдёӯ пјҢ д»ҘжӯӨзұ»жҺЁ гҖӮ
дёҖеј дҪңеӣҫзәёжҲ–иҖ…еӣҫеғҸдёӯзҡ„еғҸзҙ зҪ‘ж јйғҪжҳҜеҫҲеҘҪзҡ„дәҢз»ҙеҗ‘йҮҸз©әй—ҙ гҖӮ жҲ‘们еҸҜд»ҘзңӢеҲ°иҝҷдәӣеқҗж ҮйЎәеәҸзҡ„йҮҚиҰҒжҖ§ гҖӮ еҰӮжһңжҠҠдҪңеӣҫзәёдёҠиЎЁзӨәдҪҚзҪ®зҡ„xеқҗж Үе’Ңyеқҗж ҮеҖ’иҪ¬ пјҢ иҖҢдёҚеҖ’иҪ¬жүҖжңүзҡ„еҗ‘йҮҸи®Ўз®— пјҢ йӮЈд№ҲзәҝжҖ§д»Јж•°й—®йўҳзҡ„жүҖжңүзӯ”жЎҲйғҪдјҡзҝ»иҪ¬ гҖӮ з”ұдәҺxеқҗж Үе’Ңyеқҗж Үдә’зӣёжӯЈдәӨ пјҢ еӣ жӯӨдҪңеӣҫзәёе’ҢеӣҫеғҸжҳҜзӣҙзәҝз©әй—ҙжҲ–иҖ…欧еҮ йҮҢеҫ—з©әй—ҙзҡ„дҫӢеӯҗ гҖӮ жҲ‘们еңЁжң¬з« дёӯи®Ёи®әзҡ„еҗ‘йҮҸйғҪжҳҜзӣҙзәҝз©әй—ҙ пјҢ жҲ–иҖ…欧еҮ йҮҢеҫ—з©әй—ҙ гҖӮ
ең°еӣҫжҲ–ең°зҗғд»ӘдёҠзҡ„з»Ҹзә¬еәҰз®—д»Җд№Ҳе‘ўпјҹең°еӣҫжҲ–ең°зҗғд»Әз»қеҜ№жҳҜдёҖдёӘдәҢз»ҙеҗ‘йҮҸз©әй—ҙ пјҢ еӣ дёәе®ғжҳҜз»ҸеәҰе’Ңзә¬еәҰдёӨдёӘж•°еҖјзҡ„жңүеәҸеҲ—иЎЁ гҖӮ дҪҶжҳҜжҜҸдёӘз»Ҹзә¬еәҰеҜ№йғҪжҸҸиҝ°дәҶдёҖдёӘиҝ‘дјјзҗғйқўгҖҒеҮ№еҮёдёҚе№ізҡ„иЎЁйқўпјҲең°зҗғзҡ„иЎЁйқўпјүдёҠзҡ„дёҖдёӘзӮ№ гҖӮ з»Ҹзә¬еәҰеқҗж ҮдёҚжҳҜзІҫзЎ®жӯЈдәӨзҡ„ пјҢ жүҖд»Ҙз»Ҹзә¬еәҰжһ„жҲҗзҡ„еҗ‘йҮҸз©әй—ҙ并дёҚжҳҜзӣҙзәҝз©әй—ҙ гҖӮ иҝҷж„Ҹе‘ізқҖжҲ‘们计算еғҸдәҢз»ҙз»Ҹзә¬еәҰеҗ‘йҮҸдёҖж ·зҡ„еҗ‘йҮҸеҜ№жҲ–иҖ…йқһ欧еҮ йҮҢеҫ—з©әй—ҙдёӢзҡ„еҗ‘йҮҸеҜ№жүҖиЎЁзӨәзҡ„дёӨзӮ№д№Ӣй—ҙзҡ„и·қзҰ»жҲ–зӣёдјјеәҰж—¶ пјҢ еҝ…йЎ»еҚҒеҲҶе°Ҹеҝғ гҖӮ и®ҫжғідёҖдёӢеҰӮдҪ•еҹәдәҺз»Ҹзә¬еәҰеқҗж Үи®Ўз®—жіўзү№е…°е’ҢзәҪзәҰд№Ӣй—ҙзҡ„и·қзҰ»[4] гҖӮ
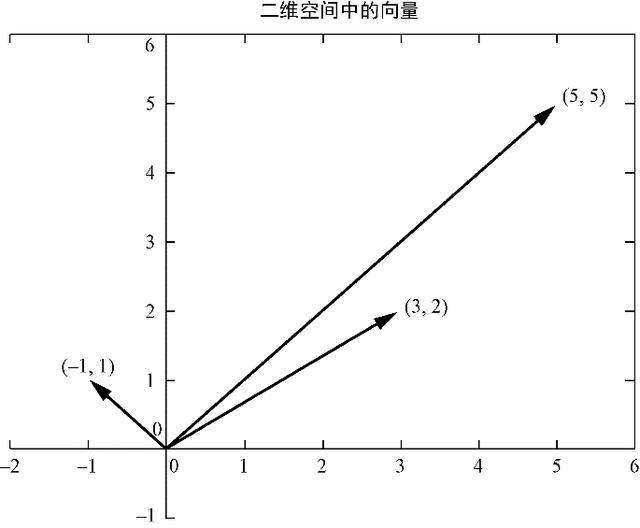
еӣҫ3-1з»ҷеҮәдәҶдәҢз»ҙеҗ‘йҮҸ(5, 5)гҖҒ(3, 2)е’Ң(?1, 1)зҡ„дёҖз§ҚеӣҫзӨәж–№жі• гҖӮ еҗ‘йҮҸзҡ„еӨҙйғЁпјҲз®ӯеӨҙзҡ„е°–пјүз”ЁдәҺиЎЁзӨәеҗ‘йҮҸз©әй—ҙдёӯзҡ„дёҖдёӘдҪҚзҪ® гҖӮ еӣ жӯӨ пјҢ еӣҫдёӯ3дёӘеҗ‘йҮҸзҡ„еӨҙйғЁеҜ№еә”дәҶ3з»„еқҗж Ү гҖӮ дҪҚзҪ®еҗ‘йҮҸзҡ„е°ҫйғЁпјҲжңүеҗ‘зәҝж®өзҡ„е°ҫйғЁпјүжҖ»жҳҜеңЁеқҗж ҮеҺҹзӮ№(0, 0) гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
еӣҫ3-1гҖҖдәҢз»ҙеҗ‘йҮҸ
еҰӮжһңжҳҜдёүз»ҙеҗ‘йҮҸз©әй—ҙеә”иҜҘжҖҺд№ҲеҠһпјҹжҲ‘们з”ҹжҙ»зҡ„дёүз»ҙзү©зҗҶдё–з•Ңдёӯзҡ„дҪҚзҪ®е’ҢйҖҹеәҰеҸҜд»Ҙз”Ёдёүз»ҙеҗ‘йҮҸзҡ„еқҗж ҮxгҖҒyгҖҒzжқҘиЎЁзӨә гҖӮ жҲ–иҖ… пјҢ з”ұжүҖжңүз»ҸеәҰ-зә¬еәҰ-й«ҳеәҰдёүе…ғз»„еҪўжҲҗзҡ„жӣІйқўз©әй—ҙеҸҜд»ҘжҸҸиҝ°иҝ‘ең°зҗғиЎЁйқўзҡ„дҪҚзҪ® гҖӮ
дҪҶжҳҜ пјҢ жҲ‘们дёҚд»…д»…еұҖйҷҗдәҺдёүз»ҙз©әй—ҙ гҖӮ жҲ‘们еҸҜд»Ҙжңү5з»ҙгҖҒ10з»ҙгҖҒ5000з»ҙзӯүеҗ„з§Қз»ҙеәҰзҡ„з©әй—ҙ гҖӮ зәҝжҖ§д»Јж•°еҜ№е®ғ们зҡ„еӨ„зҗҶж–№ејҸйғҪжҳҜдёҖж ·зҡ„ гҖӮ йҡҸзқҖз»ҙж•°зҡ„еўһеҠ пјҢ жҲ‘们еҸҜиғҪйңҖиҰҒжӣҙеҠ ејәеӨ§зҡ„з®—еҠӣ гҖӮ еӨ§е®¶е°ҶдјҡйҒҮеҲ°жүҖи°“зҡ„вҖңз»ҙж•°зҒҫйҡҫвҖқ[5]й—®йўҳ пјҢ дҪҶжҳҜжҲ‘们дјҡеҲ°жңҖеҗҺдёҖз« пјҲеҚіз¬¬13з« пјүеҶҚеӨ„зҗҶиҝҷдёӘй—®йўҳ гҖӮ
жҺЁиҚҗйҳ…иҜ»
- Eyeware BeamдҪҝз”ЁiPhoneиҝҪиёӘзҺ©е®¶еңЁжёёжҲҸдёӯзҡ„зңјзқӣиҝҗеҠЁ
- з”°дјҹйҷўеЈ«пјҡжҲ‘зңјдёӯзҡ„еҢ»з–—жңәеҷЁдәә
- Mozillaе°Ҷй»ҳи®ӨзҰҒз”ЁFirefoxдёӯзҡ„йҖҖж јй”®д»ҘйҳІжӯўз”ЁжҲ·зј–иҫ‘ж•°жҚ®дёўеӨұ
- LG Stylo 7жёІжҹ“еӣҫжӣқе…үпјҡжІЎжңүйў„жғідёӯзҡ„йҮҚеӨ§еҚҮзә§
- е№іж·Ўж— еҘҮдёӯзҡ„жҡ—иҮӘеҚҮзә§пјҢ2020е№ҙдё»жқҝеёӮеңәе№ҙз»ҲзӣҳзӮ№
- жүӢжңәдёӯзҡ„вҖңе“ҲжӣјеҚЎйЎҝвҖқпјҢе°Ҹзұі11еҸҲжңү黑科жҠҖжӣқе…ү
- и°·жӯҢProject ZeroжҠ«йңІдәҶWindowsдёӯзҡ„дёҘйҮҚе®үе…ЁжјҸжҙһ
- еҫ®дҝЎжҺЁеҮәвҖңеҫ®дҝЎиұҶвҖқпјҢеҸҜз”ЁдәҺиҙӯд№°зӣҙж’ӯдёӯзҡ„иҷҡжӢҹзӨјзү©пјҢдҪ дјҡе……еҖјеҗ—пјҹ
- жӣҫжҳҜзӣ—зүҲдёӯзҡ„жҲҗеҠҹжЎҲдҫӢпјҢиҝҳе°ҶжӯЈе“Ғе…¬еҸёж”¶иҙӯпјҢеҺҹеӣ жҳҜвҖңиҝ·еӨұдәҶвҖқж–№еҗ‘
- и°·жӯҢжҠ«йңІеӯҳеңЁдәҺй«ҳйҖҡйӘҒйҫҷAdreno GPUдёӯзҡ„й«ҳеҚұжјҸжҙһ

















