江苏龙网

  1. 首页 > 人文 > >

深度学习入门之第五章：经典卷积神经网络

5.1 LeNet-5
LeNet-5是由有着卷积神经网络之父美誉的Yann LeCun（中文翻译为杨立昆）于1998年提出的一种经典的卷积网络结构 。 它是第一个成功应用于数字识别问题的卷积神经网络 。 在MNIST数据集上 ， LeNet-5模型可以达到大约99.2%的正确率 。 作为早期的一种卷积神经网络结构 ， LeNet-5的提出极大地推动了后续卷积神经网络的发展 ， 它通常被认为是CNN的开山之作 。
5.1.1
LeNet-5网络结构
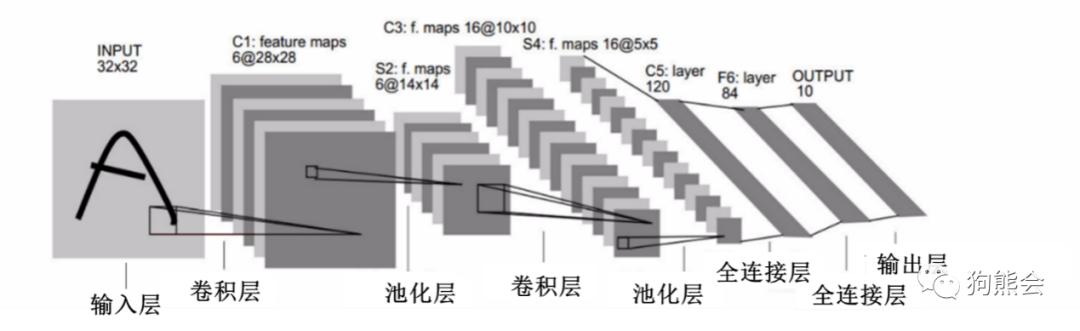
首先介绍LeNet-5的网络结构 ， 如果输入层不计入层数 ， 则LeNet-5总共有7层网络 ， 网络结构如图5.1所示 。
深度学习入门之第五章：经典卷积神经网络文章插图
图5.1 LeNet-5网络结构
从图5.1可以看出 ， LeNet-5总共由输入层、卷积层、池化层、卷积层、池化层、全连接层、全连接层、输出层组成 。 下面详细介绍每一层的结构 。
（1）输入层 。 一张32×32的灰度图像 ， 只有一个颜色通道 。
（2）卷积层 。 将输入与6个高为5 ， 宽为5 ， 深度为1的卷积核进行valid卷积 ， 由于输入是灰度图 ， 所以卷积核的深度也是1 ， 又由于是valid卷积 ， 所以卷积后的结果为 ， 高为28（32-5+1） ， 宽为28（32-5+1） ， 深度为6（因为用了6个卷积核） 。
（3）池化层 。 对（2）中卷积层输出的28×28×6的抽象矩阵进行valid最大值池化操作 ， 使用6个2×2大小的矩阵进行valid最大值池化处理 ， 池化层的输出结果为14×14×6的矩阵 。
（4）卷积层 。 将（3）中池化层的输出与16个大小为5×5×6的卷积核进行valid卷积 ， 输出结果为10×10×16 。
（5）池化层 。 同第（3）步一样 ， 对（4）的输出结果进行valid最大值池化的操作 ， 输出矩阵的维度为5×5×16 。
（6）全连接层 。 将第（5）步输出的矩阵拉直成一维向量 ， 这个向量的长度为5×5×16=400 ， 将该向量经过一个全连接神经网络处理 ， 该全连接神经网络共有2个隐含层 ， 其中输入层有400个神经元 ， 第1个隐含层有120个神经元 ， 第2个隐含层有84个神经元 。
（7）输出层 。 因为LeNet-5最初是用来识别手写数字 ， 处理的是0～9的10分类问题 ， 所以它的输出层有10个神经元 。
以上就是LeNet-5的模型结构 ， LeNet-5无论是在网络结构 ， 还是在参数规模上 ， 都相对简单 。 接下来通过手写数字识别这个经典案例具体讲解LeNet-5的代码实现 。
5.1.2
案例：LeNet-5手写数字识别
下面通过经典的手写数字识别分类问题介绍LeNet-5的代码实现 。
01
MNIST数据集展示
MNIST数据集在前面已经详细介绍过 ， 该案例的目的是区分0～9这10个数字 。 在Keras框架下 ， 可以通过mnist.load_data()函数加载数据集 。 TensorFlow已经将数据集准备好并且做了区分 。 例如这里的（X0,Y0）是训练集 ， （X1,Y1）是测试集 。 将X0打印出来 ， 可以看到这是一个6万行的立体矩阵 ， 每个矩阵都代表一张图像 ， 其中每张图像的像素矩阵是28×28 。
需要注意的是 ， LeNet-5第一次被提出来时要求输入是32×32 ， 但是这个数据集的输入是28×28 ， 这并不影响对模型的应用 。 通过pyplot函数可以将训练集中0～9这10个数字展示出来 。 具体如代码示例5-1所示 。
代码示例5-1：加载数据并展示
1from Keras.datasets import mnist 2(X0,Y0),(X1,Y1) = mnist.load_data() 3print(X0.shape) 4from matplotlib import pyplot as plt 5plt.figure() 6fig,ax = plt.subplots(2,5) 7ax=ax.flatten() 8for i in range(10): 9Im=X0[Y0==i][0]10ax[i].imshow(Im)11plt.show();输出：
1(60000, 28, 28)
深度学习入门之第五章：经典卷积神经网络文章插图


推荐阅读


上一篇：互联网老司机怒敲黑板：这五点都做不到，还赚什么一千万？

下一篇：Linux 通过/dev/uinput模拟按键发送Key键值