еҲқдёӯж•°еӯҰ|дёҖйҒ“зҫҺеӣҪеҲқдёӯж•°еӯҰз«һиөӣйўҳпјҡжұӮйҳҙеҪұйғЁеҲҶйқўз§ҜпјҢе°ҸеӯҰз”ҹзңӢе®Ңзӣҙе‘јз®ҖеҚ•
гҖҗеҲқдёӯж•°еӯҰ|дёҖйҒ“зҫҺеӣҪеҲқдёӯж•°еӯҰз«һиөӣйўҳпјҡжұӮйҳҙеҪұйғЁеҲҶйқўз§ҜпјҢе°ҸеӯҰз”ҹзңӢе®Ңзӣҙе‘јз®ҖеҚ•гҖ‘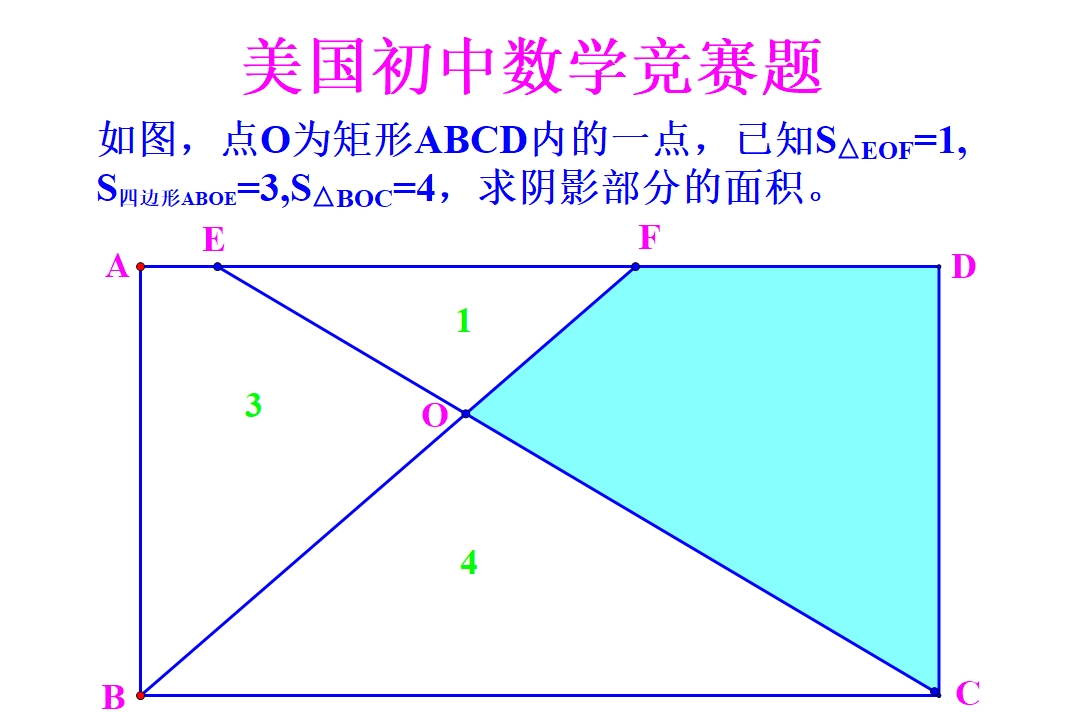
ж–Үз« еӣҫзүҮ
ж–Үз« еӣҫзүҮ

еӨ§е®¶еҘҪ пјҢ д»ҠеӨ©е’ҢеӨ§е®¶еҲҶдә«дёҖйҒ“зҫҺеӣҪеҲқдёӯж•°еӯҰз«һиөӣйўҳпјҡжұӮйҳҙеҪұйғЁеҲҶзҡ„йқўз§Ҝ гҖӮ иҝҷйҒ“йўҳзӣ®зңӢдјјеҫҲйҡҫ пјҢ дҪҶжҳҜжғіжҳҺзҷҪе…¶дёӯзҡ„е…ій”®зӮ№еҗҺ пјҢ е°ұиҝһдёҠиҝҮеҘҘж•°зҡ„е°ҸеӯҰз”ҹйғҪиЎЁзӨәйқһеёёз®ҖеҚ• гҖӮ йӮЈд№Ҳ究з«ҹжҳҜдёҖйҒ“д»Җд№Ҳж ·зҡ„йўҳзӣ®е‘ўпјҹдёӢйқўжҲ‘们дёҖиө·жқҘзңӢдёҖдёӢ гҖӮ
йўҳзӣ®пјҡеҰӮеӣҫ пјҢ еӣӣиҫ№еҪўABCDдёәзҹ©еҪў пјҢ зӮ№EгҖҒFдёәиҫ№ADдёҠзҡ„дёӨзӮ№ пјҢ иҝһжҺҘBFе’ҢCEзӣёдәӨдәҺзӮ№O гҖӮ е·ІзҹҘдёүи§’еҪўEOFзҡ„йқўз§Ҝдёә1 пјҢ еӣӣиҫ№еҪўABOEзҡ„йқўз§Ҝдёә3 пјҢ дёүи§’еҪўBOCзҡ„йқўз§Ҝдёә4 пјҢ жұӮйҳҙеҪұйғЁеҲҶзҡ„йқўз§Ҝ гҖӮ
еӣҫдёӯйҳҙеҪұйғЁеҲҶжҳҜдёҖдёӘдёҚ规еҲҷзҡ„еӣӣиҫ№еҪў пјҢ иҰҒзӣҙжҺҘжұӮи§Јжҳҫ然жҜ”иҫғеӣ°йҡҫ гҖӮ жұӮи§Јиҝҷз§ҚеӣҫеҪўйқўз§Ҝзҡ„дёҖиҲ¬жҖқи·ҜжңүдёӨз§ҚпјҡдёҖжҳҜйҖҡиҝҮеҒҡиҫ…еҠ©зәҝе°Ҷеӣӣиҫ№еҪўеҲҶжҲҗдёӨдёӘдёүи§’еҪўпјӣдәҢжҳҜе°ҶжүҖжұӮеӣӣиҫ№еҪўж”ҫеңЁеҸҰеӨ–дёҖдёӘеӨ§зҡ„еӣҫеҪўдёӯ пјҢ 然еҗҺз”ЁеӨ§еӣҫеҪўзҡ„йқўз§ҜеҮҸеҺ»е…¶д»–йғЁеҲҶзҡ„йқўз§ҜеҚіеҸҜ гҖӮ
е…ҲжқҘзңӢжҖқи·ҜдёҖ гҖӮ ж— и®әжҳҜиҝһжҺҘCFиҝҳжҳҜODйғҪеҸҜд»Ҙе°ҶйҳҙеҪұйғЁеҲҶеҲҶжҲҗ2дёӘдёүи§’еҪў пјҢ дҪҶжҳҜеҲҶеҮәжқҘзҡ„2дёӘдёүи§’еҪўзҡ„йқўз§ҜйғҪеҫҲйҡҫи®Ўз®—еҮәжқҘ гҖӮ жүҖд»ҘиҝҷдёӘжҖқи·ҜиЎҢдёҚйҖҡдәҶ гҖӮ
еҶҚжқҘзңӢжҖқи·ҜдәҢ гҖӮ жҜ”иҫғе®№жҳ“жғіеҲ°зҡ„е°ұжҳҜе°ҶйҳҙеҪұйғЁеҲҶж”ҫе…Ҙдёүи§’еҪўCDEжҲ–иҖ…зӣҙи§’жўҜеҪўBCDFдёӯ пјҢ дҪҶжҳҜдёүи§’еҪўCDEе’Ңзӣҙи§’жўҜеҪўBCDFзҡ„йқўз§Ҝд№ҹдёҚеҘҪи®Ўз®— гҖӮ йӮЈд№ҲеҶҚжҚўдёӘи§’еәҰ пјҢ е°ҶйҳҙеҪұйғЁеҲҶж”ҫеҲ°зҹ©еҪўABCDдёӯе‘ўпјҹеҰӮжӯӨдёҖжқҘ пјҢ йҳҙеҪұйғЁеҲҶзҡ„йқўз§Ҝе°ұзӯүдәҺзҹ©еҪўйқўз§ҜеҮҸеҺ»еҸҰеӨ–дёүйғЁеҲҶзҡ„йқўз§Ҝ гҖӮ
жҲ‘们е…ҲжқҘзңӢдёҖдёӢеҲ©з”ЁеҲқдёӯзҹҘиҜҶжұӮи§Ј гҖӮ
зҹ©еҪўзҡ„еҜ№иҫ№е№іиЎҢ пјҢ жүҖд»ҘBC//EF пјҢ жүҖд»Ҙдёүи§’еҪўBOCзӣёдјјдәҺдёүи§’еҪўFOE(зӣёдјјдёүи§’еҪўзҡ„вҖңXвҖқжЁЎеһӢ) гҖӮ еӣ дёәдёүи§’еҪўBOCзҡ„йқўз§Ҝдёә4 пјҢ дёүи§’еҪўEOFзҡ„йқўз§Ҝдёә1 пјҢ жүҖд»ҘиҝҷдёӨдёӘдёүи§’еҪўзҡ„зӣёдјјжҜ”дёә2пјҡ1 гҖӮ жүҖд»ҘBC=2EF пјҢ дё”дёүи§’еҪўBOCдёӯиҫ№BCдёҠзҡ„й«ҳд№ҹжҳҜдёүи§’еҪўEOFдёӯиҫ№EFдёҠзҡ„й«ҳзҡ„2еҖҚ гҖӮ
и®ҫEF=x пјҢ дёүи§’еҪўEOFиҫ№EFдёҠзҡ„й«ҳдёәy пјҢ еҲҷдёүи§’еҪўEOFзҡ„йқўз§Ҝдёәxy/2=1 пјҢ еҚіxy=2 гҖӮ жүҖд»Ҙзҹ©еҪўABCDзҡ„йқўз§Ҝдёә2x*3y=6xy=12 пјҢ 然еҗҺеҶҚеҮҸеҺ»еҸҰеӨ–3йғЁеҲҶзҡ„йқўз§Ҝе°ұжҳҜйҳҙеҪұйғЁеҲҶзҡ„йқўз§ҜдәҶ гҖӮ иҜҰз»ҶиҝҮзЁӢи§ҒдёӢеӣҫ гҖӮ
з”ЁеҲқдёӯзҹҘиҜҶжұӮи§Јжң¬йўҳ пјҢ йҡҫеәҰд№ҹдёҚеӨ§ гҖӮ дёҚиҝҮз”Ёе°ҸеӯҰзҡ„зҹҘиҜҶжқҘи§ЈиҝҳдјҡжӣҙеҠ з®ҖеҚ• пјҢ з”ҡиҮіеҸҜд»ҘеҸЈз®—еҫ—еҮәзӯ”жЎҲ гҖӮ
иҝһжҺҘBEе’ҢCF пјҢ йӮЈд№ҲеңЁжўҜеҪўBCFEдёӯе°ұеҮәзҺ°дәҶдёҖдёӘиқҙиқ¶жЁЎеһӢ гҖӮ жўҜеҪўдёӯзҡ„иқҙиқ¶жЁЎеһӢжңүдёӨдёӘйҮҚиҰҒз»“и®әпјҡдёҖжҳҜдёӨзҝ…иҶҖдёүи§’еҪўзҡ„йқўз§Ҝзӣёзӯү пјҢ еҚідёүи§’еҪўBOEе’Ңдёүи§’еҪўCOFпјӣдәҢжҳҜеӨҙе°ҫдёӨдёүи§’еҪўзҡ„йқўз§Ҝд№Ӣз§ҜзӯүдәҺдёӨзҝ…иҶҖдёүи§’еҪўзҡ„йқўз§Ҝд№Ӣз§Ҝ пјҢ еҚідёүи§’еҪўEOFе’ҢBOCзҡ„йқўз§Ҝд№Ӣз§ҜзӯүдәҺдёүи§’еҪўBOEе’ҢCOFйқўз§Ҝд№Ӣз§Ҝ гҖӮ иҝҷж ·е°ұеҸҜд»ҘжұӮеҮәдёүи§’еҪўCOFзҡ„йқўз§Ҝ пјҢ д»ҺиҖҢжұӮеҮәдёүи§’еҪўACFзҡ„йқўз§Ҝе’Ңзҹ©еҪўйқўз§Ҝ гҖӮ
еҜ№жҜ”дёҖдёӢдёӨз§Қи§Јжі• пјҢ еҫҲжҳҺжҳҫз”Ёе°ҸеӯҰзҡ„иқҙиқ¶жЁЎеһӢжӣҙеҠ з®ҖеҚ• пјҢ з”ҡиҮідёҚз”ЁеҠЁз¬”д№ҹиғҪи®Ўз®—еҮәз»“жһң пјҢ жүҖд»Ҙжңүе°ҸеӯҰз”ҹзӣҙе‘јиҝҷйҒ“йўҳеӨӘз®ҖеҚ•дәҶ гҖӮ дҪ и§үеҫ—е‘ўпјҹ
жҺЁиҚҗйҳ…иҜ»
- ж•°еӯҰ|дҪ и§ҒиҝҮжңҖи®ҪеҲәзҡ„дәӢжҳҜд»Җд№ҲпјҹдҝЎеҝғж»Ўж»ЎжҠҠиҜ•еҚ·з»ҷжҲ‘жҠ„жҲҗеҖ’数第дәҢпјҒ
- ж•°еӯҰ|дәӢдёҡеҚ•дҪҚеҸҲж¶Ёе·Ҙиө„пјҹйҷӨдәҶе®ғпјҢиҝҷиЎҢд№ҹжҲҗвҖңйҰҷйҘҪйҘҪвҖқпјҢе·Ҙиө„дёҚиҫ“е…¬еҠЎе‘ҳ
- ж•°еӯҰ|жҲ‘们дёҖдёӘиў«вҖңе«ҢејғвҖқдәҶ23е№ҙзҡ„ж•°еӯҰеӨ©жүҚпјҢзҙҜжӯ»жүҚзҹҘйҒ“д»–зҡ„д»·еҖј
- еӣӣе·қзңҒ|еӣӣе·қеҫ·йҳіпјҡжҹҗд№Ўй•ҮеҲқдёӯејҖеӯҰпјҢ家й•ҝеҮ д№ҺиҮӘеёҰеәҠжқҝпјҢеӯҰж Ўз”Ёе“ҒйўқеӨ–收й’ұ
- й’ұй’ҹд№Ұ|д»–й«ҳиҖғж•°еӯҰд»…жңү15еҲҶпјҢж Ўй•ҝеӨҚжҹҘиҜ•еҚ·еҗҺеҚҒеҲҶжҝҖеҠЁпјҢйҒ“пјҡе°ұд»–дәҶ
- ж—©жҒӢ|еҲқдёӯж—¶пјҢиҝҷ4зұ»еҘіз”ҹеҫҲеҸ—з”·з”ҹе–ңж¬ўпјҢжӣҙе®№жҳ“вҖңж—©жҒӢвҖқпјҢиҖҒеёҲпјҡжӢҰдёҚдҪҸ
- иҖғиҜ•|еҲқдёӯеҢ–еӯҰзҹҘиҜҶжЎҶжһ¶еӣҫпјҢеё®еӯ©еӯҗиҙҙеўҷдёҠи®°пјҢдҝқз®ЎиҖғиҜ•ж¬Ўж¬ЎжӢҝж»ЎеҲҶпјҒ
- ж•°еӯҰ|жҲ‘еӣҪвҖңжңҖйҡҫиҖғвҖқзҡ„10жүҖзҗҶе·ҘеӨ§еӯҰпјҢеҪ•еҸ–еҲҶи¶…600еҲҶпјҢеӯҰйңёпјҡдёҚеңЁиҜқдёӢ
- ж•°еӯҰ|ж•°еӯҰйўҳпјҡдёҖдёӘеӣӣдҪҚж•°дёҺе®ғзҡ„еҗ„дёӘдҪҚдёҠзҡ„ж•°д№Ӣе’ҢжҳҜ1972пјҢжұӮиҝҷдёӘеӣӣдҪҚж•°
- дёӯе°ҸеӯҰ|еҲқдёӯж—¶еҗҢеӯҰ家йҮҢеҮ дёӘдәҝпјҢзҸӯйҮҢзҡ„зҸӯиҙ№иў«еҒ·дәҶпјҢиҖҒеёҲ们еҶӨжһүд»–еҒ·зҸӯиҙ№пјҒ











