高考|教育还是严肃些好,希望少些为了博眼球而故意的浮夸,多些实在
文章图片
文章图片
当我看到下面这个标题默默地笑了的时候 , 我已经很多次在首页上看到类似这样的标题了:“为什么以前的初中数学题 , 现在成为高中难题?”无论是以初中数学的角度 , 还是以高中数学的角度来看 , 都是很简单很基础的题 , 为什么就一定要故意说成难题呢?唬小孩儿?上演“狼来啦”?
直截了当 , 上菜 , 哦 , 不是 , 上题 , 顺便给大家复习一点中学数学的基础知识 。
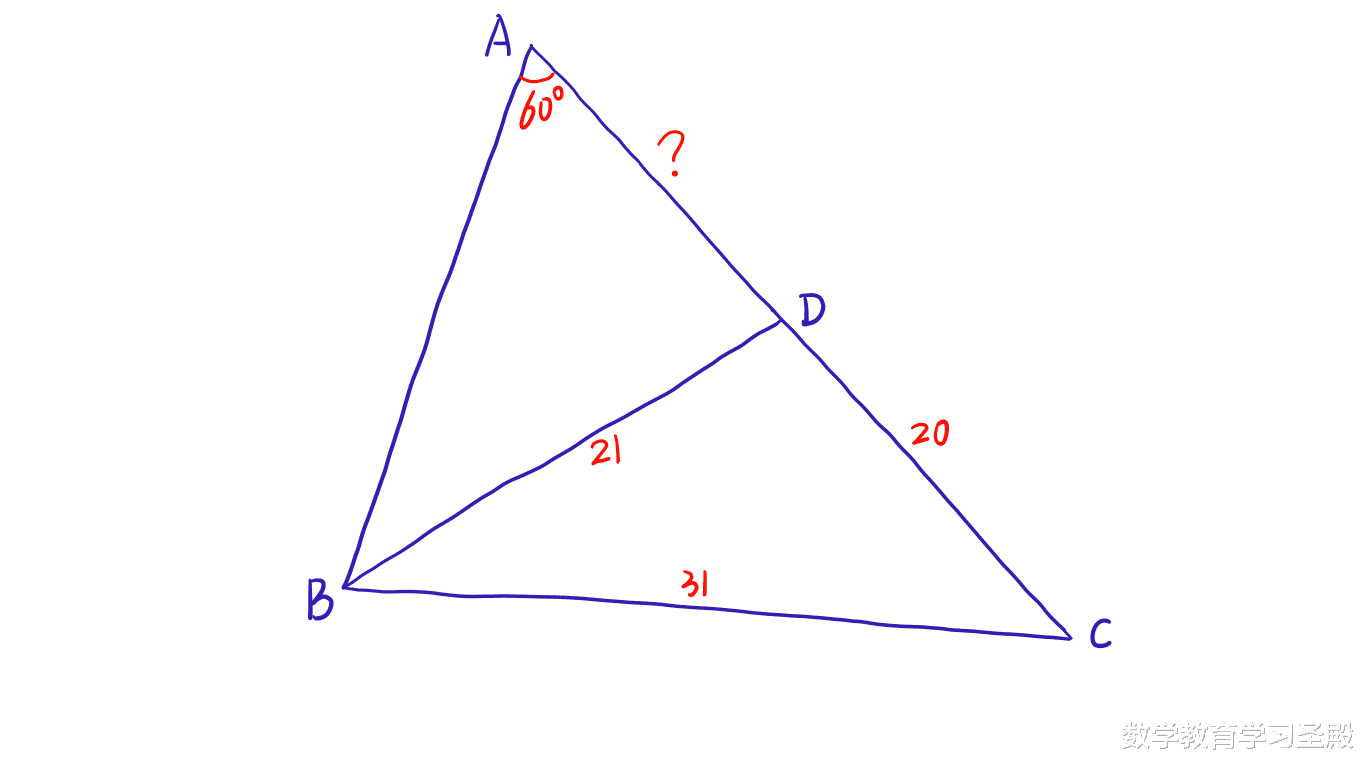
一、题目初中数学高中数学皆可用三角形ABC中 , ∠A=60° , 点D在边AC上 , BC=31 , BD=21 , CD=20 , 则AD的长度为____.
二、思路分析1、高中的思路
①三角形BCD中 , 由余弦定理 , 可得cos∠BDC 。
②三角函数公式 , 结合三角形中角的代换 , 可得sin∠ABD 。
③三角形ABD中 , 由正弦定理 , 即可得AD , 毕.
对于高中数学来说 , 它可以作为三角函数章节的一道基础练习题 , 可以达到练习三角函数的两个基本定理、一个基本公式 , 即余弦定理、正弦定理、正弦差角公式的基本运用的目的 。 但是绝对不是什么所谓的难题 , 大家心中一定要有数 。
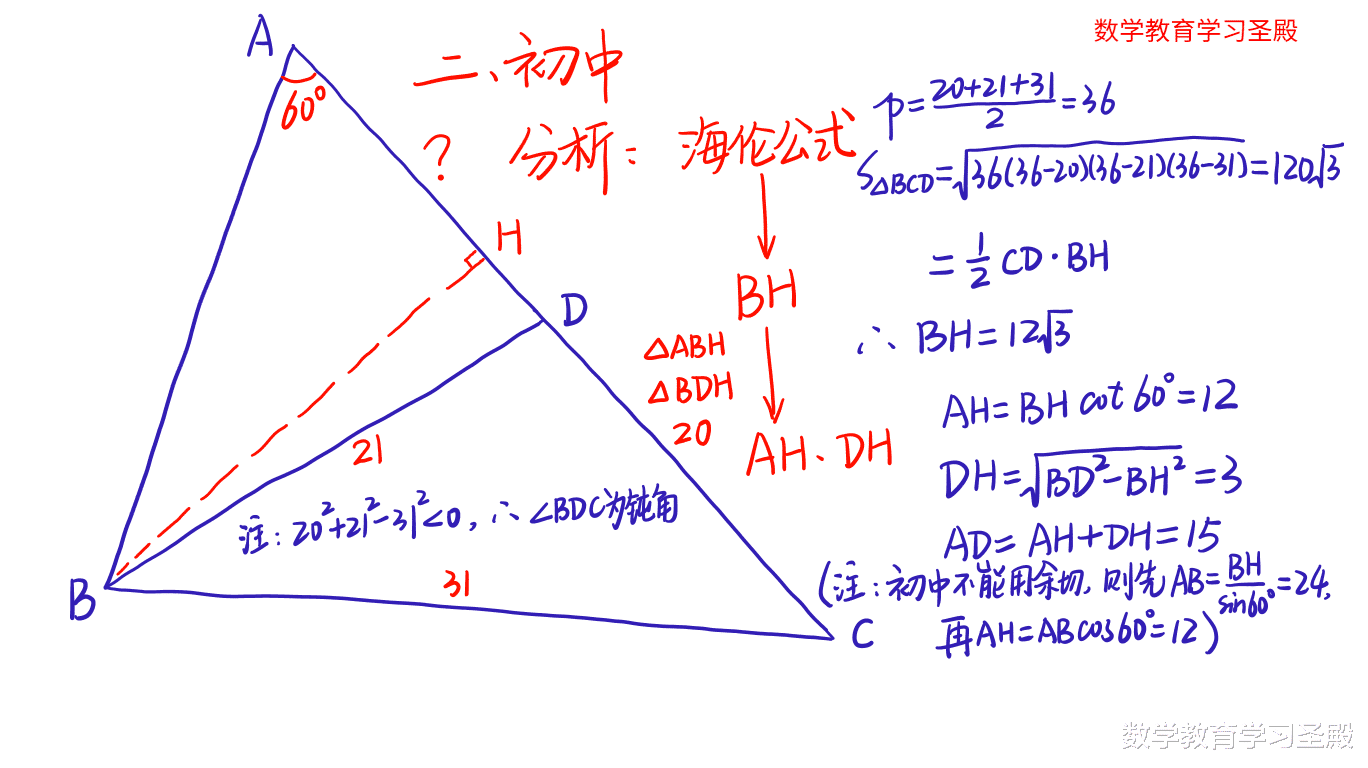
2、初中的思路
①三角形面积公式的运用:
三角形BCD中 , 三条边的长度都已经知道 , 由海伦公式 , 得到它的面积;
【高考|教育还是严肃些好,希望少些为了博眼球而故意的浮夸,多些实在】结合三角形底乘以高除以二的面积公式 , 可得三角形BCD的边CD上的高BH的长度 。
(注:BD平方+CD平方-BC平方<0 , 故∠BDC为钝角 。 )
②直角三角形的运用:
特殊直角三角形ABH中 , 由BH的长度、∠A=60° , 易得AH的长度 。
直角三角形BDH中 , 由勾股定理 , 得到DH的长度 。
AD=AH+DH , 毕 。
当然 , 初中的方法 , 还可以以BH的长度为桥梁 , 在直角三角形BCH、直角三角形BDH中分别运用勾股定理 , 解得DH , 再直角三角形BDH中由勾股定理得BH , 同上得AH , AD=AH+DH , 毕 。
作为初中数学练习题 , 用的也是最基础的知识点 , 也没有什么特别需要综合的地方 , 作为基础练习题尚合适 。
三、网络很多浮夸 , 不可信以为真1、2019年高考数学全国卷一的“断臂维纳斯” , 数学卷刚考完 , 网络媒体就铺天盖地的吹来吹去 , 不断发酵 , 说有多么地为难考生 。 当然也确实有考生被唬住了 , 也有考生“投机取巧”就得了分 。 而实际上它只是一道比例、大小范围题 , 管你黄金分割比例还是别的什么比例 , 你就是一个比例 。 讲完了“断臂维纳斯” , 题又不关维纳斯的事 , 一定不能被唬住啊 , 尤其是以后的高考考生遇到类似的题 。
2、2020年高考数学全国卷一的“金字塔” , 同样是数学卷刚考完 , 网络媒体就借“高考金字塔”迅速发酵 , 居然还迅速冲上热搜 。
金字塔只是说着玩的 , 它的本质就是正四棱锥的高为边长的正方形的面积作为中间桥梁 , 联结勾股定理 , 和侧面三角形的面积 , 转化为解一元二次方程即可 。 稍微有点空间思维能力即可 。
教育还是严肃些好 , 希望少些为了博眼球而故意的浮夸 , 少些类似为了借着“高考”的“东风”上热搜的无尽发酵 , 多些实实在在的本真 。
推荐阅读
- 香港大学|即使高考失利上专科,也可以专升本,但3这点要注意,收藏备用
- 作文|如何正确看待,张子枫的高考事件?很多人都是断章取义吗?
- 郑强|当初那个认为科学有国界,要取消英语高考的郑强,现再怎样了
- |大一新生报到,“被子”是自己带好还是去学校买好?学姐来告诉你
- |爸爸让弟弟帮忙念哥哥的高考成绩,只得了51分,哥哥开始坐不住了
- 书法|高考状元唐楚玥写的字,网友直夸“神仙字体”:难怪语文考146分
- |高考史上“年龄最小”的神童,11岁考上985大学,今现状如何?
- 易烊千玺|明星高考成绩:关晓彤552、易烊千玺473,都不如681的她!
- 杏鲍菇|高考后,娘俩的极简午餐,一周不重样,网友:没有对比就没有伤害
- 张子枫|张子枫疑似学霸人设翻车,高考分数出来,或将无缘北电














